���Ђ̋Ɩ��Ŏg�p���Ă���p���������Ă��܂��D
Home�@���������@��ЊT�v�@�A�s�@�J�s�@�T�s�@�^�s�@�i�s�@�n�s�@�}�s�@���s�@���s�@���s�@�Q�l����
��P��̌��i���v�I��������C�댯���C�L�Ӑ����ȂǎQ�Ɓj
���v�I��������́C�N���������ۂ����R���ۂ��ׂ���@�ł��邪�C���_�͋��R�ł���\�����m���ɂ���ĕ\������D���Ȃ킿�C���R�ɋN�������\�����P���ȉ��ł��邩����R�Ƃ͍l���Ȃ������Ó��ł���C�Ƃ����悤�Ȍ��_�̏o����������D���������āC���R�ł͂Ȃ��ƌ��_���o���Ă��C���R�ɋN�������\���̓[���ł͂Ȃ��C�ɂ��܂�Ȏ��ۂ��N��������������Ȃ��D�펯�ł͍l�����Ȃ��悤�Ȏ��ۂ��N�������Ƃ��ɂ͌��_�����ɂȂ�D���̂悤�Ȍ����P��̌��Ƃ����D���v�I�ȉ������������ꍇ�C�O�����ċ��e�������̑傫�������߂�D���̈Ӗ��Ŋ댯���Ƃ�������D�ǂ̂��炢�̊����܂ŋ��e����̂��ƌ����Ӗ��ł́C�L�Ӑ����Ƃ������Ă���D
�Ή��̂��邔����i���v�I��������C������ȂǎQ�Ɓj
�u�Ή��̂���v�Ƃ́C����̑Ώۂ�������ς��ĂQ�x���肳�ꂽ�Ƃ��C���邢�͉��炩�̏����ɂ���đ��肪�Ή��t����ꂽ�ꍇ�������D�����C�N��ȂǑΏۂ̃����o�[���قȂ�ꍇ�ɂ́u�Ή����Ȃ��v���ƂɂȂ�D����̃T���v�����Q�肳�ꂽ�Ƃ��̕��ϒl�̍������肷��Ƃ��ɂ͑Ή��̂��邔������s���������o�͂������Ȃ�D�w�K�̌��ʂȂǓ����l�ɑ���Q�x�̃e�X�g�̍������肷��Ƃ��Ȃǂ͑Ή��̂��錟�������D�قȂ����Q�̕��ς̍��͑Ή��̂Ȃ��������p����D�����ɂ����āC���ڊԂ̍��̌���́u�Ή��̂��錟��v��p���āC�����C�N��̂悤�ɈقȂ����l�̊Ԃ̍��̌���ɂ́C�Ή��̂Ȃ������肩�P�v���̕��U���͂�p����D�Ή��̂��邔����͂Q�̐��l�̍��̃[������Ɠ����ł���D�܂��C�Q�v���̕Е��̗v�����ʂ��l�����āC���U�����邪�C���̗v�������肵�Ȃ����Ƃ��Ӗ�����D
�Ή��̂����̍��̌���i���v�I��������Q�Ɓj
�u�Ή��̂���v�Ƃ́C����̑Ώۂ�������ς��ĂQ�x���肳�ꂽ�Ƃ��ɗp������D�Q�x�̑���l���䗦�ŕ\�������Ƃ��C�Ή��̂����̌���@��p����D
�ΐ��I�b�Y�i�I�b�Y�C�I�b�Y��Q�Ɓj
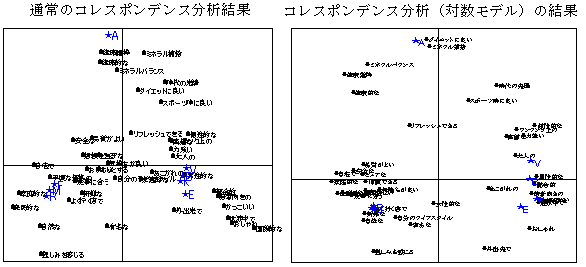
�I�b�Y�̑ΐ����Ƃ������́Dy=log�op/(1-p)�p(0<p<1)�ŕ\�킳���D���W�b�g�ϊ����ƈ�v����D�I�b�Y��ΐ��ϊ�����ƁC���W�X�e�B�b�N���Ɛ��`�I�ȊW�ɂȂ�D�I�b�Y�́C�q�̏ɂ����āC�m�����s�����ǂ����Ƃ������D�P���傫����Γ�����̉\���������C�P��菬������͂����\���������Ȃ�D������m�����P�ɋ߂��Ȃ�ƁC���Ȃ�傫�ȓx���Ŋ|����̂ŁC�P�Ȃ�I�b�Y�ł́C�S���I�Ȋ��҂�댯�x���C�ړx�l�Ƃ��ĕ\���ł��Ȃ��D�ΐ����Ƃ�Ɣ�r�I���܂��\���ł���D�䗦�ƐS���I�Ȋ��ғx�i�v���X�����j��댯�x�i�}�C�i�X�����j�Ƃ̊W��\�����̂����W�X�e�B�b�N���ł���i���W�X�e�B�b�N���̐}�Q�Ɓj�D�䗦�́C�S�̂̑傫���ɑ���Y������Ώۂ̑傫���̊����ł��邪�C�傫����ΐ��ϊ����邱�Ƃ��l�Ԃ̃C���[�W�ɂ悭�����Ȃ�C�䗦�́C�S�̓x���̑ΐ��ƊY���x���̑ΐ��̍��ɂ���ĕ\���ł���i�䗦�͐S���ړx��̍��j�D����ɁC������̗��Ƃ͂���̗����C���[�W�I�ɔ�r���邱�Ƃ́C������̐S���ړx�l�i�S�̓x���Ƃ̑ΐ���̍��j�ƁC�͂���̐S���ړx�l�̍����Ƃ�悢���ƂɂȂ�D�I�b�Y�̑ΐ����Ƃ����ΐ��I�b�Y�́C��L�̂悤�ȍs�����f���̕\���Ƃ��ė����ł���D���W�X�e�B�b�N���͐S���ړx�Ƃ͕ʂɁC�䗦�ƐS���ړx�i���ݕϐ��j�Ƃ̊W�����I�ɕ\�������̂Ƃ������߂��ł���D�ΐ��I�b�Y�́C�W�v�\�̏o�����i���z���錻�ہj�Ȃǂɂ悭���p����C���v�I�ɏd�v�ȊT�O�ƂȂ��Ă���D
�ΐ���
y=log x�D�ΐ������������Ƒo�Ȑ����ɂȂ邱�Ƃ���C�ٕ�臂��قڎh���̋t���ɔ�Ⴗ�邱�ƂƊ֘A�Â����āC�h���l���犴�o�l�ւ̕ϊ����i�S���������j�Ƃ��ė��p����Ă����i�t�F�q�i�[�̑ΐ��@���j�D�f�V�x���\���ȂǑΐ��ϊ��́C�S���I�ȗʂ��ߎ��I�ɕ\������̂ɕ֗��ł��邪�C�����ɂ́C�K�������ΐ��������Ă͂܂�킯�ł͂Ȃ��D
�ΐ��Ȑ��̉��p�I�Ӗ�
�����ɐl�Ԃ̍s���⌻�ۂ���舵���ꍇ�C���R�ȑ���l�ɂ̓}�C�i�X���Ȃ��̂����ʂł���D�x���C�����C�傫���ȂǁD���l�ɈӖ���t�����Ƃ��C�}�C�i�X��������D�܂��C�u10�������v�ƌ����悤�ɁC��̑傫�����l�������ɁC�����̑傫���ŗ������邱�Ƃ������D���̂悤�Ȃ��Ƃ́C���z�Ȃǂ̃C���[�W���C�����ł͂Ȃ��C�w���i���ɕt�������l�j�̒��ōl���Ă��邱�ƂɂȂ�D�w���̒��ōl���邱�Ƃ́C�����ɋ߂����l����r�I�ȒP�ɃC���[�W�̒��Ɏ�荞��ŁC�v�l�\�ɂ��Ă���D���̔��ʁC�G�l���M�[���x���̐��ʂ���舵���Ƃ��Ɍ�����Ă��܂����ƂɂȂ�i�w�����x���̑����Z�������ɂ͊|���Z�ɂȂ��Ă��邱�Ɓj�D�܂��C���������ہi�a�C�Ȃǁj�����āC���O�Ɏ��łꍇ�ȂǁC�ɂ߂ď��������l�i�l���ɑ���o�����j��L���Ɏ�舵���Ƃ��ɁC�傫�Ȑ��l�����܂����������̂Ɠ��l�ɁC�l�Ԃ́C�����Ȑ��l�������Ȃ��C���[�W�Ɏ�荞��Ō��ۂ�c�����Ă���D�ΐ����́C���̂悤�ȃv���X�C�傫�����l�C���������l��1�̊��Ŏ�舵����̂ŁC�l�Ԃ̃C���[�W���悭�\���ł��郂�f���ł���D�ΐ����������̐��l����C���[�W�ɍ����ړx�ւ̕ϊ����Ӗ�����Ȃ�C���̋t���ł���w�����̓C���[�W�ɋ߂����l�i�ӎ����x���̑���l�⌻�ہj���G�l���M�[���x���̑���I���ʂɕϊ����郂�f���ƌ�����D�w���^���z�ɂ�������`�\���ȂǁC�w���̒��Ő��I��������邱�Ƃ́C�v���̈Ӗ����l�Ԃ̈ӎ����e�ɋ߂��`�Œ�`����Ă���Ǝv���邱�Ƃ���C��L�̂悤�ȍl�����Ɩ������Ȃ��i�ړx�l�̖��j�D����ɉ����āC�l�Ԃ́C���������_�ɂ��Ēm�o���C�Z���Ԃ̑��ΓI�ȕω��X���i�����W���Ȃǁj����{�I�Ɏ�e���āC���̏������s���悤�Ȃ���Α��ΓI�ȑ���l����o������Ƃ��������i���_�E�ʒu�̖��j�Ƃ����Q�̖�肪�C���f���̊�{�I�Ȗ��ƌ�����D
�ΐ��R���X�|���f���X����
�ʏ�̃R���X�|���f���X���͂́A�N���X�\�̓x�������ӓx���ɂ���āA�J�C�Q�擝�v�ʂ̂悤�ɒ������āA�z�u�����߂邪�A���̍l�����́A�N���X�\�̃Z���̓x�����Q�ߓI�Ƀ|�A�\�����z�����邱�ƂƊW������B�|�A�\�����z��z�肷��x���̏ꍇ�A�ΐ��ϊ������邱�Ƃɂ��A�����S�̂ɍL���鐔�l�ɕϊ��ł��邱�Ƃ���l����ƁA�R���X�|���f���X���͂Ȃǂ̐��I�����́A�ΐ��ϊ���̐��l��p�����������R�ł���B���̍l�����́A�ΐ����`���f���ƈ�v���Ă���B�܂��A�ΐ��ϊ���̃R���X�|���f���X�s��ւ̕ϊ��́A���U���͂Ɠ����悤�ɁA�s�Ɨ�����̕��ϒl�ɂ���ĂȂ����B���������āA�R���X�|���f���X���͂̐��I�����́A�ΐ��ϊ���̐��l�̍s�C��̕��ϒl�ɂ���čs���邽�߂ɁA���U���͂̌��ݍ�p�i�J��Ԃ����Ȃ��ꍇ�̎c���j���̂͂��邱�Ƃɓ�����B���̌��ݍ�p���́A�ϐ��Ԃ̃v���t�B�[�������̕��͂ɓ�����i�`�݂̗̂ގ��x���́j�B�}�̓K�p��̂悤�ɁA�R���X�|���f���X���͂̑ΐ����f���́A�z�u�����ӂɎU��邱�Ƃ����Ȃ��A�܂Ƃ܂�悭���z����B�܂��A�x���̏������f�[�^���A�ʏ�̃R���X�|���f���X���͂ł́A�덷�Ƃ��Ē��S�ɏW�܂�X�������邪�A�ΐ����f���̏ꍇ�ɂ́A�|�A�\�����z�Ɠ��l�A�������x�����r�I�L���ɐ�������A���R�ȕz�u�����������B�u�R���X�|���f���X���̗͂��p�@�v�i2005���j2730�~�Q��.
�ΐ����`���f��
��ʂɏo���x���ł���ړI�ϐ���ΐ��ϊ������ꍇ�̗v�����̓��f���D�o���x���̑ΐ��ϊ����|�A�\�����z�̎��R�ꐔ�ɂȂ�̂ŁC�|�A�\����A���̓��f���ƌĂ�邱�Ƃ����邪�C�T�O�I�ɂ͓����ł͂Ȃ��D����l�Ƀ|�A�\�����z�����肵���ꍇ�ɂ́C�Ŗޖ@�ɂ���āC���`���f���̃p�����[�^�𐄒肷��D���͂���Y���Ґ��̊������C��Y���Ґ��̑傫���Ɉˑ����Ȃ��ꍇ�ɓK������D
�ΐ����`���f���Ƒΐ����K���f��
�ΐ����`���f���́C���肳�ꂽ�x����ΐ��ϊ������ϗʂɂ��āC�v�����̓��f���i���`�\���q�j��K�p����ꍇ�ł���C����l���|�A�\�����z������ꍇ�ɓK�p�����i�u�ΐ����`���f���v�C�u�|�A�\����A���́v�ȂǎQ�Ɓj�D�ΐ����`���f���ł́C�ΐ��ϊ����ꂽ��̕��z�ɂ��Ă̓����ɂ͌��y���Ă��Ȃ��D���������āC����덷�̓|�A�\�����z�ɂȂ�̂ŁC�p�����[�^�̐���@�́C�����Ƃ��čŖޖ@��p���邱�ƂɂȂ�D
�@�ΐ����K���f���́C�ΐ��ϊ�������̕ϗʂ����K���z����Ƃ������Ƃ��Ӗ����郂�f���ł���D�v�����͂̕��������ŕ\�킷�ƁC�ΐ����`���f�����ΐ����K���f���������悤�Ȍ`�ɂȂ�D�������C�덷���U���قȂ��Ă���̂ŁC�ΐ����K���f���́C�ΐ��ϊ���ɐ��K���z������Ƃ������肩��C�p�����[�^�̐���ɂ́C�ŏ��Q��@���p������D���ۂ̕��͂ɂ����ẮC�f�[�^���番�z�̌`���m�F���ׂ��ł��邪�C�ߋ��̕��͌��ʂ��Q�l�ɂ��āC�O�����Đ��K���z�̉�������ĕ��͂����邱�Ƃ������D�ŏ��Q��@�́C����̋Z�p�Ƃ��Ďg���邱�Ƃ��������C���K���z�����Ȃ��ꍇ�ɂ́C�K�������ǂ�����l�ɂȂ�Ȃ����Ƃ�����D
��Q��̌��i���v�I��������Q�Ɓj
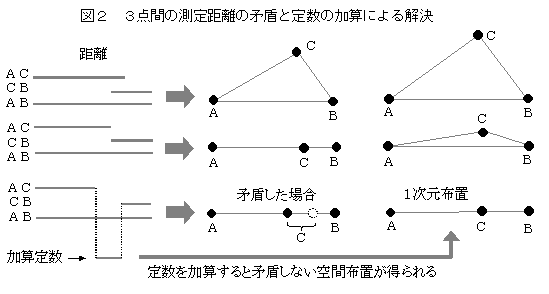
���v�I��������ł́C�N���������ۂ����R���Ɖ��肵�Ă��̊m�����v�Z���C�߂����ɋN����Ȃ��悤�Ȋm���Ȃ�C���R�ł͂Ȃ��ƍl����D���R�ɋN�������\�����Q�����Ƃ��C���R���ۂ��̔��萅�����T���i20��ɂP��̊����j���Ƃ���C�m���Q���i50��ɂP��j�̎��ۂ͋��R�ɋN�������Ƃ͍l���Ȃ����ƂɂȂ�D�����C�m����10���i10��ɂP��j�ł������Ƃ���ƁC���R�ɋN���邱�Ƃ͂��܂�Ȃ����C�N����\�����������Ȃ��D�����ŁC���_�����Ȃ����߂ɁC���R�ł͂Ȃ��i�Ӗ�������j�ƌ��_���邱�Ƃ��T���邱�Ƃɂ���D���Ȃ킿�C���S�̂��߂ɁC���R�ɋN���������ƂƋ�ʂł��Ȃ����Ƃɂ���D10��ɂP��̊m���Ȃ̂ŋ��R�ł͂Ȃ��\���������D���̎��_�ł́C���f�ł��Ȃ����Ƃł��邪�C�����C���R�ł͂Ȃ��Ƃ�����C���̌��_�͌���Ă��邱�ƂɂȂ�D���̌����Q��̌��Ƃ����D
�������W�b�g���f��multi-nominal logit model�C����q�^���W�b�g���f���C��ʉ��ɒl�iGEV�j���f���Ȃ�
���W�b�g���f���i���W�X�e�B�b�N��A���͂̃��f���j�́C�Q�l�i�Y���C��Y���j�̃f�[�^�ɓK�p����邪�C�������I���̏ꍇ�Ɉ�ʉ��������f���Ƃ��āC�������W�b�g���f��������D���ʂŕ\�킹�Ȃ��������鏤�i�̑I�����ʎ�i�C�ό��n�̑I���ȂǂɓK�p�����Dpi=EXP(mVi)/{EXP(mV1)+EXP(mV2)+���+EXP(mVk)}�@�ik�̑I�����̂���i�Ԗڂ̑I�����̊����Cm�̓p�����[�^�C�u�͗v�����͂̐��`���j�D���̎��́C�X�̑I�����̂̎����p�l�i���͓x�j�̍��v�l�ɑ���C�ʂ̌��p�l�̑傫���̊������C�I�𗦂ɂȂ邱�Ƃ��������I���̃��f���Ƃ��̑I�������I���v������A�I�ɒ��ׂ郂�f���ƌ�����D���ݕϐ��ł�����p�l�i�w���������j���m���ϓ�����ƍl����Ɓi���p�l�̑���l�Ɍ덷�������Ƃ���D�����_�����p���f���j�C�m���ϓ��Ƃ��āC���ۂ̍ő�l�̕��z�ł���K���x�����z�i��d�w�����z�j�����肷��ƁC���̎������藧�D
�@�������W�b�g���f���́C�I�����Ԃ̊֘A�����Ȃ��ꍇ�i�������鐻�i�ɓ��ɃT�u�O���[�v�Ȃǂ��z�肳��Ȃ��ꍇ�Cindependence
from irrelevant alternative,IIA)�ɗǂ����Ă͂܂邪�C�I�����̑��֊W������ꍇ�C�T�u�N���[�v�̒��ŁC���p�l�̊֘A���̃E�F�C�g��������������q�^���W�b�g���f���inested
logit model�j�Ȃǂ�����D�P���ȓ���q�`���ɂȂ�Ȃ��ꍇ�ɂ́Ccross-nested
model�Ȃǂ�����D�ɒl���z���K���x�����z�������ʓI�Ȍ`���ɂ�����ʉ��ɒl���z�igeneralized
extreme value distribution�C�f�d�u�j���f��������D�f�d�u���f���́C���̓���ȏꍇ�Ƃ��āC�������W�b�g���f���C����q�^���W�b�g���f���Ccross-nested
logit���f���Ȃǂ��܂�ł���̂ŁC�\���Ƃ��ėL���Ɏg����D(Discrete choice
model,M.Bierlaire,1997,The network GEV model,M.Bierlaire,2002,The Generalized
nested logit model,Wen&Koppelman,2000�ȂǎQ�Ɓj
�������ړx�\���@Multi-dimensional scaling
�l�c�r�Ɨ��L�D�������ړx�@�ƌ������Ƃ�����D�����̑ΏۊԂ̋����Ȃǂ̍��ق�\���s��C�Ώۂ���ԓI�ɕz�u������@�i�}�b�s���O�j�Ƃ��Ēm���Ă���C���ϗʉ�͂Ɠ��l�Ɉ����Ă���D�ړx�@�Ƃ́C��ʂɎh���Ԃ̈Ⴂ��\�����f�[�^����C�S�̂̑Ώۂ��̂Ȃ��悤�Ɏړx��Ɉʒu�Â�����@�̂��Ƃ������̂ł��邪�C�R�_�Ԃ̋��������肳��Ă���Ƃ��C�Z���Q�̋����̍��v�����������ɓ�������P�����ŕ\���ł��C������Q�����łȂ��ƕ\���Ȃ��D���v���Z���ꍇ�ɂ́C����@�ɖ�肪���邩�C���[�N���b�h�������f�������Ă͂܂�Ȃ��D���̂悤�ɂ��āC�ꎟ���̎ړx�\���@���瑽�����̎ړx�\���@�����W�������Ƃɂ��C�����f�[�^������W�l�����߂邱�Ƃ��ړx�\���Ƃ������ϗʉ�͂Ƃ͕ʂ̖��O�ɂȂ��Ă���D���ۂ̐��l��͂ł́C�������猴�_����̃x�N�g���̐Ϙa�֕ϊ����邱�Ƃ��s���āi�����O�E�n�E�X�z�E���_�[�̕ϊ��j�C�ŏ��Q����Ƃ��Ă̎����̏������ŗL�l�E�ŗL�x�N�g���ɂ���ċߎ�����̂ŁC���ϗʉ�͂Ɠ����l�ȉ�@�̂Ȃ�D�����̂悤�ȃ��g���b�N�Ȑ��l�ł͂Ȃ����Ă��邩���Ă��Ȃ����Ƃ����悤�ȏ�����l�Ԃ̍s���ɂ͓K�p�ł��邱�Ƃ��������Ƃ���C�\�����ꂽ��Ԃɏ�����Č������Ƃ��ɂ悤�ɂ���m�����g���b�N�l�c�r���������p����Ă���D�m�����g���b�N�l�c�r�́C�������̏������@�ł���P����A�@�Ɣ���`�̃p�����[�^����@����\������Ă���D
�uM-01 �l�c�r�E���ϗʉ�́v�ɂ͉��p�Ⴊ�����D�uM-02 �m�����g���b�N�l�c�r�v��Kuruscal�̃m�����g���b�N�l�c�r�̉�����D�uA-20 �l�����l�������l�c�r�v�͌l���͂��邽�߂̂l�c�r�D�uA-31 �o�n�u�v�l����ԂƎh����Ԃ�ʂɋ��߂���@�D�uA-69 �h�m�c�r�b�`�k�v�l�����g���b�N�l�c�r�̈�D�uA-70 �R�����q���́v�l����ԁC�h����ԁC�ړx��Ԃ����߂郁�g���b�N�ȕ��@�D
���d������multiple co-linearity�̖��
�d��A���͂��s���Ƃ��C�Ɨ��ϐ��ԁi�����ϐ��ԁj�̑��ւ��������Ƃ��Ӗ�����D�d��A���͂̐����ϐ��́A�{���A�݂��Ɉ��ʊW�̂Ȃ��ϐ��ƍl������ꍇ�ɗp������̂ŁA�Ή�A�W���́A�����ϐ��Ԃ̑��W�����Ȃ��Ƃ��̐���l�ɂ�����B�����ϐ��Ԃ̑��ւ����܂�ɍ����Ƃ��ɂ́A����l���s����ɂȂ�B����́A���̂����̂悤�ɍג����U������_����A���ʂ̌X���𐄒肷�邱�ƂɗႦ�邱�Ƃ��ł���B�P�P�ʂ̌덷���A�L�����ʂ̏ꍇ�i���d�������̂Ȃ��ꍇ�j�̐���ɂ͔�r�I��肪���Ȃ����A�ג����z�u�̏ꍇ�ɂ́A�덷�����_�̈ʒu�ɂ���Đ���l���傫�����ς��Ă��܂��B�����덷�ł��邪�A�����ϐ��̂Ƃ���ɂ���Đ���l�̕s���肳���قȂ邱�Ƃ������Ă���B�ł��邱�ƂȂ瑽�d�������͔�����ׂ��ł��邪�A�����ꏭ�Ȃ���A���d�������I�ȃf�[�^����舵�����Ƃ��d��A���̖͂{���̖ړI�ł���ƌ�����B���Ȃ݂ɁA�����ϐ��Ԃɑ��֊W�����邱�Ƃɂ���āA�Ή�A�W���̕����ƒP���W���̕����Ƃ��قȂ邱�Ƃ́A���d�������Ƃ͒��ڊW���Ȃ��B�{���A�����ϐ��Ԃɑ��֊W�i���ʊW�j������ꍇ�ɂ́A�Ή�A�W���ɂ́A��̓I�ȈӖ����Ȃ��̂����ʂł���B���̈Ӗ��ŁA�����ϐ��ԂɈ��ʊW��z�肵���ꍇ�ɂ́A�d��A���͂Ƃ͕ʂɏd���֖@�ƌ������Ƃ�����i�Ť1980�j�B
���d�R���X�|���f���X����
���d�N���X�\�i�R���\�Ȃǁj�̃R���X�|���f���X���́B�R���\�̕��͂ɂ́A�����̂Q���\�i�Ⴆ�ΔN��ʂȂǁj��ʁX�ɕ��͂�����@�̂ق��A�����̂Q���\���c�ɕ��ׂĂP�̂Q���\�Ƃ��ĕ��͂���ꍇ�i����v�f����ԓ��ł̕ω��E�ړ��Ƃ��đ�������j�A�R���R���X�|���f���X���͂̏ꍇ�i�R�̑��̗v�f���ԂɈʒu�t����ꍇ�j�A�O�����͂�K�p����ꍇ�i��̂Q���\�ɂ��ĕ��͂��āA���̂Q���\�̗v�f�͒lj�����ꍇ�j�Ȃǂ�����B���d�R���X�|���f���X���͂́A�R���f�[�^���Q���\�̌`�ɂ��ĕ��͂���̂ŁA���͂��ȒP�ł���A���ʂɂ��Ă��A�����v�f�̓_�������ʂɋ��߂���̂ŁA���n��I�Ȉړ��A�����ʂ̓_�̕ω��ȂǁA���߂����₷���\���`���ɂȂ�B
���d���ʕ��͖@�i���ʕ��́C���ʉ��Q�ނȂǎQ�Ɓj
���ʕ��͂́C�����̓������珊���Q��\������Ƃ��ɗp������@�ł���D�w���ҌQ�C��w���ҌQ�ȂǁD���d���ʕ��͂́C�R�ȏ�̌Q��\������Ƃ��ɗp������D�R�Q�̂Ƃ��ɂ͂Q�̓Ɨ������\���������i�Q�����j���p������D�S�Q�̂Ƃ��ɂ͂R�����i�����N���R�j�ɂȂ�D�Q��\��������@�Ƃ��āC���ʕ��͖@�┻�ʊ��@�C���ʉ��Q�ނȂǂ�����D���ʕ��͖@�͂Q�Q�̔��ʂ̂Ƃ��C���ʊ��@�͑��Q�̔��ʂ��Q�Q���Ƃɍs�����̑g�ݍ��킹�ɂ���ė\������D���ʉ��Q�ނ͌Q�̓�����\���ϐ����J�e�R���[�̂Ƃ��ɗp������D
���d��rmultiple comparison�i���U���͖@�ȂǎQ�Ɓj
���U���͂ɂ���đ����̕��ϒl�ɍ������邩�Ȃ��������肷��̂́C�f�[�^�S�̂ɂ��āC�v���Q�̕��ϒl�������Ƃ��̕��U�ƕ��ϒl���l�������Ƃ��̕��U�̑召��r������D���������āC����̕��ϒl�ɒ��ڂ��Ȃ��ŁC���U�̑召�Ŕ��肷��D�X�̕��ϒl�ɒ��ڂ��āC�ǂ̕��ϒl�Ƃǂ̕��ϒl�ɍ�������̂��ׂ邱�Ƃ́C���ϒl�̑��d��r�̖��ƌ�����D���ϒl�̐��������Ƃ��ɂ́C�Q�̕��ϒl�̑g�ݍ��킹���l����ƁC���̑g�ݍ��킹�̐��������̂ŁC�{���C���ϒl�ɍ����Ȃ��Ă����R�ɍ��̏o��\���������Ȃ�Dt������Q��ƁC�P���ɍl����ƁC���R�ɗL�ӂɂȂ�m�����Q�{�ɂ��Ă���i�������Q������Ɠ�����m�����Q�{�ɂȂ�̂Ɠ����C���ۂɂ͂Q�̂�����͓Ɨ��ł͂Ȃ��̂łQ�{�ɂ͂Ȃ�Ȃ��j�D���������āC�S�̂̌���ŗL�ӂɂȂ�����C���d��r������ɂ́C���炩�̌`�ŋ��R�̊m������������K�v������D���d��r�̕��@�ɂ́C�������̕��@���l�����Ă���D
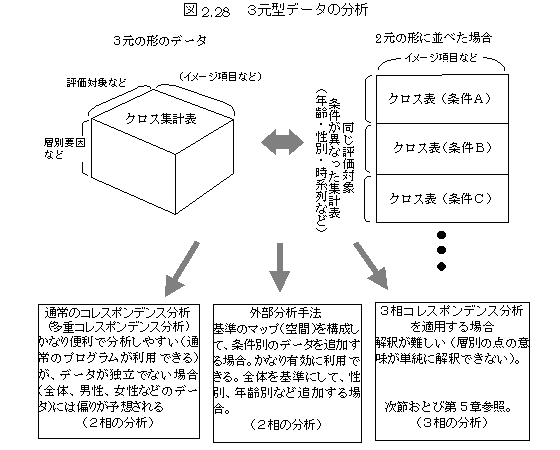
�����O���R���X�|���f���X����multi-mode external correspondence analysis���O�������R���X�|���f���X���́i���̒lj��j
���ϗʉ�A���͂̈�ʓI�Ȏd�g��
�@�ړI�ϐ��A�����ϐ����Ƃ��ɕ����̏ꍇ�̉�A���͂͑��ϗʉ�A���͂ƌ�����B�����Ƃ��ẮA���ϗʊԂ̊֘A���͂��镔���Ɨv�����ʂ����肷�镔�������ϗʉ�A���͂ł���A���ϗʊԂ̊֘A���s��i���ϗʕW���Ή�A�W���s��j�̎听�����͂��������͂ƌ����A�Q�̕���������B�������֕��́A���ʉ��Q�ށA���d���ʕ��͂Ȃǂ́A��҂̑��ϗʊԂ̊֘A���s��͂�����@�ł��邪��v�Z�̏o�͂ɂ͑��ϗʉ�A���͂̐������i��ʉ�����W���⑊�֔�Ȃǁj�Ȃǂ̎w�W���܂܂�Ă��邱�Ƃ���A���ϗʉ�A���͂̕������ӎ�����Ȃ����Ƃ������B���ϗʕ��U���͂́A���ϗʉ�A���͂̌��蕔���ɂ����邪�A���ϗʉ�A���͂̕��U�̕���������̂Ƃ��̈�ʉ����U�Ɛ��`�W�ɂȂ��̂ŁA���ϗʕ��U���͂́A���ϗʉ�A���͂Ƃ͕ʂ̕��@�ƌ�����B���ϗʕ��U���͂́A���U�s��̕����Ƃ��̍s����v�Z�ł���ق��A���U�s��̌ŗL�l������͂̌ŗL�l������v�Z�ł���̂ŁA���ϗʉ�A���͂̌��ʂ���ȒP�Ɍv�Z�ł���
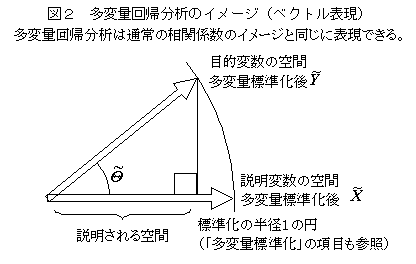
���ϗʉ�A���́i�R�ϐ��Q�̏ꍇ�j
�@�ϐ��Q��1�̋�ԃx�N�g���Ƃ��ĕ\������ƁA�d��A���͂̃x�N�g���C���[�W�Ɠ����悤�ɁA�R�̕ϐ��Q�̊W�́A�}�̂悤�ɕ\���ł���B���������āA���ϐ��Q�Ԃ̉�A���͂́A�����ϐ��Q�Ԃ̕ϐ����������������ϐ���Ԃɑ���]���ϐ��Q�̎ˉe�ɂ�����̂ŁA�����ϐ��Q���Q�̋�ԃx�N�g���ɕ������A�����ϐ���Ԃɒ��������ԃx�N�g���̓Ǝ����U�i���ϗʕW������̓��ύs��̂Q��a�j���덷�ɂȂ�A�����ϐ���ԂɊ܂܂��ϐ��Q�̑��ϗʕW������̓��ύs��̂Q��a���A����W���̕��U�ɂȂ�B���̌���W���s��́A�R���̌`�ɂȂ邪�A�v�f���݂��ɓƗ����Ă���̂ŁA�Q���̌`�ɕ��בւ��Ă��\��Ȃ��B�R�̌Q�̐������֕��͂����ϗʉ�A���͂Ɠ����`���ɂȂ邪�A�֘A���̍s��i�R���̌`�j�̈��q�����߂�Ƃ��ɂ́A�R���听�����́i�R���听�����́j��p����B�܂��A���̈��q�́A�Q���f�[�^�̌`�ɕ��������Ƃ��̈��q��p���邱�Ƃ��ł���B
���ϗʉ�A���͂̐������w�W�i�������֕��́A�d���ʕ��́A���ʉ��Q�ށA���ϗʕ��U���͂Ȃǁj
�@�ړI�ϐ��������̏ꍇ�̗v�����͂ł��鐳�����֕��́A�d���ʕ��́i�������ʕ��́j�A���ϗʕ��U���́A���ʉ��Q�ނȂǁi��ʓI�ɑ��ϗʉ�A���́j�́A��{�I�ɓ����v�Z�@�ɂȂ�̂ŁA�������̎w�W�͋��ʂ��Ă���B�傫�������āA���ϗʂ̕��U�i��ʉ����U�⃩���v�ʂȂǁj�W�̎w�W�ƖړI�ϗʂ̌ʂ̕��U�𗘗p�����w�W�ɕ����邱�Ƃ��ł���B
�@��ʉ����U�͑��ϗʂ��璼�ڒ�`����A�v�����ʂ̓����v�ʁi�덷�����j��x�N�g�����ցi�����������j�ŕ\����A�L�Ӑ�����ɗp������B��ʉ�����W���́A�ʂ̕��U���瑊�֕������������ꍇ�̗v�����ʂ̎w�W�ł���A�璷���W���́A�ʂ̕��U�̍��v�i���֕����������Ȃ����U�j�ɂ��Ă̐������w�W�ł���B���֔�A�������W���Ȃǂ́A��ʉ�����W���n���̎w�W�ł���i�u���ϗʉ�A���́E�������֕��́E���ϗʕ��U���́v(2006�N��)�Q�Ɓj�B

���ϗʉ�͂̒�`
�@���ϗʉ�͂́A�K���I�ɂ́A�����̂悤�ɂ܂Ƃ߂��邪�A�{���ł́A���̂悤�ɒ�`���Ă���B
�@�����̕ϐ�����舵���ꍇ�A�ʏ�̑���f�[�^�ł́A���݂̑��֊W������̂ŁA���ʊW�Ȃǂ͂���ꍇ�ɑ��ւ��镔���𑽏d�Ɏg��Ȃ��悤�ɂ���K�v������B���ւ��镔������菜�����@�́A�Ɨ�������p����Ƃ��ɂ͎听�����͂ł���A�����ł͂Ȃ����ɕϐ���p����ꍇ�ɂ́A��q�́u���ϗʕW�����v�ł���B���������āA���ϗʂ�p���ĕ��͂���ꍇ�ł��A���ւ��镔���𑽏d�Ɏg��Ȃ��悤�Ȍ`�ɂ��ĕ��͂�����@�����ϗʉ�͂Ƃ������Ƃ��ł���B
�@�听�����͂���q���͂́A�Ɨ��������̂��̂����߂�悤�ȑ��ϗʉ�͂ł���A�d��A���͂́A�����ϐ����ɂ��đ��ϗʕW�������s���Ă���̂ŁA���ϗʉ�͂ƌ�����B���ϗʉ�A���́A�������֕��́A���ʉ��Q�ށA���d���ʕ��͂Ȃǂ́A�����ϐ��ƖړI�ϐ��̗����ɂ��đ��ϗʈ����i���֕����𑽏d�Ɏg��Ȃ����Ɓj�����Ă��鑽�ϗʉ�͂ł���B���ϗʕ��U���͂́A�ϐ��x�N�g���i���U�j���瑊�֕����������Ƃ����悤�ȏ�L�̑��ϗʉ�͂Ƃ͈قȂ�A�u��ʉ����U�v�Ƃ������֕�����p���Ȃ��Ǝ��̕��U���`���Ă��鑽�ϗʉ�͂ł��邪�A��{�I�ɂ͑��֕����𑽏d�Ɏg��Ȃ��悤�ȑ��������z�i�E�B�V���[�g���z�j��p���ăJ�C�Q�����ʉ������ꍇ�ɓ�����B���̂ق��A�}�n���m�r�X�̋����́A���ϗʂ̑��֕����̑��d������������̃��[�N���b�g�����ł���A�t�B�b�V���[�̏��ʂ͑��ϗʈ����������ꍇ�́i���֕����̑��d������������́j���ϗʂ̕��U�Ƃ������Ƃ��ł���B�������u���ϗʉ�A���́E�������֕��́E���ϗʕ��U���́v(2006)�A�u�f�[�^���͓���Q�@���ϗʉ�͖@�E�l�c�r�̉��p�v(2008)�ȂǎQ�ƁB
���ϗʉ�͖@multi-variate analysis
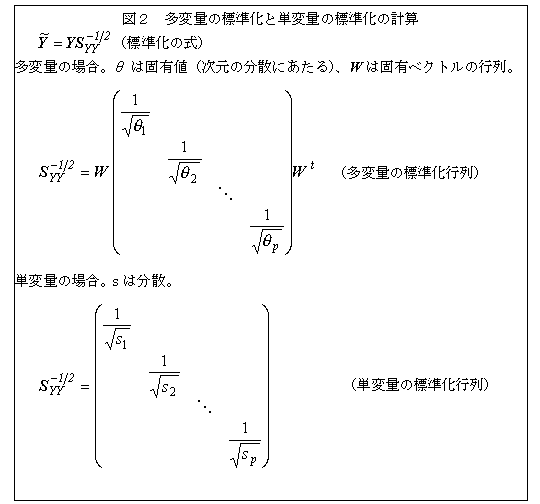
���ϗʂ͂�����@�̑��́D���q���͖@�C�d��A���͖@�C���ʕ��͖@�C���ʉ��T�C�U�C�V�C�W�C�������֕��͖@�C�N���X�^�[���͖@�Ȃǂ���\�I���@�D��@�́C��ϐ��ɑ��鑊�ւ̍ő剻�i���U�̍ő剻�j�C�c�����U�̍ŏ����Ȃǂ̊�ʼn����̂ŁC�قƂ�ǂ̉�͖@�������悤�ȕ��@�ɋA������D�����Ӗ��ł́C�ړI�ϗʂ����ϗʂ̏ꍇ�i���ϗʐ��K���z�Ȃǂ̑��ϗʕ��z��z�肷��ꍇ�j�������C�d��A���͂Ȃǂ͂P�ϗʂł��邪�C��ʓI�ɁA���ϐ����������͖@�𑽕ϗʉ�͂ƌ����Ă���D

���ϗʉ�͂ɂ����鎿�I�i�����́j�Ⴂ�ƗʓI�i���_�́j�Ⴂ
���q���̗͂�Ō����Ȃ��,���q���邢�͈��q��Ԃ̈Ⴂ�����I�Ⴂ�ƌ����C���q���_�̍��ق�ʓI�Ⴂ�ƌ�����D���q���_�͌l���̖��ł���C���q��Ԃ́C���ׂĂ̌l�i�T���v���j�ɋ��ʂ��Ă���D�l������ɂ���Ƃ��ɂ́C���q��Ԃ����ɂ��āC���_�̑召�̈Ⴂ�ɂ���ĕ\������D���������āC���ʈ��q��Ԃ��ɂ��Ȃ���C�l���̔�r�͂ł��Ȃ��̂����ʂł���D���ʈ��q��Ԃ́C����C�ړx�i���̂����j�ɂ�����D���ϗʉ�͂𗘗p����Ƃ��ɂ́C�����̍��فi�ړx�̍��فj�����邱�Ƃ����C�ړx�ő���ꂽ���_�̍��ق��������Ƃ����v���������D��ʂɁC���ϗʉ�͂ł́C�����C���q�C��Ԃ̖��i�ړx���邢�͎��I�Ȗ��j�ƁC���̎ړx�ő���ꂽ���_�̑召�̖��i�ʓI�Ȗ��j�̂Q�̗v�f���܂�ł���D���������āC�����I�ɂ́C�Q�̗v�f�����邱�Ƃ��ł���D���p�I�ɉ��l�̍������@�́C���I�ȋ�ԁi�ړx�j��T�d�ɒ�߂Ă����āC���_�݂̂𑪒肵�Ĕ�r���邱�Ƃł���D���n���r������ʂ̔�r���L���ɍs����D�����ł́C���̂悤�ȕ��@���C�O�����͂Ƒ��̂��Ă���D�v�����ʂ���舵���ꍇ�C����̊��̍��قƗv���̍��ق́C��{�I�ɕ����ł��Ȃ��̂ŁC�l������O���v���́C�ړI�ϐ��Ɠ����ɕK�����肵�Ă����āC���������i���������j���C�����ł��������ǂ����m�F�ł���悤�ɓw�͂���K�v������D�i�O�����͂̍��Q�Ɓj
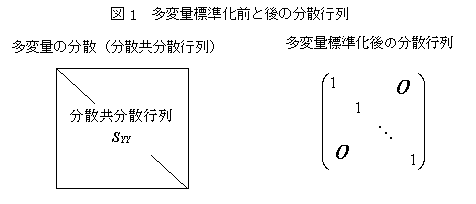
���ϗʕW����
�@���ϗʃf�[�^�́A�ϐ��Ԃɑ��֊W������̂ŁA�S�̂Ƃ��Ă܂Ƃ߂āi�P�̋�ԂƂ��āj���̕ϐ��Ƃ̊֘A���i�v�����ʂȂǁj������ꍇ�A�@���ւ��镔���𑽏d�Ɏ�舵��Ȃ����ƁA�A���ϗʂȂ̂Ŋe�ϐ��̒P�ʂ�W���I�ɂ��邱�Ɓi�g���Ƒ̏d���Ɏ�舵���Ƃ��Ȃǁj�A�̂Q�̑��삪�K�v�ł���B�P�ϗʂ̏ꍇ�ɂ́A�W�����Ŋ��邱�Ƃɂ���ĕW�����_���v�Z����B
�@���ϗʂ̏ꍇ�ɂ́A���֍s��i���U�����U�s��j�̋t�s��̕������s���p����B���̈Ӗ��́A�@���ϗʂ𐬕��ɕ�������i�ŗL�l�A�ŗL�x�N�g�������߂�ƌŗL�l�ɕ��U�����f����j�A�A���𐬕��̕��U���P�ɂ���i�ŗL�l�̕������Ŋ���j�A�B���Ƃ̕ϐ��̕����ɕ�������C�Ƃ������ƂɂȂ�B
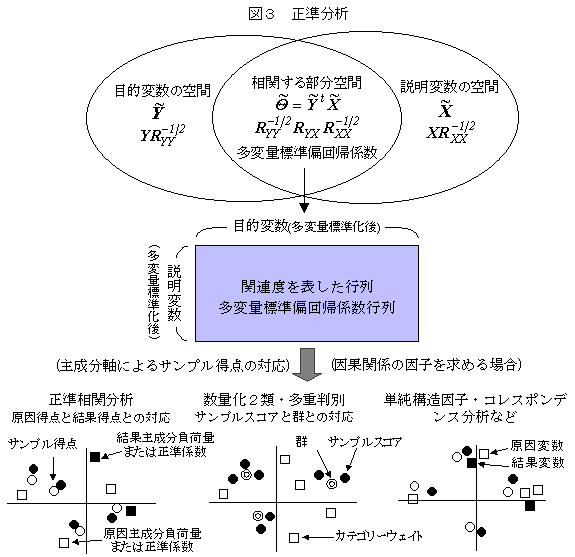
�@���̂��Ƃɂ���āA�}�P�̂悤�ȕϊ����Ȃ���A���ϗʂ̕��͂��s����i���ϗʉ�A���́E�������֕��́E���ʉ��Q�ށE�d��A���͂̐����ϐ��Ȃǁj
���ϗʂ̕��U���́i�l�`�m�n�u�`�j�E���ϗʉ�A����
�@����l����������ꍇ�A����l�i�ړI�ϐ��j�̕��U�͕��U�����U�s��i���U�s��Ɨ����j�ŕ\�������B�v�����ʂ̌���́A�ړI�ϐ��̕��U�s���v���ɂ���ĕ���������U�s��̕��U�w�W�ł����ʉ����U��p����B
�@����l�Ԃɑ��ւ�����ꍇ�ɂ́C�X�̕ϐ���ʁX�Ɍ��肷��ƕ��U�𑽏d�Ɏg�����ƂɂȂ�̂ŁA���̂悤�Ȃ��Ƃ̂Ȃ��悤�ɁA���ϗʂ��Ɏ�舵����ʉ����U��p����B����ɂ́A�ϗʂ̑��ϗʐ��K���z�A���U�s��̃E�B�V���[�g���z�i�J�C�Q�敪�z�̑��ϗʂւ̊g���j��z�肷�邱�Ƃɂ���Ē�`�����ޓx�䓝�v�ʃ����g����B
�@���́A���U�s��̍s����v�Z����邪�A���ϗʉ�A���͂�����֕��́A���ʉ��Q�ށA���d���ʕ��͂̏ꍇ�A�s��p���Ȃ��ŁA�����听���̌ŗL�l���璼�ڌv�Z���邱�Ƃ��ł���B
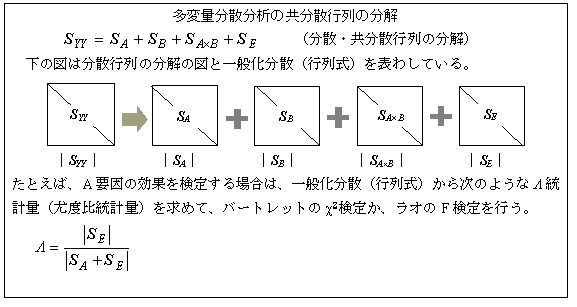

�_�~�[�R�[�f�B���Odummy coding�i�O�P�^�R�[�f�B���O�j
�@�J�e�S���[�ϐ��ɂ��Đ��ʓI�ȕ��͂�����Ƃ��ɁC�J�e�S���[��01�ϐ��Ƃ��ĕ\������D�J�e�S���[�ϐ��́A�J�e�S���[���}�C�i�X�P��01�ϐ��ɕϊ�����A�d��A���͂Ȃǂ̐��ʓI���͂�K�p���邱�Ƃ��ł���B�}�̂悤�ɁA�Ō�̃J�e�S���[�ɂ��ׂĂO��^���A���̃J�e�S���[�́A�Y������J�e�S���[�ɂP��^����B
�@�v�����͂̐����ϐ��Ɏg�p����ꍇ�A�R�̃J�e�S���[�͂Q�������ʂ��`������i�����N���Q�j�B�قȂ����R�_�����ʂ��`������̂Ɠ����B�v�����͂̏ꍇ�A���ʂɑ���ړI�ϐ��̎ˉe�����ƂȂ�̂ŁA�ǂ̂悤�ȓ_���Ƃ��ĕ��ʂ��`�����Ă��\��Ȃ��B���������āA�R�̃J�e�S���[�ɗ^���鐔�l�͖����ɂȂ�B���̒��ŁA�Ō�̃J�e�S���[����_�ɂ��āA���̃J�e�S���[�ɑ��č��W����̂P�̈ʒu��^����A��A�W�����A���̃J�e�S���[�Ƃ͖��W�ɁA��J�e�S���[�Ƃ̍��Ƃ��ĕ\�������̂ŁA�J�e�S���[�̌��ʂ�����Ƃ��ɓs�����ǂ��B���̃R�[�f�B���O�@���_�~�[�R�[�f�B���O�ł���A���U���́A���ʉ����͂ȂǁA�ł������g����B�v�Z���ꂽ��A�W������A�Ґ����l�����ĕW�����_�i���ςO�A���U�P�j�̂��߂̃J�e�S���[�E�F�C�g���v�Z���邱�Ƃ��s����B�u�J�e�S���[�E�F�C�g�̌v�Z�v���ڎQ�ƁB
�@��L�̂悤�ɃR�[�f�B���O�@�͖����ɑ��݂��邪�A���p��A�s���̂悢�R�[�f�B���O�@�Ƃ��āA���̂ق����ʃR�[�f�B���O�A�����R�[�f�B���O�Ȃǂ�����B�ڂ������e�́C�uA-55�d��A���̗͂��p�@�v(2004��)�Q�ƁD
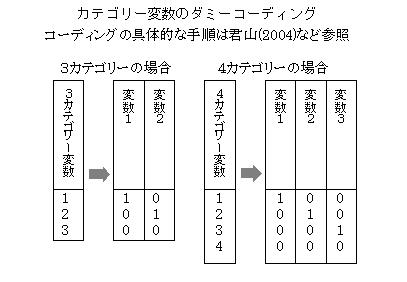
�^�����g�C���[�W�]������
���Ђł́C��ʓI�ȃC���[�W�]�����ڂɂ���ĕ]�����s���Ă���D�uJ-17�C���[�W�̑���@�v�Q�ƁD
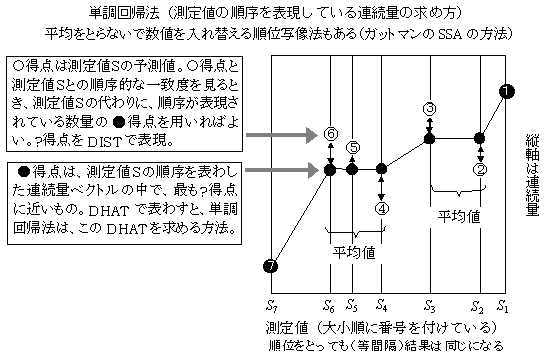
�P����A�@monotone regression analysis
����l�̏������݂̂��g����A���͂Ƃ���Kruskal(1964)�ɂ���Ē�Ă��ꂽ���@�D���Ƃ��ƁC�m�����g���b�N�i�����f�[�^�j�̑������ړx�\���@�Ƃ��čl����ꂽ���C�������̏����@�Ƃ��čL�����p���邱�Ƃ��ł���D�v�Z���@�́C���f���̍œK���̎菇�Ə������̏����ł���P����A�菇�����݂ɌJ��Ԃ��D�œK���v�Z�́C���f���ɂ���čŏ��Q��@�C�Ŗޖ@�C�K���x�w�W�̍ő剻�ȂǂɂȂ�D�P����A�菇�́C�P���W����������Ȃ��Ώۂ́C���ϒl�����߂邱�Ƃɂ���ē����ʂ�����āC�P���W�����悤�ɂ���D�S�̖̂ړI�ϐ��́C�����̑���l�ł���C���f�����������ϐ��ɂ����邪�C�v�Z��́C��������l�������ϐ��ɂȂ��āC�A���ϗʂƂ��ĖړI�ϐ����\�����邱�ƂɂȂ��Ă���D
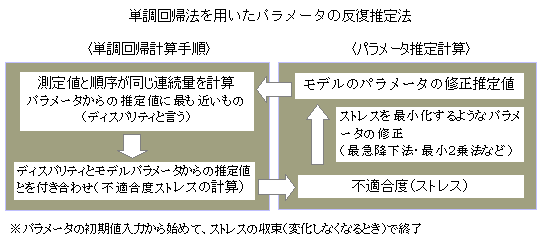
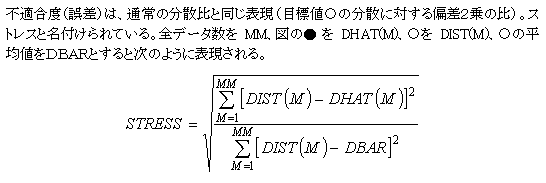
�P����A�@monotone regression analysis�̃A���S���Y��
�v�Z�ړI�̐��l���v��������u�œK�l�v�Z�菇�v�ɂ���Đ��肳�ꂽ��i�P����A�@�̍��Q�Ɓj�C�ړI�ϐ��̏����l�ɏƂ炵���킹�āC�덷���v�Z����D���������͉�͓I�ł͂Ȃ��C�A���S���Y���Ƃ��Ď�����Ă���iKruskal�C1964)�D�œK�l�v�Z�Ə����l���v���b�g���āC�����W�ɖ���������Ƃ��ɂ́C�����̂��镔���ς����l�������f�[�^�̑���Ƃ��ėp����D���̂悤�ɂ��Čv�Z���ꂽ�l�́i�}�̍��ہj�C�����f�[�^�ƒP���W�ɂ���̂ŁC�����ʂ�F�߂��`�ŁC�����l�̑���ɂȂ�A���ʖړI�ϐ��ƌ�����D���̐��l�ƁC�u�œK�l�v�Z���l�v�Ƃ̃M���b�v���덷�ƌ�����D���̌v�Z�X�e�b�v�ł́C���̐��l���]���ϐ��ƂȂ��āC�u�œK�l�v�Z�v���s����D�����������āC��������܂ŌJ��Ԃ��D�œK�l�v�Z���C�ŏ��Q��@�Ȃǂ̎��ɂ͐���̔����Ŏ������邪�C�ŋ}�~���@�̂悤�Ȑ��l�I�v�Z�@�ł́C�������x���C�ɏ��l�ɗ������ނ��Ƃ������C���O�Ɏ��ʐ����`�F�b�N�ł��Ȃ����Ƃ����ʂȂ̂ŁC����l���ׂāC�O���œK�ɂ���悤�ȑމ����������o�����Ƃ������D
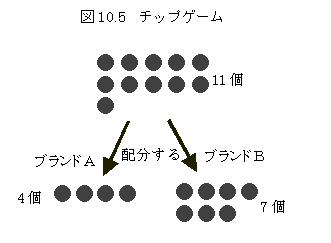
�`�b�v�Q�[���i�P��a�@�Q�Ɓj
���Ƃ��Q�̑Ώۂɂ���11�̃`�b�v���D���ȓx���ɂ���ĕ�����C�Ƃ����悤�Ȏ葱���ɂ���Ěn�D�x�𑪒肷����@�D���v�I�ɂ͍��v�l�����ɂ��ē��_��z������P��a�@�iconstant sum method�j�ƌĂ�Ă���D���̕��@���C������₷���`�ŋ�̓I�Ȏ葱���ɂ����̂��`�b�v�Q�[���ɂȂ�D
���Õs���Y�����]�����@
�uJ-28�s���Y�������i�v�Z�v�́C1980�N��̕������g���Ă���̂ŁC�p�����[�^���̂͂قƂ�ǎg���Ȃ��D�v�Z�̕��@�́C���ʃf�[�^�i���ʐρC�s�S����̎��ԋ����Ȃǁj�́C���`�������藧�͈͂�����ĒP���v�Z�i�܂���ߎ��j���C�J�e�S���[���ځi�}���V�����̕����̌����Ȃǁj�͂O�P�f�[�^�̃E�F�C�g�i�P���j���v�Z���ĉ��Z��������D�P���͋��z���̂��̂�p���Ă���D���`����ۂ��߁C�p�����[�^����̂��߂̕����́C�f�[�^�̕����\�Ȕ͈͂ōו������āC�ʁX�̕��������쐬���Ă���D�R���s���[�^�v���O�����́C�ꏊ�̎w��ɂ���āC�قȂ������������Ăяo���`���ɂȂ��Ă���D
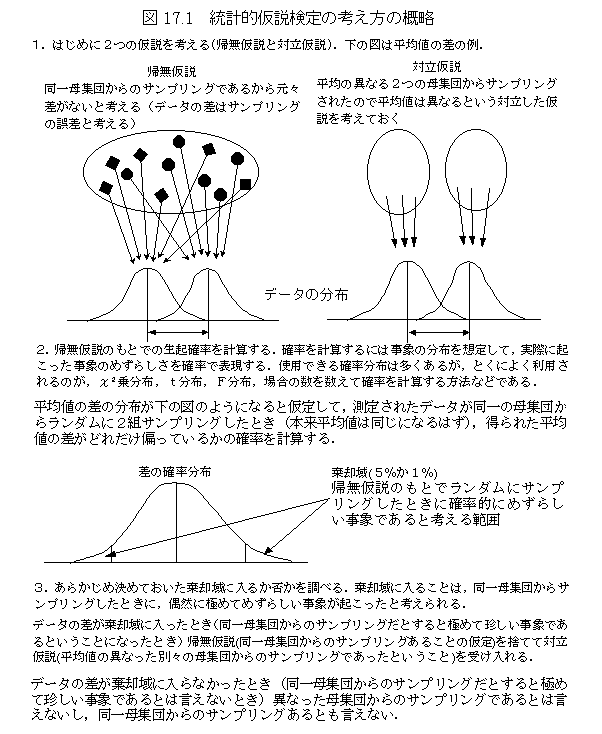
���ڊm���@�i���v�I��������Q�Ɓj
�t�B�b�V���[�̒��ڊm���v�Z�@�D���R�ɋN�������m�����v�Z����Ƃ��ɁC�A�����z��p�����ɁC�ꍇ�̐��𐔂��Čv�Z����D�x����v�����������Ƃ��ɂ̓J�C�Q�敪�z�ߎ����悭�Ȃ��̂ŁC���m�Ȋm�����v�Z���������悢�D�Ɨ��ɕω�����ϗʂ������Ȃ�ƌv�Z���ł��Ȃ��Ȃ�̂Ń�2���z�Ȃǂ𗘗p����D��ʓI�ɂ͒����z�̊m���v�Z�ɂȂ�D����ꂽ�����\���A�������ɏ]���čł������P�[�X����ǂ̂��炢�̈ʒu�ɂ��邩���v�Z���ėL�Ӑ����Ɣ�r����D�uM-31
���ڊm���v�Z�@�ƃ�2�ߎ��v�C�t�B�b�V���[�̒��ڊm���@�ƃ�2����i�J�C�Q�挟��j�̗������s���v���O�����D�uA-64
�N���X�W�v�\�̌����ƃ�2����v����̓N���X�\�̌���̕����ɂ���D
�����z
��̒��̐ԋʂƔ��ʂ����o���Ă��Ƃɖ߂��Ď��s���J��Ԃ��ꍇ�i�x���k�[�C���s�j�̊m���́C�Q�����z�̊m���ɂȂ邪�C�߂��Ȃ��Ŏ��s���J��Ԃ��ƒ����z�̊m���ɂȂ�D�����z�̏ꍇ�͂�����ɂm�����Ɏ��o���ꍇ�Ɠ����ł���D��̋ʂ̗Ⴉ�番����悤�ɁC�Q���m���́C�ʂ̏o���m���i�ʂ̊����j�����s�|�����킹�邱�ƂƁC�ǂ̋ʂ��I��邩�̑g�ݍ��킹�̏ꍇ���|�����킹�邱�Ƃɂ���Čv�Z����C���m���̏ꍇ�́C�S�̂���m��I�ԑg�ݍ��킹�Ɛԋʂł���g�ݍ��킹�Ȃǂ���v�Z�����D�ʂ̐��������Ď��o���������Ȃ��ꍇ�ɂ́C�߂��Ă��߂��Ȃ��Ă��قƂ�Ǎ����Ȃ��̂łQ���m���ƒ��m���͋߂��Ȃ�D���v�I��������ł́C�����\�̎��ӓx�����Œ肵���Ƃ��̃Z���̓x���̎�肤��ꍇ�̐��͒����z�Ƃ��Čv�Z�ł��C�L�Ӑ��̌���́C����ꂽ�����\���C�A�������ɏ]������̒��x�i�����z�̂�������̃p�[�Z���^�C���j��L�Ӑ����Ɣ�r����D
���a�@�ɂ������v��
�R���W���C���g����⊯�\���������Ȃǂɂ����āC�v���������ꍇ�ɂ́C���ׂĂ̗v�����l�������������ł��Ȃ����Ƃ�����D���̏ꍇ�C���ݍ�p�Ȃǂ��l�����ėv�����Q�Q�C�R�Q�ɕ����ĕʁX�ɒ���v���������s���D�\���̂��߂̐���l�����ʂɂ��邽�߂ɁC�e�v���Q�ɂ́C���ʂ����v�������Ă����āC����l���ŏI�I�ɒ�������K�v������D�ɒ[�ȏꍇ�͂Q�v���܂��͂R�v�������ɊҌ����邱�Ƃ��ł��邪�C�S�������̏ꍇ�ɂ́C���������̋ψꉻ�i���̏��������ɂ��邱�Ɓj������̂ŁC�ł���Ȃ�Α����̗v�������������������s���������悢�D�t�ɁC�����̗v�����܂߂Ă��C�]���ɂ͐��`�I�Ȍ��ʂ����҂ł��Ȃ��\��������̂ŁC�������e�ɂ���Ĕ��f���Ȃ���Ȃ�Ȃ��D
�����R�[�f�B���Oorthogonal coding
�J�e�S���[�ϐ��𐔗ʓI�ȕ��͂�����Ƃ��ɁC�ϐ��Ƃ��ĕ\��������@�́C�O�P�^�̃_�~�[�R�[�f�B���O�C���ʃR�[�f�B���O�C�����R�[�f�B���O�Ȃǂ�����D�R�̃J�e�S���[�̏ꍇ�C�Q�̕ϐ��Ƃ��ĕ\���ł���i�����N���Q�j���C�J�e�S���[�̈Ӗ����d������i�P�C�O�j�C�i�O�C�P�j�C�i�O�C�O�j�Ƃ����\���@�̃_�~�[�R�[�f�B���O���ł��������p����C���ʉ��P�ށC���U���͂̕\���ɗp������D�_�~�[�R�[�f�B���O�̓J�e�S���[�̃E�F�C�g�͂��̂܂ܕ\���ł���̂ŕ֗��ł��邪�C�ϐ��Ԃɑ��ւ�����̂ŁC���ݍ�p����舵���悤�ȕϊ��ɂ͕s�����ł���D���ݍ�p��\������ɂ́i�O�C�O�j�̗v�f���i�|�P�C�|�P�j���g�p������ʃR�[�f�B���O���֗��ł���D�����R�[�f�B���O�́C�ϐ��Ԃɑ��ւ��Ȃ��悤�ɃR�[�f�B���O������@�ŁC�R�J�e�S���[�̏ꍇ�C�P�̃J�e�S���[�Ƒ��̂Q�̃J�e�S���[����ʂ���ϐ��ƁC��ڂŋ�ʂł��Ȃ������Q�̃J�e�S���[����ʂ���ϐ��̂Q�̕ϐ��łR�̎��ʂ��ł���悤�ɂ�����@�ł���D�_�~�[�R�[�f�B���O�ł́C�ϐ����J�e�S���[��\�����Ă���̂������āC�����R�[�f�B���O�͕ϐ�����������Q�Q�̍��ق�\�����Ă���i���`�Δ�j�D���U���͂̑��d��r�ɗ��p���邱�Ƃ��ł���D�����R�[�f�B���O�ɗp�����鐔�l�́C���ς��O�ɂȂ�悤�ɂP�ȊO�̐��l���p�����Ă���D�w���}�[�g�̒����s���p����Ǝ����I�ȕ��͎葱���ɂ͕֗��ł���D�R�J�e�S���[�Q�ϐ��́C��{�I�ɕ��ʂ��`������̂ŁC���U���͂�d��A���́C���ʕ��́C���̑��C����������ɂ���Ƃ��ɂ́C���ꕽ�ʂ��`������Q�̃x�N�g���͓������ʂ����D���������āC�R�[�f�B���O�̕��@�͖����ɒ�`�ł�����̒�����̂ŁC�����Ƃ��s���̗ǂ��\���@��p����悢���ƂɂȂ�D�ڂ������e�́C�uA-55�d��A���̗͂��p�@�v�ߊ�5000�~�Q�ƁD
����\
�R���W���C���g����⊯�\���������Ȃǂɂ����āC�قƂ�ǂ̌��ݍ�p���Ȃ��Ƃ���Ƒ�������Ȃ����Ď������s�����Ƃ��ł���D�v�����������Ă���Ƃ������Ƃ́C��̗v���̐����i���\�����̕]�����������i��R���W���C���g����̐ݒ肵�����i�����Ȃǁj�ɑ��̗v�����ψ�ɍ�p���Ă��邱�Ƃ��Ӗ����Ă���̂ŁC���ϒl�̍�����邱�Ƃɂ���đ��̗v�����ʂ��������Ƃ��ł��C�����Ԕ�r���ȒP�ɂł���D�����̗v���ɂ��āC�ǂ̗v�����Ƃ��Ă��C���̗v���̐����ɑ��āC���̗v���̐����������������g�ݍ��킳�ꂽ�ꍇ�̂����C�ł��������ꍇ��\�̌`�ɕ\�����̂�����\�ł���D�v���̐������������Ă���ꍇ�ɂ́C���Ȃ����̑���ł�����v�����������邪�C�������s�K���I�ł�������C���������肷��Ƒ���������Ă��܂��D��������Ȃ�����ɂ́C����\�ɋ^�������̊���t���C�v����g�ݍ��킹�C���a�^�����C�w����\�̗��p�Ȃǂ����邪�C�v�����������Ȃ��ꍇ�ɂ́C���͖@�ɂ���ėv�����ʂ̌��z�𐄒肷��K�v������D
�����@method of adjustment, Herstellungsmetode
���邳�Ⓑ���ȂǁC�]���Ώہi�W���h���Ƃ����j�ƐS���I�ɓ�����������傫�����C�������u�����邱�Ƃɂ���đ��肷��D��ʂɁC���͂̏��ω�����ƁC�P���Ȓ����ł����Ă��C�����������钷���͔����ɈقȂ��Ċ�������̂����ʂł���i�����}�`�Ȃǁj�C���̗ʂ𑪒肷��Ƃ��Ȃǂɗp������D�P��@�C�Ɍ��@�i�ɏ��ω��@�j�ȂǂƂƂ��ɁC�S����������@�̊�{�I�ȑ���@�̈�ŁC����̘c�݂��N����Ȃ��悤�Ɏ葱�����m������Ă���D�l�Ԃ̒m�o�@�\���������邱�Ƃɗ��p����C���p�I�ɂ́C�قƂ�Ǘ��p����Ă��Ȃ��D
�荇���^�s�����u���b�N�v��i BIBD�jbalanced incomplete block design
�����̖ړI�ɂȂ��Ă��鑪���̏������ōs�����Ƃ�����Ƃ��ɂ́C�������u���b�N�����āC�u���b�N���ň�ʂ�̑�����s���ꍇ�𗐉�@�Ƃ����D���\�����̏ꍇ�̂悤�Ɏh���̐��������Ȃ�����C�h���̊Ǘ�������Ȃ�ƁC����@�����i�����^�����j���ł��Ȃ��D���̂悤�ȏꍇ�C�����̖ړI�ł͂Ȃ������̐���v���ł���u���b�N�̉e�����C�ړI�̗v���ɋψ�ɍ�p����悤�ɓw�͂���D�Q�̎h���������u���b�N�Ŏ�������邱�Ƃ���Ƃ������C���ׂĂ̎h���ɂ��ĉ�������ɂȂ�ƃu���b�N�v�����ψꉻ���Ă���ƍl�����C�ނ荇���Ă���Ƃ����D���̂悤�Ȍv���ލ��^�s�����u���b�N�v��Ƃ����D�u���b�N�v��͔_��ł̕i��Ȃǂ̗v�����ʂ��m���߂邽�߂ɍl���o���ꂽ���C���\�����Ȃǂ̐S�������ł��悭���p�����D�]���҂�������̃u���b�N�ƍl���āC�Q������^�u���b�N�v��𗧂Ă邱�Ƃ����邪�C�]���҂̐l�������C�a�C�Ȃǂ̔����C�܂��u���b�N�������܂葽���ł��Ȃ��Ȃǂ̐���̂��߂ɁC�u���b�N�v���i������Ȃǁj���ψ�ɂȂ�悤�ɁC�ł��邾���ނ荇���悤�ɍH�v�����v��𗧂Ă���Ȃ����Ƃ������i�ꕔ�ލ��^�s�����u���b�N�v��j�D
�e�B�[���Y�̉��l��
1990�N��O���ɍs��ꂽ��������e�B�[���Y�̃^�C�v��������������D�uJ-05�e�B�[���Y�̎�E�s���p�^�[���v�̓f�[�^���Â��̂ł��̂܂g���Ȃ��D
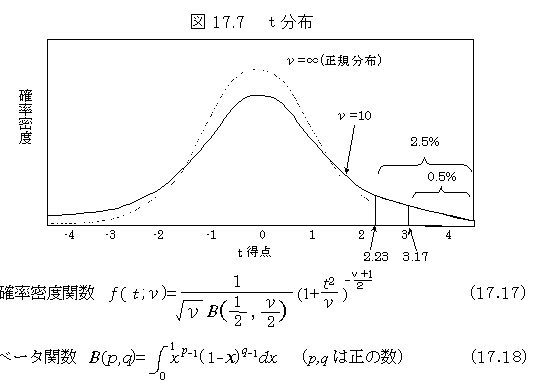
������t test
���v�I�ȉ�������@�̈�D�Q�̕��ϒl�̍������R���ۂ��肷��Ƃ��ɗp������D���K���z������Q�̕ϗʁi�j���Ə����̐g���̕��z�Ȃǁj�̍��̕��z�́C��W�c�̕��U���������Ă���Ƃ��ɂ͐��K���z��p���邱�Ƃ��ł��邪�C��W�c�̕��U��W�{�i����ꂽ�f�[�^�j���琄�肵���l�i�s�ΐ���l�j��p����Ƃ����z�ɂȂ�D�W�{����C���ϒl�̍��̌��������Ƃ��ɂ́C�����z�̊m����p����D
���\�i���̃p�[�Z���g�_�̕\�j
��ʂɁC������̂Ƃ��̊m�����v�Z���邱�Ƃ��ł��Ȃ��ꍇ�ɁC���\��p���ėL�ӂ��ǂ����肷��D�悭�p������T����P���ɂ��Ă̂��̒l���f�[�^��(���R�x�j���ƂɈꗗ�\�ɂ������́D
�f�[�^���͖@�i���v�w�j
���v�I���͂�����Ƃ��̊�{�I�ȍl�����i�Ȋw�I�Ȑ��_�C�v���z�u�C�f�[�^�C���[�W�Ȃǁj������D�㔼�̓R���T���^���g�̍�ƕ��S�̎d���Ȃǂ̎�����������Ă���D�uA-06 �f�[�^���͖@�v�i���v�w�j�D
�f�[�^�ϊ�
�f�[�^�̕��̓\�t�g���قȂ��Ă��邽�߂ɁC�\�t�g�ɍ��킹���f�[�^�`���ɕϊ����ĕ��͂���DEBCDIC�R�[�h��A�X�L�[�R�[�h�Ȃǂ̌v�Z�@���̕\���`���̈Ⴂ�����łȂ��C�p�\�R���Ŏg���Ă���A�X�L�[�R�[�h�ł����Ă��\�t�g�E�G�A�ɂ���āC�f�[�^�̌`�����قȂ��Ă���D�\�t�g�E�G�A�͂��ꂼ������������Ă���̂ŁC�����������Ǝ��̃f�[�^�`�����g���Ă���D��{�����̏��݂̂�\�������̂��e�L�X�g�`���ł���C�قƂ�ǂ̃\�t�g�E�F�A�̓e�L�X�g���݂̂������o����悤�ɂȂ��Ă���D�����̋��ɃJ���}�i�C�j��p������C�^�u��p������i�X�y�[�X�j����D���L����p���Ȃ��ŏc�����ɔ��p�X�y�[�X�Ŗ��߂邱�Ƃ�����D�f�[�^��K���ȑ傫���ł܂Ƃ߂āC���R�[�h����邱�Ƃ�����D���[�v���ł͂P���R�[�h�͂P�s�ɑΉ�����D�s�̋��́C�e�e�R�[�h�i���C���t�B�[�h�j�Ƃb�q�R�[�h�i�L�����b�W���^�[���j�����邱�Ƃ������̂ŁC�قƂ�ǂ̃\�t�g�E�F�A�́C�e�e�Ƃb�q�̓C���[�W�I�ȉ��s�ƈ�v����悤�ɍ���Ă���D���v���͂ł́C�e�L�X�g�`���̃f�[�^���т�G�N�Z�����[�N�V�[�g�̂悤�ȕ\�ɕ��ׂ��ꂽ�f�[�^�͉\�Ȍ`���ɕ��ׂȂ�������C�ꕔ�������o�����Ƃ������D��̓I�ɂ́C���l�߂ɓ��͂��ꂽ���d���ڂ��O�P�`���ɕϊ�������C�����̉��ɕ��f�[�^�����̍��ڏ��ɕ��ׂȂ�������C�Ґ��̏��Ȃ��J�e�S���[���R�~�ɂ��ĐV�����J�e�S���[���������C�N��̂悤�Ȏ������������̃J�e�S���[�ɕ��ނ����肷��D
�e�L�X�g�}�C�j���O
�e�L�X�g�f�[�^���@��N�������ƁD���͂̃f�[�^�v�I�ɕ��͂���ꍇ�ɂ��g���邱�Ƃ�����D
�K���
�����Q�[���\�t�g�B
�f�U�C���C���[�W�]��
�p�b�P�[�W�f�U�C���ȂLj�ʏ���҂̃f�U�C���v�f�ɂ��ẴC���[�W�]���𑪒肷����@�D��{�I�ɑ����̕]���̍��ڂɂ���āC�]���������ʂ���ԓI�Ɉʒu�t����D���ϗʉ�͂����Ȃ��ŁC�����̋�ԂɈʒu�t������@�i�e�X�g�`���C�O�����́j�ƁC���̓s�x���͂����āC�I�����ꂽ�]���Ώہi�C�{�[�NăZ�b�g�j���o�����X�ǂ��z�u��������@������D
�f���t�@�C�@
���ƂȂ��Ă���̈�̐��Ƃ����āA���̌��ʂ��܂Ƃ߂邱�Ƃɂ���ė\�����s�����@�D���Ƃւ̒������n���I�A���ʓI�ɍs���悤�Ȑ��i�����D�قڑÓ��ȗ\���������邪�C�ӎ������Ȃ̂ŁA���s�I�Ȍ����ɂȂ�ꍇ������D��ʓI�Ȍ��������Ɠ��l�A�����ʂ���̃A�v���[�`�ƕʂ̏��̗\���ƕ��p���邱�Ƃ��K�v�ł���D
�W�J�@unfolding method
�@�����̎h���Ԃ̋�����ގ��x�̃f�[�^����A�h���̎ړx�l�i���W�l�j�����߂���@���A�S���ړx�\���ƌ����邪�A�������̋�ԓ��̎ړx�l�i���W�l�j�����߂�ꍇ�́AMDS�i�������ړx�\���@�܂��͑������ړx�@�j�ƌ�����B��ʂɁA�ގ��x�s��̍s�̗v�f�Ɨ�̗v�f���قȂ����h���̏ꍇ�i�Q���Q���f�[�^�ƌ�����j�̎ړx�\���@���W�J�@�ƌĂ�Ă���B�����́A�ړx��̍��E�ǂ���ł��������l�ŕ\������邪�A�����̎h���Ƃ̊W����A�h�����E�⍶�ɕ����Ă����i�W�J����j�Ƃ����C���[�W����W�J�@�Ɩ��t�����Ă���B�N�[���̓W�J�@�A�V�F�[�l�}���̌v�ʓI�W�J�@�Ȃǂ�����B��ԕz�u�����܂��Ă���h���Ƃ̗ގ��W�𑪒肵�āi�s��̕Е��̗v�f�̎ړx�l�����܂��Ă��邱�Ɓj�A�W�J�@�I�ȕ��͂�����O���W�J�@������B�ŋ߂ł́A��Ώ̍s��̊֘A�x�̕��͂Ƃ��āA�x���[�N���̃R���X�|���f���X���́A�������֕��͂Ȃǂ��A�W�J�@�Ƃ̊W�Ŏ��グ���邱�Ƃ������B
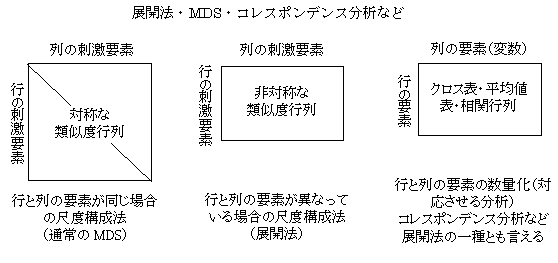
�W�J�@unfolding method�ƃR���X�|���f���X���͂Ƃ̊W
�@�ގ����̃f�[�^�ɂ��āA�s�v�f�Ɨ�v�f���قȂ����ꍇ�̐��ʉ�����i�ړx�l�����߂�j���@�ł��邱�Ƃ���A�R���X�|���f���X���͓͂W�J�@�̈��ł���ƌ�����B�������A�R���X�|���f���X���͂́A�s�v�f�Ɨ�v�f��Ή�������Ƃ����ړI�����邱�Ƃ���A�s�Ɨ�Ƃ��قȂ����W���̗v�f�ł���ꍇ�̕��͖@�Ƃ��čl����ꂽ�̂ŁA���ʎړx���W�����_�ɂȂ�̂ŁA��Ԃ�����l�̒P�ʂƌ��_�Ƃ͈قȂ��Ă��邱�Ƃ�O��Ƃ��Ă��鑽�ϗʂ̉�͖@�ł���B���������āA�s�v�f�Ɨ�v�f�Ƃ�Ή������邽�߂ɂ́A�W�������ꂽ��̎ړx�l���p������B�N���X�\�̏ꍇ�A�|�A�\�����z��z�肵�āA�S�̐����A��̎���ʁA�s�̎���ʂ������A�s�v�f�Ɨ�v�f�̊֘A���̕����݂̂����o���āi�J�C�Q�擝�v�ʁj�A�����k���̕��͂��s���i�听�����́j�B�W�J�@�́A�s�v�f�Ɨ�v�f�Ƃ̊֘A���ڑ��肵���ƍl����̂ŁA����l���̂��̂��g���Ă��̂܂ړx�l�����߂�B���������āA�W�J�@�̍l�����ł́A��Ώ̂̃f�[�^�s��̐��l�����̂܂ړx�l�ɕ\������邪�A�R���X�|���f���X���͂ł͑���l���̂��̂̌X���ł͂Ȃ��A�֘A���s��i���ݍ�p�ɓ�����j�������k���̕��͑ΏۂɂȂ�B
�X�ܕ]�����f��(���Ђ̕��̓V�X�e���j
�����̓X�܃f�[�^�̕]�����ʂ���\�����ꂽ�������ɂ���āC�X�����ɂ���āC�\�z����闈�q���┄�㍂���v�Z����V�X�e���D�v���̃J�e�S���[�E�F�C�g���v�Z���Ă����ĊY������v�������̐��l���o�͂���D�v�i�K�ł��������̔���Ȃǂ̂��������̈ʒu�Â���������̂ŕ֗��Ȕ��ʁC�l������Ȃ��v�����傫����p����Ɨ\�������D�l������Ȃ��v���Ƃ́C���s��o�ϗv���Ȃǂ̊O�I�̂ق��C�n��̂��ŗL�ȃC���[�W�Ȃǂł����ʉ����ɂ����v���ł���D
�����W�c����̔䗦�̌���
����������Ȃǂ����āC��̎��⍀�ڂ́u�͂��v�u�������v�̊����̍������肷��悤�ȏꍇ�D�ʂ̍��ڂ̍��͑Ή��̂����̍��̌���C�����ȂǕʂ̏W�c�Ԃ̔�̍��ȂǂƂ͌���@���قȂ�D�u�͂��v�u�������v�̍��́C�A��������50%�̉��ɂȂ�D������W�c�Ȃ̂ŁC�f�[�^��߂��߂��Ȃ��̖��͂Ȃ��C�Q���m�����g����D������W�c�ɑΉ������x����傫�Ȑ����Ƃ��ē��͂���C�ߎ��I�ɒ����z�̊m���ł�����ł���D�v�Z�͌v�Z�@������Δ�r�I�ȒP�Ɍv�Z�ł��邪�C�m���傫���Ƃ��ɂ͐��K���z�̊m���ƂقƂ�Lj�v����̂ŗ��p�ł���D�m���������ꍇ�ɂ́C���łɌv�Z����Ă���Q���m���̕\�𗘗p���邱�Ƃ��ł���D�J�e�S���[���R�ȏ�̏ꍇ�ɂ́C�������z�̊m���ɂȂ�D���̏ꍇ�C�m���傫����J�C�Q�挟�肪���p�ł���D��͂�C�ߎ��I�ɒ����z�̊m���ł��v�Z�ł���D
�g�[�K�[�\���̌v�ʓI�l�c�r�iTorgerson's metric�l�c�r�j
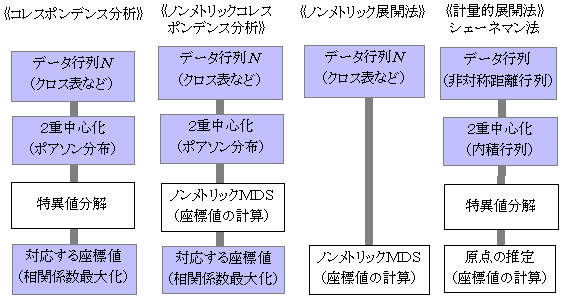
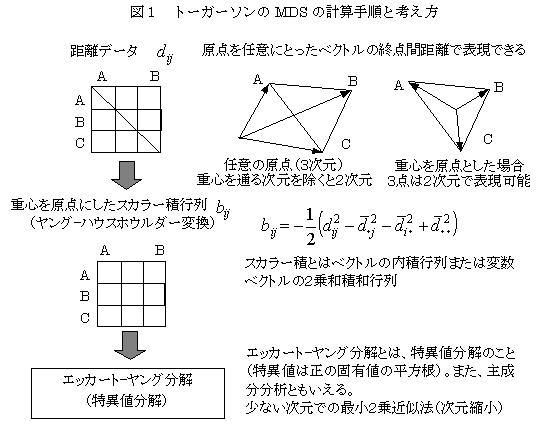
�@MDS�i�������ړx�\���@�Amultidimensional scaling�j�́A�h���Ԃ̍��فi�����j���瑽�����̎ړx�l�����߂���@�ł���A�ϐ��Ԃ̑��֊W�͂��鑽�ϗʉ�͂ƈقȂ��Ă��邪�A�����悤�Ȍv�Z�@�ɂȂ��Ă���B����Ȍ�ɊJ�����ꂽ�m�����g���b�NMDS���h���Ԃ̗ގ��W�̏������͂���̂ƈ���āA�g�[�K�[�\����MDS�́A�����͑ΏۂƂ���B�g�[�K�[�\���́C���_�����肳��Ă��Ȃ��h���Ԃ̋�������A�d�S�����_�Ƃ���x�N�g���̓��ρi�X�J���[�ρj�ɕϊ����i�����O-�n�E�X�z�E���_�[�̕ϊ��j�A����ɁC�G�b�J�[�g-�����O�����i���ْl�����̂��ƁE�Ϙa�̎听�����͂Ɠ����j�ɂ���č��W�l�����߂���@���������B�听�����͂��番����悤�ɁA�����������݂̂�p����A�c��̕��U���덷���邢�͕K�v�Ȃ������ƍl���āA�����������ŋߎ����邱�Ƃ��ł���B�R�_�Ԃ̑��݂̋�����������������l�ɂȂ邱�Ƃ������̂Łi���̐}�Q�Ɓj�A�萔�����Z���āA�������������Ȃ���Ȃ�Ȃ��B�v�Z�@�����ْl��������{�ɂ��Ă��邱�Ƃ���A���̑��̑����̕��͖@�Ƌ��ʓ_�������Ă��邪�A���ْl�����̑O�̋����𑪒肷�邱�ƁA���Z�萔�A�����O-�n�E�X�z�E���_�[�ϊ��Ƃ����葱���������I�ł���B�l�Ԃ̑����̍s���ł́A���������Ă͂܂邱�Ƃ����Ȃ��A�܂��A�v�ʓI�l�c�r�ł͑����̎�����K�v�Ƃ��邱�Ɓi�Q�����̋ߎ��ɖ��������邱�Ɓj�Ȃǂ���A���p���₷���m�����g���b�N��MDS���L���g���Ă���B
���v�I��������
�f�[�^�Ɍ�����X�������R�ɋN���������ƂȂ̂��ۂ��肷����@�D��ʓI�ɁC���̃f�[�^�������W�c���璊�o����āC�{�������Ȃ��̂ɁC���R�̗��ꂽ�f�[�^���I�ꂽ�ƍl���āC���̂悤�ȍ����N����\���̓x�����v�Z����D���R�ɂ��Ă͒��������Ƃ��N���������ƂɂȂ�����C���R�Ƃ͍l���Ȃ��ňقȂ�����W�c����I�ꂽ�ƍl����D�ɂ߂Ē��������Ƃ̓x���Ƃ��ĂT���܂��͂P���̊m����p���邱�Ƃ������D���R�ɋN���������Ƃ�O��ɂ���̂ŁC�f�[�^���W�߂�Ƃ��C��{�I�ɕ�W�c����̖���ג��o���邱�Ƃ��d�v�ȗv���ɂȂ�C�f�[�^�̐��͑����������o�͂������D�f�[�^�����Ȃ��ƁC���R�ł͂Ȃ��Ƃ������_���o�ɂ����D�p����m�����z�̓f�[�^�̐����ɂ���ĈقȂ邪�C��2���z�C�����z�C�e���z�C���K���z�Ȃǂ̂ق��C�����鎖�ۂ̋N���蓾��ꍇ�̐����v�Z���āC���N�������ۂ̊m�����v�Z����悤�Ȍv�Z�@������D�Ȋw�I�Ȍ��_���o���Ƃ��ɁC�d�v�Ȗ���������{�I�ȍl�����ł���D�L�Ӑ�����ƌ������Ƃ�����D
�����̃C���[�W�}�b�v
�����̃C���[�W�ɂ��ẮC�uJ-17���q���͂ƃR���X�|���f���X���͂ɂ��C���[�W�̑���@�vA5��220�y�[�W�A5000�~�A�Q�Ɓi�J���[����ł͂���܂���j�B���U�E�����U�s��̎听�����͂���q���͂ɂ��ẮC�u�f�[�^���͓���vA5��320�y�[�W�C5000�~�C�Q�ƁD
���ْl����singular value decomposition
�����Ȃǂɂ���ē���ꂽ�����̃f�[�^�x�N�g���́A�����������̍��W�l�ŕ\�����邱�Ƃ��ł���B��Ԃ̑��ΓI�Ȉʒu�W�́A�f�[�^�ɂ���ČŒ肳��邪�A���W���́A��ӂɌ��߂��Ȃ��B�����ŁA�f�[�^�̕��U�i�Q��a�j���ł��傫���\������悤�Ȏ��i�厲�j���������߂邱�Ƃɂ���ƈ�ӂɎ������߂邱�Ƃ��ł���B�f�[�^�s������̂悤�Ȏ��̍��W�l�Ƃ��ĕ\�����邱�Ƃ́A�f�[�^�������̎����ɂ���ċߎ����āA�ϐ��x�N�g������ԓI�ɕ\������Ɖ��p�I�ɕ֗��ł���i��̓����̐}�Ȃǁj�B�܂��A�����̂���ݓI�Ȉ��q�ƍl���āA�����I�ȑ��茋�ʂ̌�����T�邽�߂ɗL���Ȏ�i�ɂȂ�B���̂悤�Ȓ����������̍��W�l���ŗL�x�N�g���ł���A���������U�̑傫�����ŗL�l�ɂȂ�B�ŗL�l�ɕ��U�̑傫���f������̂ŁA�ŗL�x�N�g���́A�Q��a���P�ɂȂ�悤�ɐ��K�����āi���U�̑傫���������āj�\�����邱�Ƃ���ʓI�ł���B�G�b�J�[�g�E�����O�����ƌ����邱�Ƃ�����B
�@���֍s��̂悤�ɕ��U�i�Q��a�j���ŗL�l�E�ŗL�x�N�g���ŕ\������ꍇ�i�X�y�N�g�������j�́A�f�[�^�s��̕Е��̗v�f�̕����݂̂�\�����A�ŗL�l�����U�̎����ł̐�������\�����Ă���B���ْl�����́A�Q���\�̏ꍇ�ɗ�����A�s�����̌ŗL�l�i�����j�������ɂȂ邱�Ƃ���i�o�ΐ��j�A�f�[�^�s����A�s�v�f�̌ŗL�x�N�g���A��v�f�̌ŗL�x�N�g���A�ŗL�l�̕������i���ْl�j�ɂ���ĕ�������`���ɂȂ�B���ْl�������A�R���ȏ�̃f�[�^�Ɉ�ʉ�������������@canonical
decomposition����������B

�Ɨ��ϐ�independent variable
�\��������Ƃ��ɗ\�����鑤�̕ϐ��D��ʂɁC������\�������ϐ��Ȃ̂ŁC���̕ϐ��Ɉˑ����Ȃ��Ƃ����Ӗ��Łu�Ɨ��ϐ��v�ƌ�����D�����ɁC�d��A���͂Ȃǂɗp������D���̂ق��C�u�����ϐ��v�C�u�v���v�Ȃǂ̗p��͓����Ӗ��Ɏg���邱�Ƃ����邪�C�����ϐ���v���Ƃ����p��́C�ϐ����Ɨ��i�{���݂����֊W�������Ȃ��j���Ă��Ȃ��ꍇ�Ɏg�p���邱�Ƃ��ł���D�\������鑤�̕ϐ��́C�]���ϐ��C������ϐ��C�ړI�ϐ��C����l�C�O�I��Ȃǂƌ����邱�Ƃ�����D
�s�s���]���C�s�s�����̉��K���C�s�s�̕���(���Ђ̕��̓V�X�e���j
�Z���̈ӎ������ɂ��s�s�̕]���͒ʏ�̃A���P�[�g�`���ɂ���đ���ł���D�l���i��ԁC���ԁj�Ȃǂ̋K�͂�{�݂̌���L���C�X�є_�n�Ȃǂ̖ʐρC��l������̏��ʐςȂǂ̏Z���w�W�ȂǁC���v�����Ɋ�Â����s�s���̕]�����\�ł���D�uJ-34�s�s�]���v�ȂǎQ�ƁD
�g���[�h�I�t�@trade-off method
�R���W���C���g����̎��C�Q�̗v���̑g�ݍ��킹���h���ɑ��āC��Δ�r�`���ŁC�ǂ��炩��I�ԂƂ����ۑ���n���I�ɐi�߂邱�Ƃɂ���āC�h���������Â�����@�D�y�A���C�Y�@�Ƃ�������D���Ђ̃\�t�g�̓G�N�Z����œ����i�摜�\�j�C�R���W���C���g�V�~�����[�V�����ƘA������Ă���D���i�ƃu�����h�ɓ��肵���]���\�t�g������D�i�u�����h���C�����e�B�̉��i�ɂ�鑪��Ȃǁj
Home�@���������@��ЊT�v�@�A�s�@�J�s�@�T�s�@�^�s�@�i�s�@�n�s�@�}�s�@���s�@���s�@���s�@�Q�l����