Home�@���������@��ЊT�v�@�A�s�@�J�s�@�T�s�@�^�s�@�i�s�@�n�s�@�}�s�@���s�@���s�@���s�@�Q�l����
�ŏ��Q��@ least square method
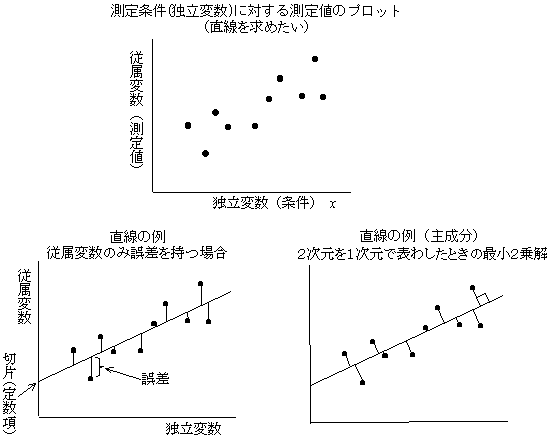
�@����̑�������i�Ɨ��ϐ��̒l�j�ɑΉ����đ���l�������A�����I�W������Ƃ�(y=ax+b)�C�����̈ʒu�����߂����i���̐}�Q�Ɓj�B���Ȃ킿�Aa�Cb�����߂����B�_���Q�ł���ΘA���������ɂ���Ē��������߂��邪�A�_�������ꍇ�ɂ́A�A���������ł͌��߂��Ȃ��B�f�[�^�ɑ���덷������̂ŁA�Q�_���璼�������߂���́A�����̓_���璼�������߂�����悢�B�ڂŌ��āA�����������Č���ƁA�����̗�̐}�̉E���̂悤�Ȓ����������Ă��܂����Ƃ������i�听���j�Bx�ɂ͌덷���Ȃ�y�����̂덷������̂ŁA�����̗�̐}�̍����̂悤�ȈӖ��ł̐^���ɒ��������������B�ŏ��Q��@���悭�p������B
�@���̏ꍇ�̍ŏ��Q��@�i��A���́j�́Ay�������̌덷���ŏ��ɂȂ�悤�Ȓ����ł��邪�A�ʂ̌�����������ƁA���ׂĂ̓_����̋������ł��������Ȃ钼���i�߂������j�ƌ�����B�v�Z�@�́A����l�Ɩ��m�����܂��_�l�Ƃ̍��̂Q������v���A���̍ŏ��l�����߂�B�Q��͂Q�����ł���̂ŁA�ŏ��l�����߂�ɂ͊e�ϐ����Ƃɔ������āi�Δ����j�O�ɓ������Ȃ�ꍇ�i�ڐ��̌X�����O�j�ł���B�ϐ��̐����������ł��A���ׂĂ��O�ɂȂ�ꍇ�ł���̂ŁA�P���̘A�����������������ƂɂȂ�B�E���̐}�̎听���́A�����̕ϐ��Ɍ덷������ꍇ�ŁA�Q�����i�Q�ϐ��j���P�����ŋߎ�����Ƃ��̍ŏ��Q����ɂȂ�B

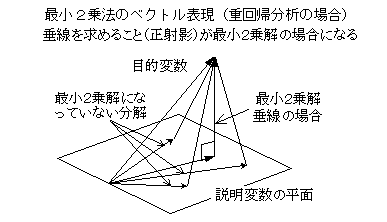
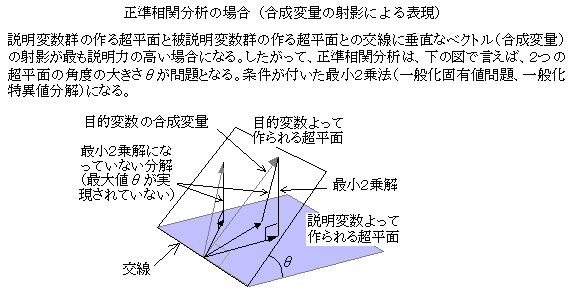
�d��A���͂̏ꍇ�i�Ɨ��ϐ��������̏ꍇ�j�A�x�N�g���ŕ\������A�ړI�ϐ�����A�Ɨ��ϐ����ʁi��ԁj�ɐ��������낵���Ƃ��i���ˉe�j�A�ŏ��Q����ɂȂ�B�Ɨ��ϐ���Ԃւ̎ˉe�́A�����ɂ��邪�A�����͂P�����ł���A����́A�ŒZ�����i�ŏ��덷�j�ł�����B�ړI�ϐ�����������Ƃ��ɂ́i�������֕��́j�A�ړI�ϐ���Ԃ���Ɨ��ϐ���Ԃւ̐��ˉe�ɂ���āA�ŏ��Q�����������B���̏ꍇ�A�Q�̋�Ԃ̂Ȃ��p�ɐ������W�����\������Ă���i�����]���j�B�Q�̋�Ԃ̂Ȃ��p�́A��Ԃ����ꂼ�꒴���ʂŕ\�킷�ƁA���ʂ̊p�x�ł���A����Ɛ����ł��ꂼ��̕��ʂɊ܂܂��x�N�g���̂Ȃ��p�ł�����i���̐}�j�B�����̃x�N�g���́A���ꂼ��̕��ʂ��\������ϐ��̍����ϗʂł���A�����ϗʊԂ̑��ւƂ�������B�����̍����ϗʂ́A�݂��ɐ��������낵���ꍇ�A����́A�ŏ��Q����Ƃ��āA�Q�Q�̍����ϗʊԂ̍ő�̐������W����\�킷�B
�Ŗޖ@maximum likelihood method
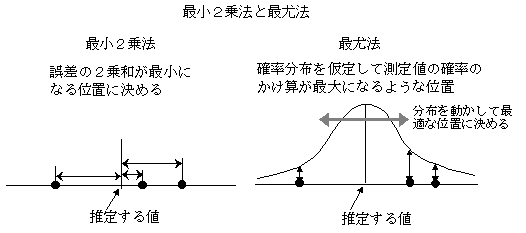
�@�ŏ��Q��@�́A�����̑���l���璆�S�I�Ȉʒu�Ⓖ�������߂�v�Z�@�ł��邪�A�Ŗޖ@�́A�m���I�ɍł��m���炵���l�𐄒肷����@�ł���B����l�Ƃ��Ċm���炵�����肪����ɂ��邱�Ƃ͏d�v�Ȃ��Ƃł���B�������A����덷�ɐ��K���z��z�肵���ꍇ�ɂ́A�ŏ��Q�搄��l�́A�Ŗސ���l�i�m���I�ɍł��m���炵������l�j�ɂȂ��Ă���B�ŏ��Q��@���A����l�̏�琄��l�����߂邪�A�Ŗޖ@�́A����l�ɑ��āA�m���I�Ȋm���炵���i�m�����z�j��z�肵�āA���̏�琄��l�����߂�B���������āA����l�̌덷�Ɋm�����z��z�肵�Ȃ���Ȃ�Ȃ��B�v�Z�葱���́A����l�ɑΉ�����m���i�m�����x�j�����ׂĂ̑���l�ɂ��Ċ|�����킹�āA����l�S�̂̊m���炵�������߂�B�|�����킹��̂́A�Ɨ���������l�̊m���ł��邩��A�S�̂̊m���͊|���Z�ɂȂ�B�m���ɂ́A���߂�ׂ����m�����܂܂�Ă���̂ŁA���̌`���ɂȂ��Ă���i�ޓx���j�A���z�͌Œ肳��Ă��Ȃ��i���̐}�Q�Ɓj�B���̐}�ł́A���z�����E�ɓ������āA�R�̑���l�̊m���̊|���Z�l�i�ޓx���j���ő�ɂȂ�ʒu�ɕ��z���Œ肵�āA���̂Ƃ��̒��_�̈ʒu������l�ɂȂ�B���K���z�ȊO�̏ꍇ�ɂ́A���߂関�m���i���m�ꐔ�j�͕��z�̍ł��������Ƃ͌���Ȃ��B�ǂ̈ʒu�ɕ��z���Œ肷�邩���Ŗޖ@�̖ړI�ł���B���z���ړ�����ƁA����l�̊m���i�c�����̊m�����x�j�̊|���Z�l�͕ω����邪�i�ޓx���j�A���̍ő�̏ꍇ�́A�m�����ł������l�Ȃ̂ŁA�ł��m���炵���ꍇ�ƌ�����B���̏ꍇ�̖��m�������߂�悢���ƂɂȂ�B
�@��̓I�Ȍv�Z�ł́A�|���Z�̌`���̖ޓx��ΐ��ɕω�����Ɓi�ΐ��ޓx���j�A�召�W�͖ޓx���ƕς�炸�C�����Z�̌`�ɂȂ�̂ŁA�ΐ��ޓx�̍ő�l�����߂�B���ϐ��̏ꍇ�ɂ́C�ϐ����ƂɕΔ������āA�A�����������������ƂɂȂ邪�A����`�̐���l�ɂȂ邱�Ƃ������B�قƂ�ǂ̏ꍇ�A���z�Ƃ��āA�w���^���z�i���K���z�A���z�A�|�A�\�����z�Ȃǁj��z�肷��̂ŁA�v�Z�@�ɋ��ʂ��������������B
��Ǝ�̌����i���Ђ̌����ۑ�j
�@�A�Ɗ��̕ω��ɔ����A��ƈ��̓K�����l����Ƃ��C�Ǝ��E��Ƃ͕ʂɁC��Ƃ̓���i�R���s���[�^�Ȃǁj��l�ԊW�̓����Ȃǂ��d�v�ɂȂ��Ă���D���̓����́C�L���Ӗ��̐l�Ԃ̐��i��\�͂̕��ނɋ߂��̂ŁC�l�Ԃ̌����̈ꑤ�ʂƌ�����D���̂悤�ȁC��ƕ��͂����邱�Ƃɂ���Ċ��̐v���Ɗ��̐������A���K���A���Y���Ȃǂ̊����P�ɂ͕K�v�Ȃ��Ƃł���D
�T�[�X�g���̈�Δ�r�@ Thurstone's pared comparison method
�@��̎h�������̔��f��i�D�������Ȃǁj��r���āC�u�͂��v�̉�������C�ړx���_�����߂�D�S���ړx�i���f�ړx�j��ŁC�h�������K���z����Ɖ��肵�āC�u�͂��v���f�̊�������C���K�m���ɂ���āC�ړx�l�����߂�D�����ȉ��̍����ړx�l�̈Ⴂ��\���̂ŁC�ٕʂ����m�Ȏh���̎ړx�l����ɂ͎g���Ȃ��D���茋�ʂ��݂�ƁC�قƂ�ǖ����������Ȃ��̂ŁC���K���z�̉���́C�����ɋ߂����肾�Ǝv����D����l�邽�߂ɑ����̔팱�҂⑽���̑���l���K�v�Ȃ��߁C���p�I�ɂ͂��܂�g���Ȃ��D��Δ�r�@�ł́C���ʂ�]�肵�ĊԊu�ړx�Ƃ���V�F�b�t�F�̈�Δ�r�@��P��a�@�i�R���X�^���g�T���C�`�b�v�Q�[���j�̔䗦�]���@�C�]��l��{�����f���ʂƂ��ĕ��͂���`�g�o�^�̈�Δ�r�@�Ȃǂ���r�I�悭���p����Ă���D�T�[�X�g���̈�Δ�r�@�̃��W�b�g���f���ɂ��ẮA�u�d��A���̗͂��p�@�v�f�[�^���͌�����(2004.10��)�Q�ƁB���u�u���b�h���C�E�e���[�E�����[�X���f���v�Q�ƁB
�R���f�[�^ 3-way data
�f�|�^����ׂ��Ƃ��A�R�����\���ɕ\�������f�[�^���R���f�[�^�Ƃ����D��l�̕]���҂��A�������̐��i���̍��ڂŕ]�������f�[�^�ŁA���ׂĂ̕]���ɂ��đΏۂƍ��ڂ����ʂ��Ă���ꍇ�ɂ́A�R���f�[�^�ɂȂ�D���֍s�A��������ꍇ�ł���ϐ������ʂ��Ă���ꍇ�ɂ́A�R���f�[�^�ɂȂ邪�C���֍s��̏ꍇ�ɂ͍s�Ɨ����v�f�ɂȂ�̂łQ���f�[�^�ɂȂ�D�R���f�[�^���L�̕��̓��f������������o����Ă���B�R�����q���́A�h�m�c�r�b�`�k�ȂǎQ�ƁB
�R�����q���� three mode factor analysis
�@��l�̕]���҂��������̕]���Ώۂɂ��āC�������̕]���ړx�i���ځj�ɂ���ĕ]�������f�[�^�́C�R���f�[�^�ƌ�����D�]���ړx�i���ځj�̈��q�̂ق��C�]���Ώۂ̈��q�C�]���҂̈��q�Ƃ����悤�ɁC�R�̑��ɂ��āC���q�����߂邱�Ƃɂ���ăf�[�^��v�邱�Ƃ��ł���D���͌��ʂ́A���z�I�ȕ]���҈��q�����z�I�ȃC���[�W���q�ړx�ɂ���āA���z�I�ȕ]���Ώۂ̈��q��]���������ʁA�Ƃ����悤�ȉ��߂��ł���B�u�R���X�|���f���X���̗͂��p�@�v�ȂǎQ�ƁB���̐}�ł́A�u�����h�݈̂��q�ɂ��Ă��Ȃ����͗�ł���B�����ł̐����ł́A�^�b�J�[�̊j�s�����Ɉӎ������Ɉ��q�ɂ���ėv�ꂽ���_�s��Ƃ��ĉ��p���Ă���B.
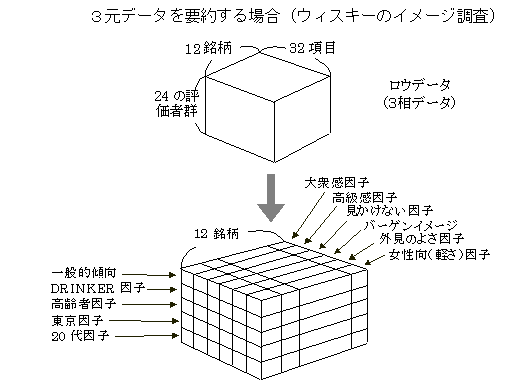
�R�����q���͂ƂR�����q����three way factor analysis
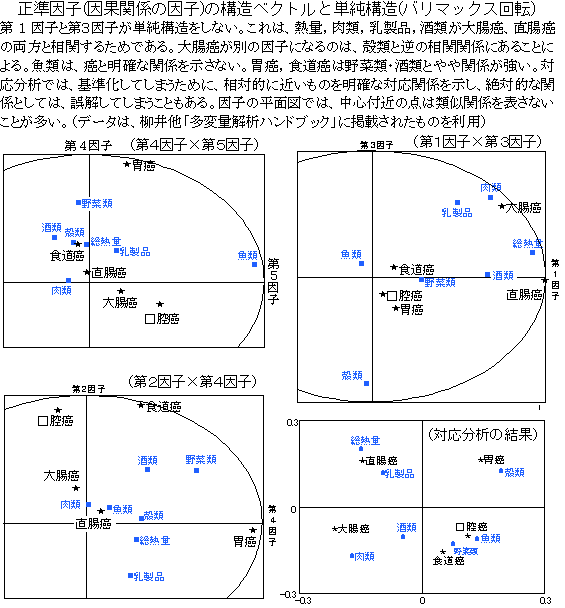
�@�{���ł́A�R���f�[�^�̂R�̑���ʁX�Ɉ��q���͂���ꍇ���R�����q���͂ƌ����A�R�̑�����̈��q��Ԃɕ\������ꍇ���R�����q���͂ƌ����Ă���B�R�����q���͂́A��{�I�ɁA�f�[�^���R�̑��̗ގ��W��\���������̂ł���K�v������i�R�d�N���X�\�Ȃǁj���A�R�����q���͂̏ꍇ�ɂ́A�ړx�~�Ώہ~�]���҂Ȃǂ̃v���t�B�[���f�[�^�i�]��ړx�Ȃǁj����ʓI�ɕ��͂����B���̋�ʂɏ]���ƁA���L�̂R���R���X�|���f���X���͂́A�������͂R���R���X�|���f���X���͂ɂȂ�A�R���听�����͂͂R���听�����͂ɂȂ邪�A�{���ł́A����̂Ȃ��ꍇ�ɂ͖��m�ɋ�ʂ��Ă��Ȃ��B�܂��A���̍l�������炷��ƁA�h�m�c�r�b�`�k�̃��f���́A�R�����q���́i�R���听�����́j�̈��ɂȂ�A�R�̑��̂����Q����v�����āA�����ԂɎh���ƕ]���҂̂Q�̑����}�b�s���O�������ȏꍇ�ɂȂ�B
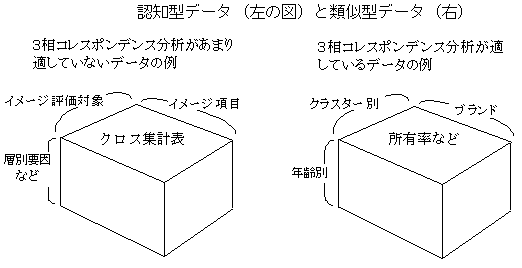
�R���R���X�|���f���X���� three mode correspondence analysis�E�R���R���X�|���f���X����
�@�ʏ�̃R���X�|���f���X���͂́C�Q�̑��̗v�f�i�s�v�f�Ɨ�v�f�j��Ή������ċ�ԏ�ɕ\��������@�ł��邪�C�R���R���X�|���f���X���͂́C�قȂ����R�����ԏ�Ɉʒu�t������@�ł���D���Ƃ��C�u�����h���L���������ʁA���l�σN���X�^�[�ʂ̏W�v���ꂽ�R�d�N���X�\�͂���ƁA�u�����h�A���L���̍����N���X�^�[�A�N���X�^�[�̑����������ԂɃv���b�g�����B�R���R���X�|���f���X���͂́A���߂�����Ȃ邱�Ƃ��������A�����R���̃R���X�|���f���X���͂ł���O���R���R���X�|���f���X�i���̒lj��@�j�̕������߂��₷�����Ƃ������B�܂��A�R���f�[�^�ɂ��ẮA��R���ڂ̗v�f�������Ƃ��āA�����Ԃɏ����ʂ̃v���b�g���ł��A�_�̈ړ��Ƃ��ĉ��߂ł��鑽�d�R���X�|���f���X���͂��g���₷���B�@�����Ŏ�舵���R�����q���͂��A���ْl�����i�ŗL�l�E�ŗL�x�N�g���j�����߂鑀���g�ݍ��킹�Čv�Z����̂ɑ��āA�R���R���X�|���f���X���͂́A���ْl�������m���f�[�^�Ɉ�ʉ���������������p���Ă���B����������canonical
decomposition�Q�ƁB�@�ΐ����`���f���̌��ݍ�p�����^�b�J�[���̃R�A�s���z�肵���R���听�����͂�K�p����R���X�|���f���X���͂�����iKroonenberg,1983�ȂǎQ�Ɓj�B���R���听�����͎Q�ƁB
�R���听������ three mode principal component analysis�E�R���听������
�@�ʏ�̎听�����͂́A�s�����Ɨ�����̎����������Ȃ̂ŁA�f�[�^�s��́A�s�����̌ŗL�x�N�g���A������̌ŗL�x�N�g���A���ْl�i�ŗL�l�̕������j��p���āA���ْl�����ŕ\���ł���B������A�R���f�[�^�Ɉ�ʉ����āA�R�̕����ɂ��Ẵx�N�g���i�ŗL�x�N�g���ɂ�����A���K�����x�N�g���Ƃ���j�ƂR���\�̌ŗL�l�ɂ����鐔�l�i�f�[�^�̂Q��a�����f����鐔�l�ŌŗL�l�ɂ�����j�ɂ���ăf�[�^��\�����邱�Ƃ��ł���i���������j�B�R���听�����͂́A�R�̑�mode��������Ԃɕ\��������@�ł���B�����ł́A�R�̑��̓��_��W�������āA�݂��ɑΉ�����悤�ɕϊ������R���R���X�|���f���X���͂Ƃ��ė��p���Ă���B
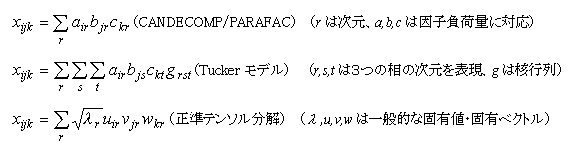
�@�^�b�J�[�n���̂R�����q���́iTucker,1966�j�ɂ����ẮA�R�̑���������ŕ\�������ꍇ�ꍇ���R���听�����͂ƌ�����i�R�����q���͈͂��q���r�I���R�Ɍ��߂āA�j�s��core
matrix�ɂ���Ĉ��q�Ԃ̊֘A����\�����郂�f���j�B�܂��A�n�[�V�}���iHarshman,1970�j��PARAFAC��L�������ƃ`�����iCarrolI&Chang,1970�j��CANDECOMP�́A�{���ł̃��f���Ǝ����I�ɓ����ł��邪�A�{���ł́A�ŗL�l�ƌŗL�x�N�g���i���ْl�����j���R���f�[�^�Ɉ�ʉ����Ă���i��ʓI�ȌŗL�l�̍��v�͂R���f�[�^�s��̂Q��a�Ɉ�v���A��ʓI�ȌŗL�x�N�g���͐��K�����s���z�肵�Ă���A�����e���\�������ƌ����Ă���j�B���R���R���X�|���f���X���́A���������Ȃǂ̍��ڎQ�ƁB
�R���f�[�^�ł��邱�Ƃ̌��������i�R�Q�̐������֕��̓f�[�^�ƂR���f�[�^�Ƃ̈Ⴂ�j
�i�R���ʃf�[�^�Ƃ̈Ⴂ�j�R���f�[�^�̓����́C�P�̑���l�ɂ��āC�R�̑���������ꍇ�ɂȂ�D�T�^�I�ȗ�ł́C����l���u�]���Ώہv�u�]���`�e���̎�ށv�u�]������l�v�ɂ���āC���肳�ꂽ�悤�ȏꍇ�ɂȂ�D����ɑ��āC�R�̑�������Ƃ��Ă��C����l���R����ꍇ�́C�P�̕]���Ώۂ��قȂ������ʁi���j����]�������ꍇ�ł���̂ŁC�P���f�[�^���R���邱�ƂɂȂ�C�R�ϗʃf�[�^���R�̑w�̃f�[�^�ɂȂ�D����l����������ꍇ�̃f�[�^�́C���ʕ��͂̂悤�ȑw�ʍ\�������f�����K�p�����̂����ʂł���D
�i���U���͂Ƃ̈Ⴂ�j�R���f�[�^�̏ꍇ�́C�`���I�ɁC���U���͂Ɠ����`�ɂȂ邪�C���U���͂Ƃ͈قȂ��āC����l�̒P�ʂƌ��_������l�ɂ���Ĉ�v���Ȃ����ƁC�����`������ϐ��̑��֊W�͂��邱�Ɓi���k��j��ړI�ɂ���̂ŁC���U���̖͂ړI�Ƃ͈���āC���ϗʉ�͂ɂȂ�D
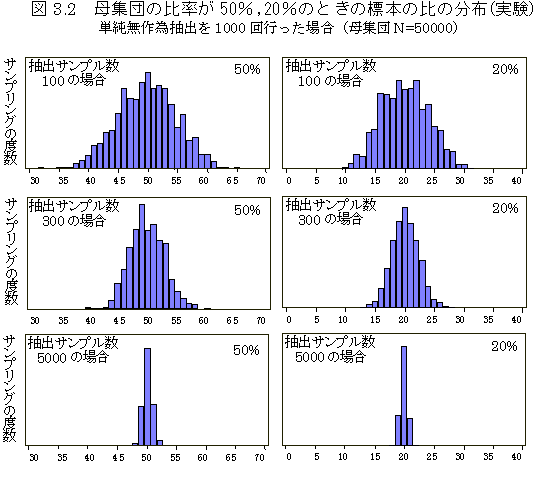
�T���v�����O�덷�i�W�{�덷)
��W�c���烉���_���ɕW�{��I��ŕ��ϒl���v�Z�����Ƃ��C�����_���ł����Ă��C���R�ɑ傫���l�����Ώۂ����I��ł��܂����Ƃ����肤��D��W�c�̐��l�����K���z�Ȃǂ̊m�����z�������_���ɑI�Ƃ���C�W�{��������C��\�����v�Z�ł���ꍇ�������D�����̃T���v�������Ă��邩���Ȃ����́C����Ȃ�����ǁC���Ă���Ƃ�����x�̒��x�ł��邩�C���̃T���v�����O�덷���Z�o�ł��邱�Ƃ������D�䗦�╽�ϒl�̃T���v�����O�덷���v�Z���鎮������i�f�[�^���͓���i�������Ёj�̑�R�͂₻�̑��̕����Q�Ɓj�D�^�̒l�������Ă�������I�ȏ�ݒ肵�āC���ۂɃT���v�����O���������Č���ƁC�قځC���_���ʂ�ɂȂ�D�P������ג��o�ł͂Ȃ��C���i���o�@��C�w�ʒ��o�̏ꍇ�ɂ́C�i�K�̓��e��w�ʂ̓��e�����m�łȂ��ƃT���v�����O�덷�͌v�Z�ł��Ȃ����C�P������ג��o�̃T���v�����O�덷�́C�T���v���̑傫���ɑ���덷�̂��������̒l�������Ă���̂ŁC�Q�l�ɂ��邱�Ƃ��ł���D
�R�ϐ��Q�̑��ϗʉ�A���������ϗʉ�A���́i�R�̌Q�̏ꍇ�j
�R�ϐ��Q�̐������֕��������ϗʉ�A���́i�R�̌Q�̏ꍇ�j
�b�u�l contingent value method
���̕]���@�D����]������Ƃ��A�������Ƃ��̑����z��A�C������Ƃ��̕��S�z�Ȃǂڎ��₵�āC���̉��l�̑傫���𐄒肷����@�D���z�I�ɏ��l���邱�ƂɂȂ�̂ŁC���z�]���@�ƌĂ��D��̓I�Ȗ�肪����ꍇ�ɂ́C����R�X�g�ƌ��т��̂ŁC����㕪����₷������@�ł���D���l�Ƌ��z�����`�ȊW�ɂȂ��ꍇ�C�����I�ȃ��f�����l����Ƃ��C���ɑ��鉿�l�̑傫���Ȃ̂��C���z�ɑ��鉿�l�̑傫���Ȃ̂��ɂ���Ď�舵�����قȂ��Ă���D��̓I�Ȑ���ȂǂƗ��ꂽ��ʂ̊��]���̏ꍇ�ɂ́C���i�̈Ӗ��̕s���萫����̏����̓����̎d���ɂ���Č��ʂ����E�����\�����傫���Ȃ�D
�V�F�A�\��
��ʓI�ɁC�}�[�P�b�g�V�F�A��\������ꍇ�ɂ́C���i�̚n�D�x�Ɖ��i�⋣�����i���l�������}�C���h�V�F�A�̑���ƁC����ɁC�s��K�́C�f�B�X�g���r���[�V�����C�m�����Ȃǂ̐��茋�ʂ�p����D�f�B�X�g���r���[�V�����ƒm�����́C���i���̂��̂̓����ł͂Ȃ��̂ŁC�w�͖ڕW�⌻���I�Ɍ��܂��Ă��܂����Ƃ������D�s��K�͂́C�����ɂ͌l�������ւ��̂Ő��肪����C�l���Ȃǂ̋q�ϓI�ȑ����l���Ɉ��̊������|���邱�Ƃɂ���Đ��肵�Ă����D���i�n�D�ƃ}�C���h�V�F�A�͎����⒲���ɂ���Đ��肷�邪�C�����̍w���s���𐳊m�ɔ��f���Ȃ����Ƃ��悭������D���i�̓����Ȃǂɂ���ނ����Ȃ����������łȂ��C�����������f���ɂ����悤�ȗ\���@�ȂǁC�\���@�̖{���I�Ȗ��Ɗւ�邱�Ƃ�����D���������āC�ł��邾�������ɋ߂��e�X�g�}�[�P�e�B���O�Ȃǂ����{���邱�Ƃ����邪�C���낢��ȉ\����z�肵���\�������邽�߂ɂ́C�������x���ł̗v�����������ă��f�����\�������������Y�I�ȏꍇ�������D�e�X�g�}�[�P�e�B���O�́C�����I�Ȍ��ʂ������邪�C��������������̂ŗ\���@�Ƃ��Ă͓�����𑽂��܂�ł���D
�V�F�b�t�F�̈�Δ�r�@�Əd��A�����@
�@�]���Ώۂ̈�Δ�r�������Ƃ��̕]�����ʂ��u���D���v�u���Ȃ�D���v�Ȃǂ̃J�e�S���[�ŕ\��������B�T�[�X�g���̈�Δ�r�@��u���b�h���[�̈�Δ�r�@�̂悤��yes�Cno�̔��肩�犄�����v�Z����̂ł͂Ȃ��A�J�e�S���[�ɂ��̂܂ܐ��l��^���Đ��ʓI�Ɍv�Z����B��ʂɁA�h���̔�r���ʂ́A�]���҂ɂƂ��Ē��x�̑召��\���ł��邱�Ƃ������̂ŁA��r�I���Ȃ��f�[�^����A�������ʂȂǂ����肷�邱�Ƃ��\�ł���A���p�I�ȕ��@�ł���i���ȋZ�A�u���\�����n���h�u�b�N�v�ȂǎQ�Ɓj�B�V���i�̖���g�p�e�X�g�ȂǏ������ʂ����m�ȏꍇ�ɂ悭�p������B
�@�J�e�S���[���𑽂�����ƁA�h���͈͂̒[�̕����̍��ق��������Ȃ��Ă��܂��Ƃ����J�e�S���[�o�C���X��������i���p��͂��܂�傫�Ȗ��ɂ͂Ȃ�Ȃ��Ǝv����j�̂ŁA����̖ړI�ȊO�́A�J�e�S���[���X�C�P�P�Ȃǂ̂悤�ɑ������Ȃ������悢�B�J�e�S���[���R�Ȃǂł́A�]���҂̒m�o�����\���ɒ��o���Ă��Ȃ��\��������B���̂ق��A�����ȑ���̏ꍇ�A�������ʂ̔�Ώ̌��ہi���ԏ��ʌ덷�j���\���ł��Ȃ����A����́A�J�e�S���[�o�C���X���������Ȗ��ł���B
�@�V���i�̎g�p�e�X�g�ł悭�p�����郉�E���h���r�������̕��͖@�Ƃ��ėL���ɗ��p���邱�Ƃ��ł���B
�@���͖@�́A�u���\�����n���h�u�b�N�v�Ȃǂɏڂ����Љ��Ă��邪�A���̕\�́A�]�����ʂ��d��A���͂ɂ���ĕ��͂���ꍇ�i���U���́j�̃R�[�f�B���O�̗�ł���i�S�̎h���̔�r�̏ꍇ�j�B���̕��@�̂悤�ɁA�d��A�������s���ƁA���̂悤�ȕ֗���������B
�@�P�l�̉҂����ׂĂ̑��r����悤�ȏꍇ���������@�Ōv�Z�ł���B
�A����ʂ݂̂Ȃ炸�A�v�����Q�ȏ゠��ꍇ�i�H�i�̖��Ƒ傫���A���i�Ȃǂ��������ꍇ�Ȃǂ̈�Δ�r�j�ɂ��A��r�I�ȒP�ɓK�p�ł���B
�B���ʁA�N��ʂȂǂ̑w�ʗv��������ꍇ�A���̗v�����ʂ͂��邱�Ƃ��ł���i���ݍ�p�Ȃǂ͂��̓s�x�K�v�Ȃ��̂�����`����j�B
�C�����l������ꍇ��v�����������Ă��Ȃ��ꍇ�ȂǁA���肵�Ȃ��Ă����肷�邱�Ƃ��ł���i�d��A���͂̕Ή�A�W���Ɠ�������@�ɂȂ�j�B

���Ԃ̊T�O
���Ԃ́A�����̕ω���ړ���\�킷�����I�\���T�O�ł��邪�A����I�Ȋ��o�ł́A�����ɕω���ړ����x�́A�����Ɋւ�炸�قƂ�Ǔ����Ɋ�����̂ŁA���̂̂悤�Ɉ��肵�Ă���B���ۂɂ́A���������ł��A���͂̈��͂�d�q�̑��x�ɋ߂��ړ��Ȃǂɂ���āA�����̕ω��i������Z���j�͈قȂ��Ă���̂����ʂł��邪�i�]���Ď��Ԃ͈��ɂȂ�Ȃ��̂����ʂł��邪�j�A����̐l�Ԃ̊��o�ł́A���̂悤�ȕω��̈Ⴂ�i���Ԃ̏ɂ��Ⴂ�j�ɂ͋C�t���Ȃ����A�����I�ɁA�V���⎞�v�̐i��̈Ⴂ�́A�قƂ�ǁA���ƍl���č����x���Ȃ����x�ł���B���̈Ӗ��ŁA���Ԃ́A�ł����肵���\���T�O�ł���̂ŁA����I�ɂ͎��̂Ƃ��ė��p����邱�Ƃ����ʂł���B�ɒ[�ȏł́A�l�Ԃɑz���ł���悤�Ɏ��Ԃ��قȂ�����邱�Ƃ��������Ă���B�����̈ړ����x�̏�����ʏ�̏����菬�����Ȃ�ꍇ�̎��ԂȂǁB
�F�ʃC���[�W
�C���[�W�̑���@�iJ-17�j�i��������5000�~�j�̐F�ʂ̌��t�̃C���[�W������i�J���[����ł͂���܂���j�D���̐}�́C�F��\��t�����ꍇ�D
���n��f�[�^�̕���
���Ђł́C���n��f�[�^�̕��͂ł́C�@�}���R�t�ߒ����f���i�w���҂̐��ځC�l���̐��ځC�E�Ƃ̐��ڂȂǁj�C�A�|�A�\���ߒ����f���i�l���̐��ځC���S�҂̗\���j�C�B���U���̓��f���Ɖ�A���f���i�g�����h�C�G�ߕϓ��C�o�ώЉ�v���Ȃǁj�C�C���ȉ�A���͂ƈړ����ρC�D���莖�ۂ̃��f���\���\���i����ҍs���̏�ԕω��ȂǁC�ی������҂̗\���j�C�E���s�������������i�̎������f���C�Ȃǂ���舵���Ă���D
�h���E���ڂ̓����}�b�s���O
���Ђł́C�@�R���X�|���f���X���͂ɂ��}�b�s���O�C�A�m�����g���b�N�W�J�@���f���i�����l�ɃR���X�|���f���X���͌��ʂ�p����MDS���́j�C�B�O���W�J�@�ɂ�镪�́C�C���q���͂�听�����͂ɂ����q���_�ƈ��q���חʃx�N�g���C�D�l�c�o�q�d�e�n���̃}�b�s���O�C�Ȃǂ̕\���@���\�D
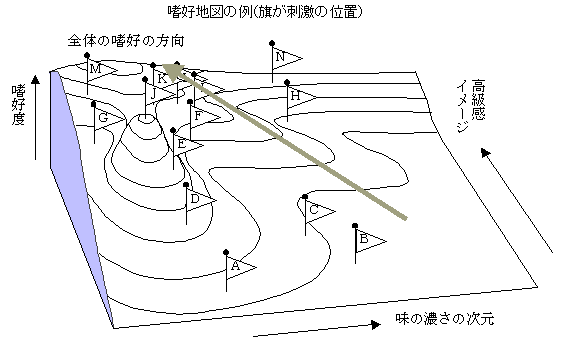
�n�D�n�} preference map
�n�D�f�[�^�̓����̏��݂̂ɂ��ٕʂɂ��}�b�v�i�������́j�Ɗ��ɂ���Ώۂ̃}�b�v�ɚn�D�X�����d�˂���@�i�O�����́j�Ƃ�����D����_�̍ł��߂��_�ɂ��O�p�`�̕ӂ̕�������{�ɂ��������n�}�쐬�@�����邪�C���p��́C�ŏI�I�ɖڂŌ��Ċm�F����K�v������ق��C���Ƃɂ��X���[�W���O���ł����p���₷���D�f�[�^����ʂɂ���ꍇ�ɂ́C�Q�����̕��z�ɂ���Ēn�}���쐬���邱�Ƃ��ł���D�}�́C�n�D�}�b�v���R�����̒n�}�̂悤�ɕ\�������ꍇ�ƂQ�����̓��n�D���i�������A���D���j�ŕ\��������ł���B
���ȉ�A
�A�����ċN���鎖�ۂ��n��Ƃ͖��W�ɋN����A�n��Ƒ���l���K�肷��v�������W�ł���Ƃ���A����l(n)�Ƃ���ɑ�������(n+1)�Ƃ͑��ւ������Ȃ��B���������āA���n��̃f�[�^������炵���f�[�^��Ή��t���đ��ւ��Ƃ�Ǝ��n��I�̌��ʂ������邱�Ƃ��ł���B���\�����̂悤�Ȑl�Ԃ̒m�o�⊴�o�̎����ɂ����ẮA���s���Ɨ��ł��邱�Ƃ͂Ȃ��A�K���A�ȑO�̎��s�̌��ʂ����o�����B�l�Ԃ̎��n����ʂɂ́A�h�����̂̎c�����ʂ̂ق��A�������J��Ԃ��Ȃ��Ƃ����悤�Ȕ����s���̎��n����ʁA�c�����ʂ��L������邱�Ƃɂ��n����ʂȂǂ����邱�Ƃ��m�F����Ă���A�d���̎����ł́A�Q���s�O�in-2�j�܂ł̎h�����ʂƉ��ʂ����邱�Ƃ�����Ă���B
�w���^���z�� exponential family of distributions�Ɛl�Ԃ̍s��
���z�C�|�A�\�����z�C�w�����z�C���K���z�Ȃǂ́C���x�����Cf(x)=c(q1,���,qp)exp{t0(x)+��qjtj(x)}(q�͎��R�ꐔ��\�킷�j�̌`�ŕ\���ł��C�w���^���z���Ƃ��Ă܂Ƃ߂��C���ʂ��������������Ă���D���R�ꐔ�́C���z�����߂邽�߂ɕK�v�ł��邪�C���z�̓����i���z�̏ꍇ�����̌��܂����Q�̏�Ԃ��畜�����ĉ������_���ɃT���v�����O����Ƃ��������j�Ƃ͖��W�Ɍ��߂���̂Łi�\�����v�ʂ����j�C���z�S�̂ɋy�ڂ��v�����ʂ�����Ƃ��ȂǕ֗��ȓ����ƂȂ�D�i���R�ꐔ�̓����𗘗p�������W�X�e�B�b�N��A���͂̐����Ȃǁj
�@�l�Ԃ̍s���ł́C�}�C�i�X�̂Ȃ��x���̌��ۂɗ��p���₷�����z���������ƁC�w���̒��̉��Z���l�Ԃ̍s�����L�q����̂ɂ悭���Ă͂܂邱�ƁC�Ȃǂ���C�d�v�ȕ��z�ł���D���i�̂P�����C�Q�����Ȃǂ̕\���́C����z�Ƃ͕ʂ̎w���̒��ł̕\���ł��邪�C���R�Ȍ`�ŕ\������Ă��邱�Ƃ́C�w���I�ȍs�����l�Ԃ��L�q���邱�ƂɗL���ł��鎖��ƌ�����D(2003.4)���u�ΐ��Ȑ��v�̍��Q�ƁD
�w����exponential function
�w�����́A���������i���͐��̒萔�j�̌`�ŕ\���ł��邪�A�l�Ԃ̍s���ɊW������́A�w�����̐}�𐬒��Ȑ��i�w�K�Ȑ��j�ƌ��������i�O�a�l�j���������P�|��-�ɂ��i�Ɂ��O,e�͎��R�ΐ��̒�j�̌`�ŕ\�����D����͎w�����z�̗ݐϊm�����z���i�b�c�e�Ccumulative
distribution function�j�ɂȂ�D�w�����͔䗦�ƊW���[���̂ōs�����L�q���郂�f���Ƃ��Ă悭���p�����D�������Ȑ��Q�ƁB
�w�����z�E�ݐώw�����z���E�w�K�Ȑ�
�w�����z�̊m�����x���́Cf(x)=exp(-��x)�̂悤�ɕ\���ł��C�ݐϕ��z���́Cy=1-exp(-��x)�ƂȂ�D�ݐϕ��z���͊w�K�Ȑ��Ƃ��Ēm���Ă���D���f���Ƃ��ė��U�ʓI�ɑ�����ƁC���x�����u���y�ʁi�w�K�ʁj�v�i�}�C�i�X�Ō����Η���ʁj��\�킷�Ƃ���ƁC�ݐϊ��i�w�K�Ȑ��j�͐ϕ��l�ł��邩��C����܂ł̕��y�ʂ̍��v�ɂ�����D���x���́C�ݐϊ��̓����i�����j�ł��邩��C���̎��_�̕��y�̑�����\�����Ă���D
���x����������K��������ƁCf'(x)=-��exp(-��x)�ƂȂ�Cf(x)/f'(x)=-���̂悤�ɒ萔�ɂȂ�D����́C���y�i�w�K��j�̑������C���X�ɒx���Ȃ��Ă������Ƃ��Ӗ����Ă���D�ʂ̌�����������ƁC��莞�Ԃ̕��y�ʁi�����E�����j���C���Ԃ��o�ɏ]���Ĉ��̊����i�Ɂj�Ō������Ă������Ƃ�\�����Ă���D
�@�悭���p������Ō����C�L���ɂ�鏤�i�̔F�m�x���C���Ԃ��o�ɏ]���āC�����������Ȃ��Ă������Ƃ������C���̊����́C�`�B��������ł���Ƃ�����C���ɒm���Ă���l�ɏ�`���\�����C���̐l���ɔ�Ⴕ�đ����Ȃ�i�����������Ȃ�j�C�Ƃ������ۂɓ��Ă͂܂�D���̂悤�Ȍ��ۂ�����Ƃ��ɂ́C�w�K�Ȑ����悭���Ă͂܂�͂��ł���D���ۂ̃f�[�^������ƁC�i�����̒ቺ�j�̌X���͎w�����z�����}�ȃJ�[�u��`�����Ƃ������D���ۓI�ɂ̓��C�u�����z�̃p�����[�^�i�x�L�w���j�ɂ���ċL�q�ł��邪�C���ۂɂ́C��Ԃ��ڍs����v�f�́C���I�Ȍ����i������\�͂Ȃǁj�ɂ���ď����̕��y���ƌ���̕��y���ł͎����قȂ��Ă���Ɨ\�z�����D���̂��Ƃ̓ɂ����ł͂Ȃ����Ƃ��Ӗ����Ă���C�l���̖�肾���łȂ��C���̌��ݍ�p�ł�������e�̋����C�V�����C�C���p�N�g�Ȃǂ��C�������Ȃ��v���ɂȂ��Ă���Ǝv����D
����ω�
�R�[�z�[�g���͂ɂ����āA�������_�̌��ʂ�\���B���`���f���̏ꍇ�A�ǂ̐���ɂ����Ă��A�ǂ̔N��ɂ����Ă��ꗥ�ɍ�p����v�����ʂƂ��đ�������B�R�[�z�[�g���͂̍��Q�ƁD
�����v�� experimental design
������uT-02�����v��E�����v��v�ł́C�����ɁC���\�����ɂ���������v�����舵���Ă���D�l�Ԃ�Ώۂɂ��������̓����Ə������ʂȂǂ̍P��덷�̎�舵���C�p�c�`�@�C��Δ�r�@�C�v���v��ƒ���\�C�a�h�a�c�C�����@�C���a�@�C���i�g�p���������C���U���͖@�Ƒ��ϗʉ�͖@�C�m���p�����g���b�N����ȂǁC�Ƃ��ɐl�Ԃ�Ώۂɂ����Ƃ��ɍl�����ׂ����_���d�_�I�ɂ��������v��̊�{�I�Ȗ���������Ă���D
�V�~�����[�V����
���ۏ�ʂɑ����đ��u�������āC���̑��u�����R�ɑ��삷�邱�Ƃɂ���āC���ۂ̏�ʂ�͋[���邱�ƁD�q��@���c�̃V�~�����[�V�����ł́C�قƂ�nj����Ɠ����悤�ȏ���邱�Ƃ��ł���ƌ����Ă���D����ҍs���̓��v�I���͂ɂ����ẮC�K���Ȑ������f����p���čw���s����\�����C�����ɂ���Đ������f���̃p�����[�^�𐄒肷�邱�Ƃɂ���āC���ۂ̐l�ԍs���̑���ɐ������f����p���čs����\�����邱�Ƃ��ł���D�R���s���[�^�̒��ɑ����̐������f����z�肵�C�V���i�Ȃǂ̓�������āC�w���҂̊������J�E���g����D���Ƃ��C����҂𐳊m�ɑ�\���������T���v���ɁC���i�̓����v���ɂ��ẴE�F�C�g�𑪒肵�Ă����C�����̈قȂ�Q�̐V���i�����ƁC�E�F�C�g�̈Ⴂ�ɂ���Ē����T���v���͈قȂ������̂�I�����邱�ƂɂȂ�D���̑I���̊������C�V���i�̑I���̗\���l�ł���D���v�I�ȃV�~�����[�V�����̐M�����͐������f���̑Ó����ƃT���v���̑Ó����i��\���j�Ɉˑ����邪�C�������f���͏œ_�����ڂ��ĒP���Ȍ`�ɂ��邱�Ƃ������̂ŁC�����T���v���̑Ó��������ʂ̗ǂ�������傫���K�肷�邱�ƂɂȂ�D
�ʐ^�ɂ��C���[�W���́E�i�ϒ���
�]�����\�Ȕ͈͂ŁC�����̎h����p�ӂł���ق��C�����v��I�ȗv���z�u���܂h���ʐ^��ݒ肷�邱�Ƃ��ł���D���͂́C���ϗʕ��U���͂�K�p����ꍇ�����邪�C���ϗʕ��U���͂̐������q��p��������C�]�����ڂ̈��q���͂ɂ�钼�����q��p��������C���p���₷�����ʂɂȂ邱�Ƃ������̂ŁC���q���́C�}�b�s���O�C�v�����͂̎菇�ŕ��͂��邱�Ƃ������D�ʐ^�h���̗v���̃E�F�C�g�����߂邱�Ƃ��ł���C�v����ω��������Ƃ��̑������i���q�j�]���̗\�����\�ɂ���D
�d��A���� multiple regression analysis�@
�w���ӌ���ړI�ϐ��i�]���ϐ��j�Ƃ���Ƃ��āC���i�ɂ��Ă̑����̃C���[�W���_��\���ϐ��i�Ɨ��ϐ��j�Ƃ����Ȃ�C���̗\��������邱�Ƃ��ł���D���`�\�������d��A���͂ɂ���č\��������́C�\���ϐ��݂̂�������C�ړI�ϐ��̒l���v�Z���邱�Ƃ��ł���D�\������������Ƃ��̐��x�Ƃ��āC�d���W���C����W���Ȃǂ�����C�\���ϐ��̌W����Ή�A�W���Ƃ����D�d��A���͂̉��p��̖ړI�́C�Q�ɕ������D��́C�{���C�Ɨ��ϐ�����������Ƃ��đ��֊W�i���ʊW�Ȃǁj�������Ȃ����C�����⒲���̓s���ŁC��������A���ւ������Ă��܂��ꍇ�ɂ́C�d��A���͂ɂ���ēƗ��ϐ��̑��ւ��������Ƃ��̉e���͂��p������D���̏ꍇ�ɂ́C�Ή�A�W���͂��̂܂܉��߂���̂��悢�D������̉��p�P�[�X�́A�Ɨ��ϐ��Ԃɂ��Ƃ��Ƒ��֊W������ꍇ�ł���C�����ϐ��������̃C���[�W���ڂȂǂ̂Ƃ��ɂ͂�����ɂ�����B���̏ꍇ�C�Ή�A�W���́C���肳�ꂽ�ϐ��̃E�F�C�g�Ƃ͕ʂ̂��̂ɂȂ�D���Ȃ킿�C���̕ϐ������ɕۂ����Ƃ��̃E�F�C�g�ɂȂ�C�{�����ւ����Ƃ����Ɨ��ϐ������ւ������Ȃ��Ƃ��̃E�F�C�g�ɂȂ�̂ŁC���̌W�����A�����ϐ��̃E�F�C�g�Ƃ��ĉ��߂��邱�Ƃ͂ł��Ȃ��D�ǂ��C���[�W���ڂ̌W�����}�C�i�X�ɂȂ邱�Ƃ����邪�C����́C���̕ϐ������ɂ���Ίm���Ƀ}�C�i�X�ɂȂ邱�Ƃ��Ӗ����邪�C���̃C���[�W���ڂ��㏸�����鑊�ւ������̕ϐ��������ɕω�����̂ŁC���ւ������̕ϐ����o�R�����E�F�C�g�����ׂč��v����ƁC�ǂ��C���[�W���ڂ̓v���X�ɓ����Ă��邱�ƂɂȂ�D���̂悤�ȑ����I�ȉe���͂́A�P���W���̕��ɔ��f����Ă���̂ŁC���̏d��A���͂̓Ɨ��ϐ��̉e���͂�����ɂ͒P���W����p���������悢���Ƃ������D���������āA�d��A���͗\���ɗp����Ƃ��ɂ́C�덷��s���肳�̖����l�����Ȃ���C�ǂ��C���[�W���ڂ̃E�F�C�g���}�C�i�X�ō����Ă��A���̂܂܂ŗ\������������x�͏オ��D���̈Ӗ��ŁA���̓K�p�̎d���i�d��A���́j�Ƌ�ʂ��āA�u�d���֖@�v�ƌ����邱�Ƃ�����B���ɓK�p�@�ɂ����āA�Ɨ��ϐ��Ԃ̑��ւ��傫���ƁC�����Ȍ덷�ł��E�F�C�g�̐���l���傫���ω�����̂ŁC���͌��ʂ̐M�������Ⴍ�Ȃ�B����́A�����ϐ��Ԃɑ��ւ�����ꍇ�̍������ւƂ͕ʂ̖��ł���A���d�������̖��ƌ�����B���d�������̖�肩�����ϐ��Ԃ̑��֊W�̖�肩�A������̏ꍇ�ł��A���ւ̍����Ɨ��ϐ��͂ǂꂩ���\�����邩�C���q���\�����Ă���d��A���͂�����������S�ƌ�����B
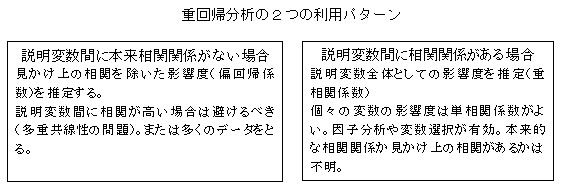
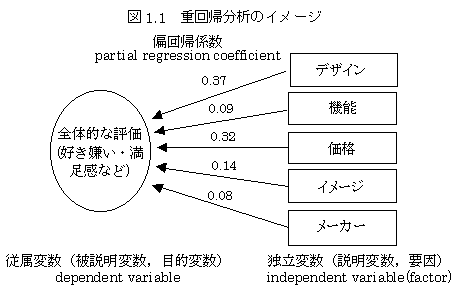
�d��A�\��
�\���ɂ͗l�X�ȕ��@�����邪�C��{�I�ɐ��`�̕������̃p�����[�^���d��A���͂ɂ���Đ��肵���Ƃ��C���̗\�����d��A�\���Ƃ����D
����W����
�ގ��x�s��s��v�f�̍��W�l�����߂镪�͖@�D�ގ��x�s��C�d�S�ϊ��������Ȃ��ČŗL�l�E�ŗL�x�N�g�����v�Z����D�g�[�K�[�\���̂l�c�r�Ɠ������@�D
�听����A
�]���ϐ�����������ꍇ�ɉ�A�\�����������Ƃ��C�X�̏]���ϐ����Ƃɉ�A���͂�K�p����ƁC�]���ϐ��Ԃ̑��ւ����邽�߂ɁC�����l�ȕ��͂��J��Ԃ��Ă����ۂ�����C�ǂ̏]���ϐ����d�v�����Ă悢�̂�������Ȃ����Ƃ�����D�{���C�d��A���͂�K�p����ꍇ�ɂ́C�]���ϐ����ړI�ϐ��Ƃ��Ĉ��肵�Ă���Ƃ��ɗp���邪�C�����f�[�^�Ȃǂł́C�]���ϐ������̗\���̂��߂̒��ԓI�ȕϐ��ł���ꍇ�������D���������āC�]���ϐ��S�̂Ƃ��Ă̊�^�x��\���͂�m�肽���Ƃ����ړI�ɂȂ�D���̏ꍇ�C�]���ϐ��̎听�����v�Z���ĉ�A���͂��s���Ə]���ϐ��̑��֊W��������đS�̂̊�^�x�������ł���D�听���͓Ɨ��ϐ��Ɩ��W�ɋ��߂���̂ŁC�Ɨ��ϐ��������v��̗v���z�u�s��i�f�U�C���s��j�̂悤�ɖ��m�Ɍv�悳��Ă���ꍇ�ɂ́C�������֕��͂�K�p��������悢���Ƃ������D�]���ϐ��̎����������ł�����q�̈Ӗ����d�v���������Ƃ��ɂ͈��q���͂ɂ����q�̒��o�Ɖ�A���͂��E�߂���D�������֕��́C�����U�\�����͂ȂǎQ�ƁD
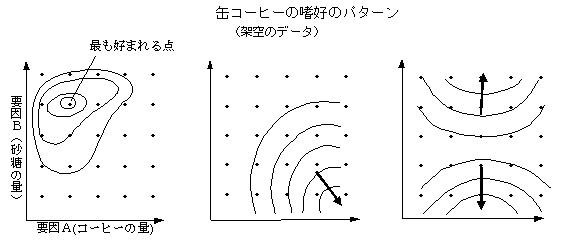
�听������ principal component analysis
���Ƃ��C�g���C�̏d�C���͂Ȃǂ̐l�̌v���l�́C���݂Ɋ֘A��������D�����̕ϐ��Ɏ听�����͂�K�p����ƁC�g���C�̏d�C���͂̂ǂ�Ƃ���v���Ȃ����C�ǂ�Ƃ��֘A���̋����听���邱�Ƃ��ł���D�听���́C����l�̒P�ʂ����ʂɂ��ĕ����̑���l�ς����悤�Ȃ��̂ł���D���m�ɂ́C�e����l�ς���̕��ɂ��ăo���c�L�����ɒ������C���d���ς������̂ł���D���d�i�E�F�C�g�j�͂R�̑���l�������Ƃ��悭�����ł���悤�Ɍ��߂���D�g�̌v���l�̏ꍇ�C��P�Ɍ��o�����听���́u���炾�̑傫���v��\�����̂ł���D�E�F�C�g�͑傫���Ɗ֘A���̍������̂قǑ傫���Ȃ�D��ʂɁC���炾���傫����C�g�����̏d�����͂��傫���D�������C�̏d�ɂ́C�ʂ̗v�f���܂܂�Ă���D�̏d�̂����C���炾�̑傫������\�z�����̏d�����d����C�����Ă���Ƃ����C���炾�̑傫������\�z�����̏d��菭�Ȃ���Α����Ă���Ƃ����D���Ȃ킿�C�̏d�̑���l����C�g�̂̑傫���v���i��P�听���j�̗v�f�������C�g���⋹�͂ɂ��Ă̓��l�ɑ傫���v���������ƁC�c��̑���l���狤�ʂ����听�������o���Ƒ�Q�听�������߂邱�Ƃ��ł���D�g�̌v���̏ꍇ�C�������������Q�听���ɂȂ邱�Ƃ������D��Q�听���̓��_�́C�傫���v���������Ă���̂ŁC�����̑����̓��_�ƌ�����D���֍s��̎听�����͂ł́C�݂��ɓƗ������听�����i�ϐ��|�P�j�i�����N�j���o�����Ƃ��ł���D�l�X�Ȕg���̗v�f���܂܂�Ă��鉹����̂ɂ��āC�����g���̗v�f�����o���X�y�N�g�����͂��听�����͂Ɠ������@�ł���D
���ʂ̈�v������
�����̐l�̏��ʕt���̌��ʂ���v���Ă��邩�ۂ��̌���D��v���Ă��Ȃ��ꍇ�ɂ́C�O���[�v���Ȃǂ̍l�����K�v�ƂȂ�D���P���h�[���̏��ʂ̈�v������ȂǁD
�������� ordinal effect
�l�Ԃ�Ώۂɂ��������̏ꍇ�C�K���������ʂ��l������K�v������D�������ʂɂ́C�n��ʒu���ʁi�P�A�̎������s�̒��̎����ʒu�C��J�C����C���ω��ȂǂƊւ��j�ƌn�ʌ��ʁi�����h�����A�����邱�Ɓj�ɕ�������D�Ƃ��Ɍn�������邱�Ƃ��K�v�ł���D�V�F�b�t�F�̈�Δ�r�@�ł́C�t�̒��̎��������ĐϋɓI�ɏ������ʂ����o���Ă���D��ʓI�ɂ͂��ׂĂ̑g�ݍ��킹����邱�Ƃ��悢���C�����K�͂ɂ�鐧���Ȃǂ�����̂ŁC�ł������u���b�N���ł̃����_�������s���悢�D���Ђł̓����_�����Ə����̑g�ݍ��킹�W�v�������O�ɍs���āC������Ă���D�������s���ꍇ�C��ƈ��ɂƂ��ẮC����Ȃ����Ƃ�����C�����_���͑傫�ȕ��S�ɂȂ��Ă���C�̊Ԉ�������D
�����ړx ordinal scale
���肳�ꂽ���l�́C���w�I�ȓ��������̂܂����Ă����ł͂Ȃ����C�ߎ��I�ɐ��w�I�ȉ��Z��K�p���邱�Ƃ��������D�l�Ԃ̍s���i���ꔽ�����܂ށj�𑪒肵�����l�́C�����Ă��鐔�w�I�ȓ����ɂ���āC���`�ړx�l�C�����ړx�l�C�Ԋu�ړx�l�C��ړx�l�Ȃǂɋ�ʂ����D���`�ړx�́C�召�W�̂Ȃ����ޒl�ŁC�w���̃N���X�����ɂP�g�C�Q�g�Ƃ����悤�ȏꍇ�ł���D�P�g�ƂQ�g�����ւ��Ă��\��Ȃ����C�`�C�a�ł��C���C��C�͂ł��{���I�ɕς��Ȃ��D�����ړx�͐��l�̊Ԋu�ɂ͈Ӗ����Ȃ��C�召�W�݈̂Ӗ��������l�D�P�ƂQ�͏����̍��ł��傫�ȍ��ł��������ʂɂȂ�D�Ԋu�ړx�͐��l�̊Ԋu�ɈӖ��̂��鐔�l�ŁC���_�ɂ͈Ӗ����Ȃ����Ɍ��߂��ꍇ�ł���D��ړx�́C���_�ɈӖ��̂���Ԋu�ړx�l�ł���D���w�I���Z�́C��{�I�ɔ�ړx�ōs����D���������āC����l���Ԋu�ړx�ł������菇���ړx�ł������肷��Ƃ��ɂ́C���ς����_�ɂ�����C���������z���Ȃ��悤�Ȏ��R�Ȕ�ړx�l�������ړx��͌��ʂɗp����D
�����ړx�Ə��ʕt���ړx�̈Ⴂ
���ʂ̂���J�e�S���[�ɕ]���Ώۂނ���ꍇ�������ړx�l�ƌĂԂ��Ƃɂ���D�T�i�K�]��ړx��i�t���]���Ȃǂ͂��̗�ł���D����C�]���Ώۂ��P�ʁC��Q�ʂƂ����悤�ɏ��ʕt����ꍇ�����ʕt���ړx�ƌĂԂ��Ƃɂ���D��{�I�ɗ��҂͑召�W�݂̂����ɂȂ�̂ŁC�f�[�^�Ɋ܂܂�Ă�����͓����悤�Ɋ����邪�C���ۂ̉��p�I��ʂɂ����ẮC���炩�ɈقȂ�����܂܂�Ă���C�Ӗ����Ⴄ�D�����ړx�̏ꍇ�́C�Ώۂ̉��p�I�ȃE�F�C�g�i�����x�Ȃǁj�́C���ׂē������C�ړx�l�������ɂȂ��Ă���D���ʕt���ړx�́C���p�I�ȃE�F�C�g���̂��̂�\���������̂ł���C�ړx�l�̓E�F�C�g�i�����x�Ȃǁj���̂��̂�\�����Ă���D
�@���������āC�����ړx�ɂ́C�ݐσ��W�X�e�B�b�N���Ȃǂ̓K�p��c���@�̗ݐϏ������\�ł��邪�C���ʕt���ړx�ɂ́C��ʂ݂̂��d�v�ł���̂ŁC�Ώ̌^���z�̗ݐϓI�����͕s�K���ł���C�w�����z�Ȑ��̂悤�Ȋ��`���K���Ă���D�w���s���Ȃǂ́C��ʂ݂̂��d�v�ł���̂ŁC���ʂ��d�����Ȃ��悤�Ȏړx�ɕϊ����邱�Ƃ��d�v�ł���D�R���W���C���g����̏����t���f�[�^�Ȃǂł́C�Ώ̌^�̕��z��p��������C���ʂ����̂܂ܓ��_�����邱�Ƃ̕����\�������܂��s���D����ɁC�펯�I�ɍs���Ă���悤�ɁC��P�ʂɑ傫�ȃE�F�C�g��u���ϊ����K�v�ł���D���Ђł́C�����t���f�[�^�ɂ��ẮC�@�����l�Ɏw�����z�Ȑ��𗘗p�����m�����g���b�N�v�����͂�p������C�A���ʂ̕]���Ώۂ������t�����Ȃ����@�i�����ʈ����ɂ���j��p�����肵�āC�\���̐��x�����߂�悤�ɂ��Ă���D
�������� adaptation level
�����I�ɑz�肳��锻�f�̊�_�D���鏤�i�̉��i���u�����v�Ɣ��肵���Ƃ��C���̊�̂Ȃ���Δ��f�ł��邪�C����҂̈Ӗ����炷��ƁC���i�̏�Ԃ���\�z����鏇���ȉ��i����_�ɂ��āu�����v�Ɣ��肵���ƍl����D���̊�_�����������Ƃ����D
���ʊ�`�h�b Akaike's infomation criterion
AIC=-2�~�i�ő�ΐ��ޓx�j�{2�~�i���m�p�����[�^�̐��j�D���f�����̓K���x�̊�Ƃ��ėp������D���l���̂́C�������Ă��Ȃ��̂ŁC�����̃��f���̓��Ă͂܂�̗ǂ��̔�r�ɗp�����邱�Ƃ������D�Q��덷��d���W���C���֔�Ȃǂ����f���̓K���x�ɗp�����邪�C�����́C����ړx�̍��ق����̒�`����Ă���D���p��́C��cm�̌덷�Ƃ��C���̂���C�Ƃ����悤�ɑ��肳�ꂽ�P�ʂɂ���ė\���덷��K���x��\������K�v���łĂ���D�������C����ړx�����ς̍��E�ŕs�ρi�P�ʂ������j�Ƃ����悤�ȕۏ��Ȃ��������D�܂��C���f�������G�̂Ȃ�ƁC�قȂ����P�ʂ̑���l���C���f�����Ɋ܂܂�邱�Ƃ����ʂł���D���������āC�K���x�𑪒�ړx�l�̈Ⴂ�ɂ���Ē�`���邱�Ƃ��ł��Ȃ����ƂɂȂ�D
�@�{���C���f���̖ނ��炵���́C�m���I�ȋN����₷���Ȃǂɂ���ăC���[�W����Ă���̂ł��邩��C���̈Ӗ��ŁC����ړx�Ƃ͕ʂ̂��̂ł���D�ނ��炵���𐳊m�ɕ\�����邽�߂ɂ́C�N����Ղ��̊m���I�\���i�m�����z�C�덷���z�ȁj���K�v�ɂȂ�D���ۂ̐��N�m���́C����ړx�Ƃ͌����I�ɖ��W�Ȃ̂ŁC�A���ϐ��ł����U�ϐ��ł��\�킸�C�e�l�ɑ��鐶�N�m������`�����悢�D�ޓx�͂��̂悤�ȋN����Ղ������Ƃɒ�`�����D�Q��덷�Ȃǂ�����C�����̑傫���Œ�`�����Ƃ�����C�ޓx�́C�c���̑傫���Œ�`�����̂ŁC�����ړx�͎g��Ȃ��D
�@���ʊ�`�h�b�́C���f���̓K���x���C�ނ��炵���ɂ���Ē�`�����̂ŁC�m�����z�i�����ɁC�ꐔ���Œ肵�Ȃ����K���z�Ȃǂ̎w�����z�����g����j�����܂�C���`���f�����܂ލL���K�p���邱�Ƃ��ł���D�������C���p��́C�\���l���Ƃ̌ʂ̒P�ʂ̍���p���Ȃ���C�Ӗ�������Ȃ����Ƃ������̂ŁC�ߎ��I�ł����Ă������I�ɕ����Đ��`�I�ȕ\����p����Ȃ���Ȃ�Ȃ��Ȃ�D
�V���i�̃V�F�A�\�����u�V�F�A�\���v�Q�ƁD
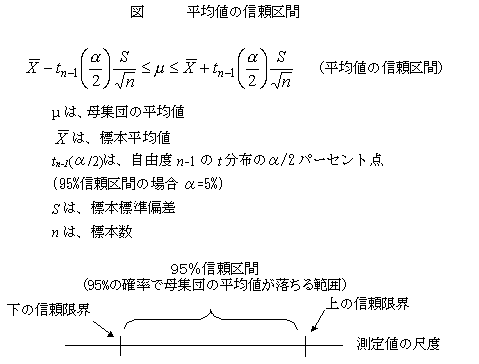
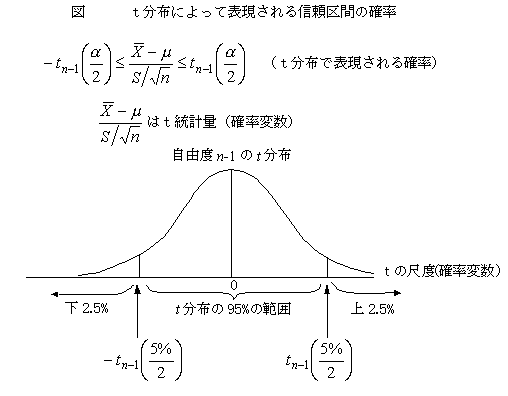
�M����� confidence interval�A�M�����E�A��Ԑ���A�M���x�i���ϒl�ɂ��āj
�@�M���xconfidence level95%�̐M����Ԃ́A��W�c�̕��ϒl��95%�̊m���ŗ�����ƍl������͈͂��Ӗ�����B�v�Z���́A���̂悤�ɂȂ�B99%�̐M����Ԃ́A95%�����m���Ȕ͈͂ł��邩��A�͈͂͂��L���Ȃ�B
�@�W�{���ϒl�̕��z�́A�ꐔ�̕W���������܂��Ă��Ȃ��̂ŁA�m���ϓ�����W�{����W�����𐄒肷�邱�ƂɂȂ�A���K���z�����镽�ϒl�ƃJ�C�Q�敪�z������W�����i�Q��a�j�̔�ł���t���z�ɂ���Ē�`�����i�W�������m���ϓ����Ȃ��ꍇ�ɂ͐��K���z�ɂ���Ē�`�����j�B���������āA�M�����E�́At���v�ʁi�m���ϐ��j�̎ړx��Œ�`����At���瑪��l�ړx�֕ϊ����邱�Ƃɂ���āA�M����Ԃ����߂���B�i����t���z�̎���ό`����ƁA�M����Ԃ̎������߂���B�j95%�̐M����Ԃ̏ꍇ�A�㉺��2.5%���͈̔͂�����̂ŁA�����z��2.5%�_���g����B���W����䗦�i�p�[�Z���g�l�j�Ȃǂ̐M����Ԃ́A���l�ɏ���≺��������̂ŁA�M����Ԃ́A�_����l�ɂ��č��E�Ώ̂ɂȂ�Ȃ��̂����ʂł���B
�S���X�P�[�� psychological scale
�����I�Ȏړx�i������cm��d����g�C���邢�͋��z�Ȃǁj�ɑ��āC�l�Ԃ̍s���ɒ��ڊW����ړx�l��S���X�P�[���Ƃ����D�S���X�P�[���͒��ڊώ@�ł��Ȃ������\���̂ł��邪�C���̑傫�����G�l���M�[�ʂ����f�V�x���l�̋߂����ƂȂǁC����������K�Ȃ���Ȃ���肵���ړx�ł���ƌ�����D
�S���ړx�\���@ psychological scaling
�l�Ԃ̊��o�ʂ𑪒肷��ړx�������@�D�����́C�h���������ʂƂ��đ��肳��Ă���̂Łi���邳��d���Ȃǁj�C�����ʂƐS���ʂƂ̊��W����舵�����Ƃ��������C�Ή����镨���ʂ�����ł��Ȃ��S���ʂ̏ꍇ������D���̏ꍇ�C�ړx�\����������Ŏ����̈Ӗ������m�ɂȂ邱�Ƃ������̂ŁC���q���͂Ȃǂ̑��ϗʉ�͂Ɠ����悤�ȖړI�ŗ��p�����D�m�\�ړx�ł́C�N���A�[�����ۑ�̓���̓x������߂���C�C���[�W�ړx�̏ꍇ�ɂ͓��ꎟ���Ƃ��Ĉ����鍀�ڌQ���߂��ƂȂǂ��ړx�\���ɂȂ�D
�S������@�i���_����@�jpsychometrics
�����ɐl�Ԃ̐S���ʁi�������ʁj�𑪒肷����@�D�L���Ӗ��ōl����C���ʓI�Ȕ����݂̂Ȃ炸�C�����C���ށC���邢�͌���Ȃǂ�����ɓ�����̂ŁC�q�ϓI�Ɏ��W���ꂽ�f�[�^�͂��ׂĐS������ƌ����邱�ƂɂȂ�̂ŁC�p�ꎩ�̂̌����Ȓ�`�͂��܂�d�v�ł͂Ȃ��Ȃ�D�����I�ɓ����ł����Ă��C�l�Ԃ������������ʂ��قȂ��Ă���ΈقȂ����s�����N����Ǝv����̂ŁC�h���Ƃ͈قȂ����ړx�����邱�Ƃ�O��ɂ��Ă���D�s����\������ꍇ�ɂ́C�����h���ł͑Ή��ł��Ȃ��Ƃ��ɂ͐S���I�ȍ\����z�肷�邱�ƂɂȂ�D
�S���I���_(�[���_)
�]��ړx���Δ�r�@�Ȃǂǂ�ȏꍇ�ł��C�l�Ԃ������Ă�����e���C���f�ړx�ɕ\������Ƃ��ɂ́C���f�ړx�̌��_��z�肵�Ă��邱�ƂɂȂ�D��������C���f�Ƃ́C���_��z�肷�邱�ƂƎړx�l�����߂邱�Ƃ��Ӗ�����D��Δ�r�Ȃǂ̂悤�Ɍ��_�ɂȂ�h����팱�҂ɒ���ꍇ�͖��m�ł��邪�C��Δ��f�̂悤�ɁC��r���ׂ��h��������Ȃ��ꍇ�ł́C�S���I���_�́C����I�Ȑ���������n��ɂ���č\������邱�ƂɂȂ�D��̐H�i��H�ׂĂ���������]������Ƃ��C�u���������v�Ƃ������Ƃ��ɂ́C���̔팱�҂ɂƂ��āC���������̒����_�Ƃ̑Δ�ɂ���ĕ]�����Ȃ���邱�ƂɂȂ�D���̒����_���C�ǂ̂悤�ɕ��z���Ă���̂��C�Ƃ��C�ǂ̂悤�Ɍ`�������̂��C�Ƃ����悤�Ȗ��́C���i�J���̂��߂ɏd�v�ł���C�s���̃��J�j�Y���̉𖾂ɂ��d�v�Ȗ��ƌ�����D���������Q�ƁD
�S����������@ psychophysical measurement
����̎h���i���Ⓑ���Ȃǁj�Ɠ����傫���̎h���𑽐��̎h���̒�����T���Ƃ��C�����ɂ���Č��̎h���Ɠ������̂��I��Ȃ��i���̍��o�j�D�܂��C�����I�Ȏh���̊��o��S���I�Ȋ��o�ɒu��������ƁC�����I�ȗʂ����̂܂܍Č������Ƃ͌��炸�C�n���I�Ȋ��W�����o�����D����h���i�W���h���j�Ɠ����Ɗ�����傫���𑪒肷����@�Ƃ��āC��\�I�ȕ��@�Ƃ��čP��@�C�ɏ��ω��@�C�����@�Ȃǂ͂���D�Q�̎h���̔䗦�肷����@�ɂ͔{�����f�C�䗦���f�Ȃǂ�����D
���l�I�v�Z�ɂ�鐄��@
�Ⴆ�C�ő�l��ŏ��l�����߂�Ƃ���A���������������ꍇ�ȂǁC���f�������牉�Z�≼��ɂ���ĉ�͓I�ɋ��߂��Ȃ��ꍇ������D���̏ꍇ�C��̓I�Ȑ��l���^����ꂽ�Ƃ��ɁC���߂�l���v�Z����葱�����Ӗ�����D�ł��P���ȕ��@�́C���p��K�v�Ȑ��x�i�����ݕ��j�ŁC�\�Ȃ��ׂĂ̏ꍇ���v�Z���āC�ړI�ϐ��̒l���r���邱�Ƃł���i������@�j�D���̕��@���n���I�ɍs���R�o��@�C�����e�J�����@�Ȃǂ�����D��͓I�ɉ����Ȃ��ɂ��Ă��C�ړI�ϐ��̓�����������x�����Ă���ꍇ�i�A�����Ă���Ƃ������\�C���Ƃ̊��̌`�������Ă���Ƃ��j�́C����͓I�ȗv�f�̂���j���[�g���@�i���ϐ��̏ꍇ�̓j���[�g���E���t�\���@�j��ŋ}�~���@�Ȃǂ�����D�j���[�g���@��ŋ}�~���@�Ȃǂ́C�����l����o�����āC�ړI�ϐ����œK�ɂ�����������߂āi���z�̒Ⴂ�������邢�͍��������C�����W���̒l�j�C�œK�l�����߂�D�ړI�ϐ��̒l���̂���͓I�ɋK�肵�Ȃ��ŁC���̓s�x�œK�l���v�Z���邱�ƂƁC���m�������߂�葱�������݂Ɍv�Z����d�l�A���S���Y���Ȃǂ�����D�����鐄��l�́C�T�O�I�ɂ͋ߎ����ł��邪�C�덷����������Ύ��p��C���̌v�Z���x�ɂ́C�قƂ�ǖ��Ȃ��D���_�́C��͓I�ɋ��߂��Ȃ��̂ł��邩��C�K�������ŏ��l��ő�l�ɂȂ�ۏ��Ȃ����Ƃł���C�قȂ�������≼�肩��C�ۏ�^���邱�ƂɂȂ�D�Ŗޖ@�̏ꍇ�ɂ́C�w�����z���Ƃ��Ă̓�����p����C���l�I�ɋ��߂��邱�Ƃ��ۏ����D�R���s���[�^��p���邱�Ƃ�O��ɂ��āC���p���̗v���ɓ�������@�ł���D��͓I�ɋ��߂�����𐔒l�v�Z�@�ŋ��߂邱�Ƃ��ł���D
�������f��
���w�I���f���Ƃ������D�l�Ԃ̍s���Ɉ�ʓI�Ȑ��w�I�Ȋ��Ă͂߂���C�s���̃v���Z�X���{�v�f�ɐ��w�I�Ȍ����Ă͂߂��肵�āC��㈂␄�_�ɂ���Č��ۂ�\�����邱�Ƃ��悭�s����D��{�v�f�ƋK���̃��x���Ő��w�I�ȃ��f�����K�p�ł���Ȃ�C�\�����ɂ߂ăX���[�Y�ɂł��邱�Ƃ͂��Ȃ�L���Ȃ��Ƃł���D��ʓI�ɁC�P���Ȓ����̑����Z�C�����Z�̂悤�Ȑ��w�I�K���́C�����ɂ͎��ۂ̌��ۂɓ��Ă͂܂邱�Ƃ͂Ȃ��C��̐������f���Ƃ��Ď�舵�����ƂɂȂ邪�C�قƂ�ǂ̏ꍇ�C�덷���ł�����x�ɐ��x���グ�邱�Ƃɂ���āC���w�I�K�����g�����Ƃ��ł���D
���ʉ��P��
����̐��i�̍w���ӌ��Ȃǂ̖ړI�ϐ��i�O�I��Ƃ������j�ɂ��āC���Z�n��C���ʁC���l�ύ��ڂȂǕ����̍��ڂ���\���������Ƃ��C���ʉ��P�ނɂ���ė\��������邱�Ƃ��ł���D�d��A���͂������悤�ȗ\���������Ƃ��ɗp�����邪�C���ʉ��P�ނ́C�\���ϐ������ʂ⋏�Z�n�ȂǃJ�e�S���[�ŕ\����鎿�⍀�ڂɂȂ��Ă��邱�Ƃ������ł���D���������āC�J�e�S���[�f�[�^�̏d��A���͂ƌ�����D��@�́C�J�e�S���[���O�P�f�[�^�ɒ����C�����N������h������������C�ŏ��Q��@�ʼn�����̂ŁC�d��A���͂̈�ƌ�����D���ʉ����͂ƌ����Ƃ��ɂ́C�ϐ����J�e�S���[�ŕ\�����ꍇ�̕��͖@�ł���D���ʉ��P�ނ̉�͖@�́C���U���͂Ƃ��Ēm��ꂽ���͕��@�̓���ȏꍇ�i���ݍ�p�����肵�Ȃ����Ɓj�Ƃ�������D
���ʉ��R��
���ʉ��R�ނ́C�ϐ����J�e�S���[�ł���ꍇ�ɁC�J�e�S���[�Ɖҁi�����T���v���j����ԓI�Ƀv���b�g���邽�߂ɗp������D���q���͂��C�P�ʂ̈قȂ鐔�ʁi�g���Ƒ̏d�Ȃǁj�f�[�^�̂Ƃ��ɁC�ϐ��ƒ����T���v������ԓI�Ƀv���b�g���邽�߂ɗp������̂Ǝ��Ă���D���ʉ��R�ނ̕��͌��ʂ́C���̉�]�����Ȃ��̂���ʓI�Ȃ̂ŁC���q���͂����ނ���听�����͂ɋ߂��D���ʉ��R�ނ́C���ڂƉ҂ꎟ���ɂ̂��āC�����J�e�S���[�Ƃ��̃J�e�S���[�ɉ����l���߂��Ɉʒu�t������@�ł���ƌ�����D���������āC�������\���ł���Ȃ�C�҂̋߂��ɂ���J�e�S���[�́C���������C���̐l���Y�����Ă���ƌ�����D�������C�f�[�^�����̂܂ܕ��͂���ƁC�S�̂Ƃ��ĊY���Ґ��������J�e�S���[�����ʂɑ傫�ȉe���͂������Ă��܂��̂ŁC�Y���x���̑召��������C���d���ڂ�����ꍇ�ɂ́C���̑��������ʂɉe������̂ŁC�ґ��̉��ɂ��Ă��������ĕ��͂���D���ʉ��R�ނ́C�听�����͂ȂǂƓ��l�C�����̎����ɂ���ċߎ��ł��Ȃ��ꍇ�ɂ́C���̎����Ő����ł��Ȃ��J�e�S���[��T���v���͒����ɕz�u�����̂ŁC�f�[�^�ɂ�����ގ��W�Ɩ��������z�u�ɂȂ邱�Ƃ�����D���ʉ��R�ނ́C�听�����͂Ɠ��l�ɁC�����̂��̂̈Ӗ������p�ɓK���Ȃ��ꍇ������̂ŁC�����������Ȃ��ċ�ԓI�ɔc���ł��Ȃ��Ƃ��ɂ́C�����ɈӖ������邩�Ȃ����̉��߂�����Ȃ�D
���ʉ��R�ށE�R���X�|���f���X���́E�o�Ύړx�@
�R�̕��@�́C��舵���f�[�^���K���I�ɈقȂ��Ă���̂ŁC�f�[�^�̌`����������@���قȂ��Ă��邪�C���̌�̉�͖@�͓����ł���D���̉�͖@�͎听�����͂Ƃ������ł���C�ŗL�l�E�ŗL�x�N�g�������߂邱�ƁC���ْl�����C�G�b�J�[�g�E�����O�����ȂǂƂ���v����D
�@�R���X�|���f���X���͂́C�W�v�\�����͂̑ΏۂɂȂ邱�Ƃ������̂ŁC�}�C�i�X�̂Ȃ��|�A�\�����z�C���z�C�������z�C�����z�Ȃǂ̊��Ғl�i���ϒl�j�ƕ��U�ɂ���Ċ������D���ʉ��R�ނ������ł��邪�C�R���X�|���f���X���͂́u�W�v���ڂ̍s�v�f�v�Ɓu��v�f(���ځj�v��Ή�������i���ւ��ő�ɂ���j�D���ʉ��R�ނ́C�s�v�f���l�T���v���ł���̂ŁC�u�l�v�Ɓu�J�e�S���[�v��Ή���������@�ł���D���ʉ��R�ނŁC���N��Ȃǂ̏W�v�����ƍ��ڂ�Ή�������Ƃ��ɂ́C�l�̃T���v���X�R�A�𐫔N��ʂɕ��ς��ăv���b�g���邱�ƂɂȂ�̂ŁC���N��Ȃǂ̑����ԂɈႢ�������l���v�����傫���Ƃ��C�����͒����Ɍł܂��ĕz�u�����D���N��Ȃǂ����ڂƑΉ����������Ƃ��ɂ́C�W�v�������ʂ��R���X�|���f���X���͂���C���܂��Ή������邱�Ƃ��ł���D�������C���Ƃ��ƁC�l���ɍ��E����鍀�ڂ̏ꍇ�C�R���X�|���f���X���͂ł́C�����ȕ��U��������Ė������ɑΉ������Ă���\��������̂ŁC���ӂ��Ȃ��ĂȂ�Ȃ��D������ɂ��Ă��C�R���X�|���f���X���͂́C���ڂƏW�v�������ϓ��ɑΉ���������@�i���ւ��ő�ɂ�����@�j�Ȃ̂ŁC���߂��₷�����ʂɂȂ邱�Ƃ������D�O�P�f�[�^�ɂ��̂܂܃R���X�|���f���X���͂�K�p�����̂����ʉ��R�ނł���C�t�ɁC�x���̐��ʉ��R�ޕ��͈͂�ʓI�ȃR���X�|���f���X���͂ɂȂ�D�o�Ύړx�@�́C���m�̓��_�̋��ԕ��U�̍ő剻�Ƃ�����Ő��������̂ł��邪�C�������@�ɂȂ�D�����̎d���̈Ⴂ�Ō����C�u�s�Ɨ�̂Q�d����f�[�^�̎听�����́v�u����f�[�^�̃p�^�[���ގ��x���́v�u����f�[�^�̓W�J�@���f���v�ȂǂƂ�������D

���ʉ��R�ނƐ��݃N���X���͂Ƃ̈Ⴂ
�@�Ƃ��ɃJ�e�S���[�ϐ��̕��͖@�ƌ����Ă��邪�A��{�I�ȍl�����͈قȂ��Ă���A�ړI�ɂ���Ďg��������K�v������B
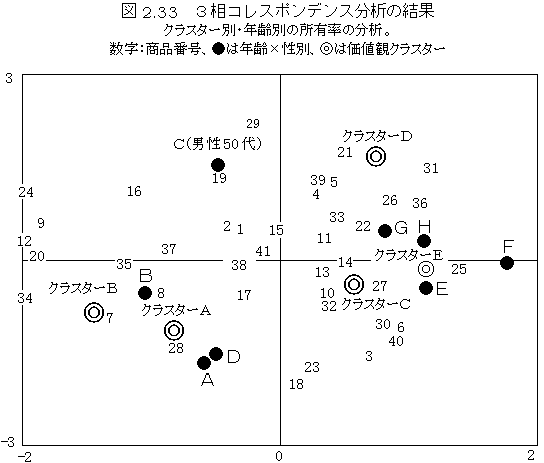
�@���ʉ��R�ނ́A���̑��֕��͂ł���A���ڂƕ]���҂̊֘A�x�s��i�����f�[�^���̂��́j����A�݂��ɑ��ւ��鍀�ڃJ�e�S���[����Ǝ��̎��������߂�B�����̏ꍇ�A�Ǝ��̕����̎����́A���̕��U�i�ŗL�l�j�̑傫�����ϓ��ɂ������_�i�T���v���X�R�A�j�̑召�W��������A�ގ��W�͂����肷��B���֊W����ϓ��ȓƎ��̎��������߂�̂ł��邩��A���ϗʉ�͂̓����������Ă���B
�@���݃N���X���͂́A�d��A���͂̓Ɨ��ϐ��̂悤�ɁA�{���I�ȕϐ��Ԃ̑��֊W��z�肵�Ȃ��̂ŁA��{�I�ɑ��ϗʉ�̖͂ړI�Ƃ͈قȂ��Ă���i�u���ϗʉ�͂̒�`�v�̍��ڂ�u�f�[�^���͓���Q�v�Ȃǂɑ��ϗʉ�͂̍l����������j�B�d��A���͂̏ꍇ�́A�Ɨ��ϐ��Ԃ̖{���I�ȑ��ւ�z�肵�Ȃ����A��������̑��ւ���菜���āA�v�����ʂ͂���B���݃N���X���͂ł́A�ϐ��Ԃ̑��֊W��z�肵�Ȃ������łȂ��A����ꂽ�f�[�^�̋��ϓ������́A�����ɏo�������f�[�^�̑傫����\�����Ă���ƍl����B�Ɨ��������q���_�́{�{�A�{�|�A�|�{�A�\�\�̏o���x���̂悤�Ȃ��̂ł���B
�@���������āA���݃N���X���͂ł́A�ŗL�l�����߂�Ƃ��A�f�[�^�̐Ϙa�s��i�{�����[����\���f�[�^�j�̂悤�ȓx���̑傫�������̂܂ܔ��f�����f�[�^�͂��邱�ƂɂȂ�B�Ϙa�n�̃f�[�^�́A�Q�d�N���X�A�R�d�N���X�ȂǍ����̃N���X�f�[�^�ɒP���W�v�̂悤�ȍ��ڂ̏o���x���̑傫�������f�����̂ŁA�����̃N���X�\�͂���A�f�[�^�̑S�̂̌X����c���ł���i�R���X�|���f���X���́A�J�C�Q�挟��A���U���͂Ȃǂ́A����ʂ���ݍ�p�����邪�A���݃N���X���͕͂������Ȃ��j�B
�@���̂悤�ɂ��ē�������݃N���X���͂̎����i�ŗL�l�j�́A�x���f�[�^�̑傫�����ł��傫���������鎟��������������̂ŁA�҂̉x����������鎟���ł���A���݃N���X�����̑傫�����ɕ\�����Ă���B
�@���݃N���X���͂́A���ʉ��R�ނ̂悤�ɕ����̍��ڂ���Ɨ��������������߂�Ƃ������@�ł͂Ȃ��A�x���̑傫���Ƃ�������ԂɌ����o�����@�ł���B���������āA���ڊԂɖ{���I�ɑ��֊W������ꍇ�ɂ́A���݃N���X�����߂�Ƃ��A�������ڂ����x���g���Đ��݃N���X�����߂�悤�Ȃ��ƂɂȂ��Ă���̂ŁA�L���Ȑ��݃N���X�������Ă��Ȃ����ƂɂȂ�B���ڊԂɖ{���I�ȑ��֊W������ꍇ�ɂ́A��U���q���͂␔�ʉ��R�ނɂ���ēƗ��������������߂āA�O�P�p�^�[�������A���̃f�[�^����݃N���X���͂���Ɨǂ��N���X�������邱�Ƃ��\�z�����B���̏ꍇ�A�Ɨ��������_�̃N���X�^�[���͂��ȗ��������ꍇ�ɂȂ��Ă���ƌ�����B
���ʉ��Q��
�@�\���ϐ����J�e�S���[�ϐ��̂Ƃ��C�����Q�̗\�������\��������@�����ʉ��Q�ނɂȂ�D�J�e�S���[�ϐ��̔��ʕ��͂ƌ����Ă���D�J�e�S���[�ϐ�����舵���Ƃ��ɂ́C�J�e�S���[���O�P�^�̕ϐ��ɕϊ����C��̃J�e�S���[���O�Ƃ��ăJ�e�S���[�E�F�C�g���v�Z����D���ϗʉ�͂̏d���ʕ��͂ɂ�����D
�@���ʉ��Q�ނɂ��Ă̏ڂ������e�́A�������u�R���X�|���f���X���̗͂��p�@�v�A�u���ϗʉ�A���́E�������֕��́E���ϗʕ��U���́v�A�u�f�[�^���͓���Q���ϗʉ�͖@�E�l�c�r�̉��p�v�ȂǎQ�ƁB
�X�`�[���E�h���X�̑��d��r
�m���p�����g���b�N�ȑ��d��r����@�D���ϒl�̑��d��r�@�ł���`���[�L�[�E�N���[�}�[�@�i���ϒl�v�Z�̂m�����������Ȃ��Ƃ��ɒ��a���ς�p����ꍇ�̃`���[�L�[�@�j�ɂ����ĕ��ϒl�����ʂɒu�������đΔ�r����D���茋�ʂ́C�ʏ�̃e���[�L�[�@�Ɠ��l�ɃX�`���[�f���g�����ꂽ�͈͂̕\��p����D
�X�e�b�v���C�Y�@ step-wise method
�d��A���͂┻�ʕ��͂Ȃǂ̂Ƃ��Ɏg����ϐ���I�ԕ��@�D�Ɨ��ϐ��Ԃ̑��ւ������Ƃ��i���d�������j�C�f�[�^�̏����ȕ�ɂ���Đ���l���傫���ω�����悤�ɁC����l���s����ɂȂ����肷��D�܂��C����l�͓Ɨ��ϐ��̓Ǝ��̊�^���\�������̂ŁC�݂��ɑ��ւ̍����Ɨ��ϐ��͌X�̊�^�͍����̂ɗ��������ɕ��͂���Ɨ����Ƃ���^�����Ⴂ�悤�Ɍ�����ȂǁC���߂����Â炢���ʂɂȂ邱�Ƃ������D���̏ꍇ�C�݂��ɑ��ւ̍����ϐ��Q�̑�\���c���C���̕ϐ����������@���X�e�b�v���C�Y�@�ł���D�]���ϐ��ɑ��āC�����Ƃ���^�̍����ϐ����珇�ɕϐ���I�����Ă����C�c��̂ǂ̕ϐ������v�I�Ɍ��ʂ��Ȃ��Ɣ��f���ꂽ�Ƃ��ɕϐ��I����ł�����D�ϐ�����荞��ł����ƁC�����̕ϐ��̊W����C���Ɏ�荞�ϐ��̗L�Ӑ��������邱�Ƃ�����̂ŁC�V�����ϐ�����荞��C���Ɏ�荞�ϐ��̗L�Ӑ��������������肵�ėL�Ӑ���������艺�������Ƃ��ɂ͏��O����C�Ƃ����菇���܂�ł���D����L�ӂȕϐ�����荞��ł����O�i�I�ȑI��@�ɑ��āC�\�ȕϐ������ׂėp�������͌��ʂ���C�����Ƃ��L�Ӑ��̒Ⴂ�ϐ�����������Ă�����ޓI���@������D��ʂɁC��ޖ@�̕����O�i�@���������̕ϐ����c���X�������邪�C�����̏ꍇ�C�قƂ�Ǔ������ʂɂȂ�D�����́C������̂��l�i�e�l�j��p���邱�Ƃ����邪�C�L�Ӑ��̊m���i�T�����P���j��p���邱�Ƃ������D
�X�g���X�w���i�X�g���X�̎����j
���Ђ̃X�g���X�]�����ڂ́C�����ɏA�Ǝ҂ɂ��āC�S���I�ȕs���C��J�C�s�K���Ȃ�10�̃X�P�[���ɂ���Čl��]������D�W�c�肷�邱�Ƃ��ł���D��U�O���ڂ̎���ɑ���Yes�CNo�̉��ʂ���v�Z����D10�̃X�g���X�����ɂ́C�S���I�ȏƐg�̓I�ȏǏ܂܂�Ă���D�C���C�����C���C�͊��C�d���̕s�����C���X���C�ߘJ�X���C�S���I��J�X���C�ݒ���Q�C�s���X���C������J�X���C���M�r�����̂P�O�ړx�D1990�N�O���ɁC����̃I�t�B�X�A�Ǝ�50�`300�l�̎�s�������f�[�^�̈��q���͂ɂ����10�ړx���\������Ă���D
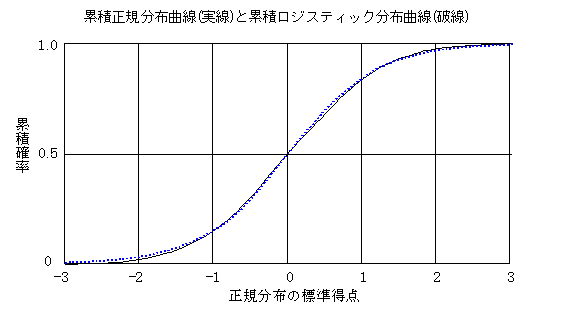
���K���z�Ȑ��ƃ��W�X�e�B�b�N���z�Ȑ�(���W�X�e�B�b�N���j
��ʉ����`���f���Ȃǂɂ����āC�A�����Ƃ��Đ��K���z��z�肵�Ă̔䗦�ϊ��i�v���r�b�g���f���j��W�X�e�B�b�N���z��z�肵�Ă̔䗦�ϊ��i���W�b�g���f���j�Ȃǂ�����D���̂ق��C���W�X�e�B�b�N���́C�v�Z���ȒP�Ȃ��߂ɁC���K���z�̑���ɗp�����邱�Ƃ�����D���K���z�́C�덷���z�Ƃ��ČÂ�����p�����Ă��邪�C�ΐ��ϊ��̍��Ƃ��ĕ\���ł��郍�W�b�g�́C���̃��f�����̂Ƃ��Ă��ϋɓI�ȈӋ`�������ł���D�ݐϕ��z���Ƃ��ė�������ƁC�قƂ�Ǔ����悤�Ȍ`�����Ă��邪�C���̕����̐��p�[�Z���g���x�̊m�����v�Z����ƈႢ���ڗ����Ă���D�}�ł͉����̓��W�X�e�B�b�N����1.7�{���ėݐϐ��K���z�Ȑ��ɍ��킹�Ă���D
���i�i�p�[�\�i���e�B�[�j�̑���
���Ђ̕]�����ڂ́C1980�N��㔼�ɓ��Ў����p�ɁC��r�I�ω����ɂ����s���X���𑪒肷�邽�߂ɍ��ꂽ�D��s���̑�w���i�P�O�Z500�l�j�C�A�ƎҁC��ʏ���ҁi1000�l���x�j�̃f�[�^�����ƂɂT�ړx���\�������D2000�N�̊w�������ɂ��ƁC���t�̈Ӗ����̂��傫���ω����Ă��邱�Ƃ��\�z����āC�s���X���̕ω��Ȃ̂����t�̎g�����̕ω��Ȃ̂���ʂł��Ȃ��Ƃ����悤�Ȍ��ʂ��o�Ă���D
�������֕��� canonical correlation analysis
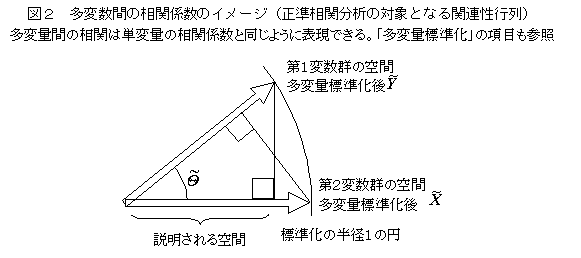
�@��ʂɁA�������֕��͂́A�Q�Q�̕ϐ�����A���W�����ł��傫���Ȃ�悤�ȍ����ϗʂ��\������A�Ƃ������@�ł��邪�A���̕��@�́A���ۂ̗��p��ʂł́A�@���ʊW�̈��q�i�听���j�����߂邱�ƁA�A��P�Q�̃T���v�����_�Ƒ�Q�Q�̃T���v�����_��Ή������邱�Ɓi���d���ʂ␔�ʉ��Q�ނ̌Q�ƃT���v�����_�̑Ή��W�̗�j�Ƃ����Ӗ��������Ă���B�A�̑Ή��W�́A���d���ʕ��͂␔�ʉ��Q�ނ̂悤�ɕЕ����Q�ł���ꍇ�ɂ́A���ʕ��͂Ƃ������m�ȕ��͖@�ɂȂ邪�A�����Ƃ��ϐ��̏ꍇ�ɂ́A����̐��x��\�킷�̂ŁA���p�ɂ͎g���ɂ����B�����ŁA�ϐ��̑Ή��W�i�������_��\���x�N�g�������q���חʁj�����邱�ƁA�������_�𑼂̕��ލ��ڕʁi���ʤ�N��ʂȂǁj�Ɍ��邱�ƁA�Ȃǂɂ���ĉ��p�I�ȉ��l�������B
�@�}�Q�́A�Q�̕ϐ��Q�Ԃ̑��W����\�킵�A���ꂼ��̕ϐ��Q�͑��ϗʂ̕W�������Ȃ���Ă���̂ŁA���ϗʂ̒P�ʃx�N�g���ɂȂ��Ă���i�ʏ�̑��W���Ɠ����C���[�W�j�B�}�R�́A���ϗʂ̑��W���ɂ����郦���s��̌`�ɂȂ邱�Ƃ���A���̎����ߎ��i�听�����́A���ْl�����j���s���邱�Ƃ������Ă���i�������֕��͂̂��Ɓj�B�}�S�͐����W���ƍ\���x�N�g���̋��ߕ��������B�i�ڂ����́A�u���ϗʉ�A���́E�������֕��́E���ϗʕ��U���́v2006�N���Q�Ɓj
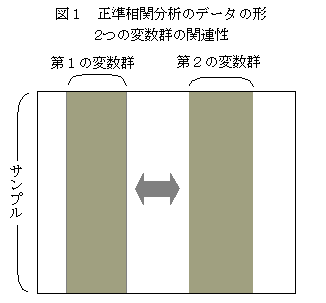

�������֕��́i�R�̕ϐ�������ꍇ�j�����ϗʉ�A���́i�R�̕ϐ��Q������ꍇ�j
�������֕��̗͂��p�@�i�ϐ��Q�̐������E���ʊW�̈��q�ƒP���\���j
�@�������֕��͖@�́A�Ή�����Q�̕ϐ��Q�i�R�ȏ������j�̂��ꂼ��̕ϐ��Q����\������鍇���ϗʁi���d���ϒl�j�̑��ւ��ő�ɂȂ�悤�ɕϐ��̌W���i���d�l�A�E�F�C�g�j�����߂���@�ł��邪�A���p�I�ɂ́A���̂悤�ȈӖ�������B
�i�P�j�قȂ����ϐ��Q���S�̂Ƃ��āA�ǂꂾ���ʂ̕ϐ��Q�ɉe����^���Ă���̂���m�肽���Ƃ��B�Ⴆ�A�I�t�B�X�œ����l�ɂ��āA�����̃X�g���X�ϐ��̌Q�ɑ��āA�I�t�B�X�̊��ϐ��Q�i�Ɩ��A���A�F�ʁA�̗L���A�L���Ȃǁj�S�̂Ƃ��Ẳe���x�A���邢�́A�I�t�B�X�C���[�W���ڂ̉e���x�A�l���v���i�p�[�\�i���e�B�≿�l�ςȂǁj�Ȃǂ̉e���x��m�肽�����ȂǁB���̏ꍇ�A�������W����ݐςQ��a�i����W���j�Ȃǂ��w�W�ɂȂ邪�A����W���́A�Q�Q�Ԃ́u�֘A�x�v��S�̂Ƃ����w�W�Ȃ̂ŁA�Е��̌Q�̕��U�S�̂ɑ���������ł���u�璷���W���v�̑傫�����A�ړI�ɓK�����w�W�ƌ�����B
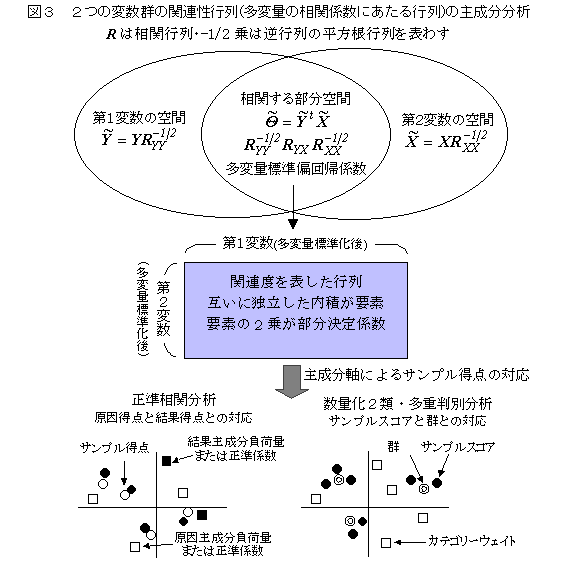
�i�Q�j�������֕��͂́A�Q�Q�Ԃ̊֘A���i���݂̑��W���j�݂̂͂̑ΏۂƂ��Ă���B�֘A����\�킷���W���́A�݂��ɓƗ��ł͂Ȃ��̂ŁA�Ɨ������听���ɗv���B���Ȃ킿�A�֘A����Ɨ��������q�̌`�ő�����B���̐������q�́A���ʊW�̈��q�ł���B���̎���Ō����A���ʂƂ��Ă̊��̃O���[�v���q�ł͂Ȃ��A�܂��A�����Ƃ��Ă̐H���̈��q�ł��Ȃ��B�P�̊����A�����̐H���ƈ��ʊW������i���ւ�������j�A���̕����̐H���͓������q�ɂ܂Ƃ߂��A�܂��A�P�̐H���������ɕ����̊��Ƒ��ւ�������A���̕����̊��Ƃ��̐H���͓������q�Ƃ��Ă܂Ƃ߂���B���̂悤�ɁA�������֕��͂̈��q�i�������q�j�́A�����̑��ւ�����ʊW������q���i�听�����j�����߂���B�ʏ�̎听�����͂Ɠ����悤�ɁA�����̈��q�����o�����ꍇ�A���ʊW�̎听���́A���p���₷�����ʊW�̂܂Ƃ܂��\�����Ă��Ȃ��̂ŁA���͌��ʂ��o���}�b�N�X��]�Ȃǂɂ���āA�P���\�������o����A���Ȃ艞�p���₷�����ʂɂȂ�B
�@�������_�����߂邽�߂̌W���́A�d��A���͂Ɠ��l�ɁA�݂��ɑ��ւ��邱�Ƃ�����q���̉��߂ɂ͎g���Â炢�w�W�ł���B���q���͂̈��q���חʂɓ�����u�\���x�N�g���v��p���Ď��̉��߂�����B����ɁA��]��̍\���x�N�g���i���q���חʁj�͂����Ǝg���₷���w�W�ł���ƌ�����B�i�������q�́A�P�Ȃ�ϐ��̂܂Ƃ܂�ł͂Ȃ��āA���ʊW�̗ގ��x����\�������j
�@���̐}�́A�����\���x�N�g���Ɖ�]��̍\���x�N�g����\�킵�Ă���i���f�[�^�́A�u���ϗʉ�̓n���h�u�b�N�v�̊��̃f�[�^�𗘗p�����Ē����܂����j�B���̐}�ɂ́A���W���s��ɃR���X�|���f���X���͂�K�p�����ꍇ����B�R���X�|���f���X���͂́A�P���ɑΉ������邽�߂ɁA�Ή��W�͖��m�ł��邪�A��]��̍\���x�N�g�����画�f����ƁA�������\��������ƌ�����i��ʂɃR���X�|���f���X���͂́A���̂悤�Ȑ����������Ă���j�B
�������֕��͂̃V�~�����[�V�����\��
�@�������֕��͂́A�d��A�\���Ɠ����悤�ɁA�Ɨ��ϐ��𑀍삷�邱�Ƃɂ���āA�]���ϐ��̈��q���_�i�������_�j��\�����邱�Ƃ��ł���B�d��A���̗͂\���l��1�����ړx����㉺���邪�A�������֕��͂̏ꍇ�A�������q��ԁi���ʊW�̈��q�j��ω����邱�Ƃ������ł���B�������֕��͂́A���`���f���ł���̂ŁA1�̓Ɨ��ϐ��Ԋu�ɕω�������ƁA��ԏ���I�ɓ��Ԋu�ŕω�����i�}�Q�Ɓj�B�i���f�[�^�́A�O���ڂƓ��l�A���䑼�u���ϗʉ�̓n���h�u�b�N�v�Ɍf�ڂ��ꂽ���̂𗘗p�����Ē����܂����B�j

�������� canonical decomposition
�@���ْl�����́A�Q���̌`�̍s����A�s�v�f�̌ŗL�x�N�g���i���W�l�j�E��v�f�̌ŗL�x�N�g���A�ŗL�l�̕������i���ْl�j�ɕ���������@�ł��邪�A���̍l�������R���\�Ɉ�ʉ�����ƁA�R���f�[�^���A�R�̗v�f�̓��_�̊|���Z�ɂ���ĕ\������`���ɂȂ�B�R�̑��́A���������ɂ���ĕ\�������̂ŁA���ْl�����̌��ʂ��s�v�f�A��v�f�������ԓ��̓_�ɂ���ĕ\�������̂Ɠ��l�ɁA�R�̑��̗v�f�͓����ԓ��̓_�Ƃ��ĕ\�������B����́A�R���f�[�^�̎听�����͂Ƃ�������B�Q���f�[�^�̌ŗL�l�Ɠ����悤�ɁA�R���f�[�^�̂��ׂĂ̗v�f�̂Q��a�ƈ�v����悤�Ȑ��l���`�ł��邪�A�����N��Q�̑��̌ŗL�x�N�g���̑g�ݍ��킹�Ȃǂɂ��āA�K���������炩�ɂȂ��Ă���킯�ł͂Ȃ����A�ސ��I�ɓ��ْl��������ʉ��������̂Ƃ��ĉ��p���邱�Ƃ��ł���B�听�����͂̌��ʂ𗘗p����Ƃ��ɂ́A�s�Ɨ�̗v�f�̃E�F�C�g�t����ꂽ���_�̑��ւ��ő�ɂȂ�Ƃ����i�Ή�������j������t�������A�R���X�|���f���X���͂Ƃ��ĕ\����������������Ղ��̂Ɠ��l�ɁA���������̌��ʂ��A�R���R���X�|���f���X���͂Ƃ��āA�R�̑��̗v�f�̑Ή��W��\�����邽�߂ɗp���邱�Ƃ��ł���B���������ɂ��ẮACarroll&Chang,1970��Comon,2004�ȂǎQ�ƁB
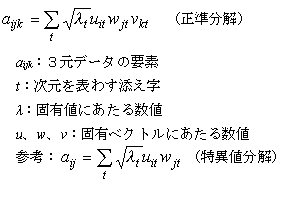
�����Ȑ�
�P�������̌X���������C�l�Ԃ̋@�\�i�w�K�Ȑ��j��W�c�̐����X����\������Ƃ��ɗp������D�s���̋L�q�Ɋւ��ẮC�w�K�Ȑ��i�L�����ʂ̋Ȑ��j�C���W�X�e�B�b�N�Ȑ��Ȃǂ̖O�a���f���i�Q�ߐ������j�C�S���y���c�Ȑ��Ȃǂ����p����Ă���D
�Ϙa�̈��q���͖@
�Ϙa�i���ρj�s���p���Ď听�����͂�������C������]�����邱�ƁD�ʏ�̈��q���͂́C���ς��̕��C���U�ɂ��ړx�P�ʕϊ����s�����f�[�^�ɑ��āC�Ϙa�̕��͂����Ă��邱�Ƃ��Ӗ����Ă���D�Ϙa�̕��͂ł́C���肳�ꂽ���l�����̂܂ܕ��͂ł���悤�ȈӖ��̂���ړx�ɂȂ��Ă��邱�Ƃ��K�v�ł���D�Ϙa�s����听�����͂��邱�Ƃ́C�s��̓��ْl�������邢�̓G�b�J�[�g�E�����O�����ȂǂƌĂ�邱�Ƃ�����C���ύs�烉���N�̒Ⴂ��ԕz�u�ɂ���ċߎ�����Ƃ��̕��@�ł���D�f�[�^���璼�ڐϘa�s������߂�ꍇ�ɂ́C���ϐ�����ړx���䗦�ړx�Ƃ��đz��ł��邱�Ƃ��K�v�ł��邪�C�l�X�ȉ���ɂ��ϊ���ɕ��͂�����@�ɂ́C�听�����͂��͂��߃g�[�K�[�\���̂l�c�r�i����W���́j�C���ʉ��V�ށC�R���X�|���f���X���́C�o�Ύړx�@�C�l�c�o�q�d�e�ȂǂƌĂ�Ă�����@������D
�����ϐ��̉��߂ɂ��Ă̂Q�̌��Ƒ��d������
�@�v�����́i���ɏd��A���͂Ȃǁj�̐����ϐ��̌��ʁi�v�����ʁj�̉��߂ɂ��āA���̂R�̏ꍇ���悭�N����B�����Ȃǂɂ����Ă��鐻�i�̍w���ӌ��ɂ��āA�N��Ɛ��ʂ̌��ʂ��������Ƃ��A�N��Ɛ��ʂƂ͖{���Ɨ������ϐ��Ȃ̂ŁA�N��ʁA���ʂ̒����l���ɕ肪����Ƃ��̑��ւ́A��������̑��ւƌ�����i�����͎�N�҂������j���͔N���҂������ꍇ�Ȃǁj�B���̏ꍇ�A�w���ӌ����A�����������j�����Ⴍ�Ȃ����Ƃ��A�����̕����w���ӌ��������ƌ��_����ƌ�������_�̉\��������B�����̕�����N�҂������̂ŁA���ۂɂ́A�����ł͂Ȃ��N���\�����Ă���\�������邩��ł���i�{���ł̓^�C�v�`�̌��ƌĂ�ł���j�B���̏ꍇ�A���ʕϐ��ƔN��ϐ����̕��͂���i�d��A���́j�ɂ���āA�݂��ɒ������������̗v�����ʁi���ʂ̌X���j�𐄒肷�邱�Ƃ��ł���B
�@�܂��A�����������̂��������ɂ��āA����₩���]���ƃX�b�L�����]��������ϐ��ɂ��ďd��A���͂����Ƃ��A�X�b�L�����̕Ή�A�W�����}�C�i�X�ɂȂ邱�Ƃ�����B�����̏ꍇ�A���������ʂł��邪�A���߂ł��Ȃ��ƌ����ăf�[�^�����������ƍl���邱�Ƃ�����i�{���ł͉��߂ł��Ȃ��ƍl���邱�Ƃ��^�C�v�a�̌��ƌ����Ă���j�B�d��A���͂��݂��ɒ�����������̗v�����ʂ𐄒肷��̂ŁA����₩���ƃX�b�L�����̑��ւ���������̑��ւƂ��āA�������Ă��܂�����A�Ή�A�W��������₩���A�X�b�L�����̌��ʂ�\�����Ă��Ȃ�����N���邱�Ƃł���B�{���I�ɑ��֊W�̂�������ϐ��̌��ʂ́A�P���W���ɕ\������Ă��邱�Ƃ������B
�@�^�C�v�`�̏ꍇ�ɂ́A�����ϐ��͓Ɨ��ϐ��ƌĂׂ邪�A�^�C�v�a�̏ꍇ�́A�Ɨ��ϐ��Ƃ͌������炢�B�Ɨ������ϐ��́A�f�[�^�̑��ւƂ͖��W�ɋ�ԓI�ɒ�������z�肷��B�{���I�ɑ��ւ̂���ϐ��݂͌��ɎΌ��W�ɂ���B�Ɨ��ϐ��̌�������̑��ւ́A��������Ńf�[�^�����ւ������ĕz�u�����B
�@���d�������́A�Ɨ��ϐ��i�������j��ԏ�̃f�[�^���A�ׂ�����ɕ��ꍇ�ł����āA���̂悤�ȃf�[�^���畽�ʂ𐄒肷��i��A�W���̌X���𐄒肷��j�ɂ͕s�K���Ǝv����ꍇ�ł���B�ׂ�����ɕ��f�[�^�̕��ʂ𐄒肷��ꍇ�A�傫�Ȍ덷�����ʂ]������قlje���͂����̂Łi��ԑS�̂Ƀf�[�^�͌덷�̑召�����ʂ]�����邱�Ƃ͂قƂ�ǂȂ��j�A���Ȃ�s����Ȑ���l�ɂȂ��Ă���Ǝv����B���������āA�݂��ɑ��ւ̍����Ɨ��ϐ��̗v�����ʐ���l�͐M���ł��Ȃ��B���Ƃ��Ƒ��֊W���z�肳���ꍇ�̐����ϐ��i��L�̂���₩���ƃX�b�L�����Ȃǁj�̕Ή�A�W�������߂ł��Ȃ��̂́A���d�������Ƃ͌���Ȃ��̂ŁA���͕��@���̂��s�K���ȏꍇ�������i�P���W�����K���ȏꍇ�������j�B�����U�\�����́A�������֕��͂Ȃǂł��A���߂ł��Ȃ��W���́A�^�C�v�a�̃P�[�X�������B
�y���_
�@�y=(x-m)/�Ёim�͕��ρC�Ђ͕W�����j�ŕϊ������l�D�ϊ���͕��ςO�C���U�P�ɂȂ�D�f�[�^�����K���z����Ƃ�����C�y���_�́}�P�̊Ԃ̖�68�����܂܂��D���_�̑��ΓI�Ȉʒu��������₷���D�P�ʂ̈قȂ������_�i�g���Ƒ̏d�Ȃǁj�̑��ΓI�Ȉʒu���r����ꍇ�ɂ͕֗��ł���D���l�́C�y���_����}�C�i�X�Ə����_���o���Ȃ��悤�ɕ\�������ꍇ�ƌ�����D�u�W�����v�Q�ƁD
����(�������������Cabsolute threshould)�E�h��臁i�����������j
���Ō����C�͂��߂ĕ������鉹�̑傫���D�h��臂Ƃ������D���ɍ����C�d���C���̑��̊��o�ɂ��Ē�`�����D���ۂ̑���ł́C�������鉹�ƕ������Ȃ��������m�ɋ�ʂł���킯�łȂ��̂ŁC�����̑��茋�ʂ��瓝�v�I�Ɍ��߂���D����@�ɂ��Ă̐S����������@�⊯�\�����@�ȂǁC���茋�ʂ��M���ł���悤�ɁC���̎葱�����m������Ă���D�傫������臂��h�����Ƃ������Ƃ�����D���̑傫���Ȃǂł͎h�����̑���͂ł��Ȃ��̂Ő���l�ɂȂ�D���p�I�ɂ́C���臂������K���C�s������������͈͂̕����d�v�ɂȂ邱�Ƃ������D
�I�D��Apreference�@regression���O���W�J�@�D
���ݍ\�����́i���݃N���X���́jlatent class analysis ���ʉ��R�ނƂ̈Ⴂ�����ʉ��R�ނƐ��݃N���X���͂Ƃ̈Ⴂ
���ݍ\�����́i���݃N���X���́jlatent class analysis �̈Ӗ��Ƃ��ׂĂ̍��ڂ��Ɉ����v�Z�@
�@���݃N���X���͂́A��ɂO�P�^���ڂɂ��Ă̐��ݓI�ȃN���X�i�҂̌Q�j�����߂���@�ŁA�����̏���҂̐��ݓI�ȌQ���������邱�ƂȂǂ̖ړI�ɗ��p�����B
�@�v�Z�@�̊�{�I�ȍl�����́A���̍ł��傫���Ƃ���ɐ��ݓI�Ȏ����߂邱�Ƃɂ���āA�N���X�����̐����͂̍����Q�i���ݓI�ɗL���ȃN���X�j�����߂���@�ɂȂ��Ă���B���������āA��{�I�ɂ͌ŗL�l�i�������̍������U�j�����߂邱�ƂɂȂ邪�A�ʏ�̎听�����́i���q���́j�̌ŗL�l��@�Ɣ�r����ƁA���̂悤�ȓ����������Ă���B
�����@�@�听�����͂Ȃǂ̑��ϗʉ�͂́A�����������\������ϐ��̑����̖��������āA���������߂邱�Ƃ�ړI�ɂ��Ă���B�v�����͂��s���Ƃ��A�݂��ɑ��ւ̂���ϐ���p����ƁA��^�������d�ɂȂ�̂ŁA�Ɨ��������������߂ėv�����ʂ����邱�Ƃ͏d�v�ȗv���ł���B�p��̖��P�O��A���w�̖��T��̊w�̓e�X�g�̏ꍇ�A���v�_���o���ƁA�p�ꂪ���ӂȐl�͂P�O�_�A���w�̓��ӂȐl�͂T�_�ɂȂ�̂ŁA�P���ɍl���āA�p�ꂪ���������o���Ȃ��l�Ɛ��w���_�̐l�Ƃ������ɕ]�������B�p����d��������w�����ɗ��p�������@�ł���B���̓��_��\�͂ŕ\������Ƃ��ɂ́A��萔�̑����̖��������K�v������A�听�����_�͂��̂悤�ȓ��_�ł���B�m�\�i�\�́j����舵���Ƃ��A�s�꒲���ȂǂŁA���ڐ������O�ɒ����ł��Ȃ��Ƃ��ɂ́A�听�����͌n�̕��@���g���B
�@����ɑ��āA��L�̖�萔�f������ꍇ�A�������Ȃǂ̔����w�����̑召�f�����镪�͂Ȃǂ́A�ʏ�̑��ϗʉ�͂ł���悤�ȕW���������Ȃ��ŁA�f�[�^�̐Ϙa�i�O���������Ƃ�\���w�W�j���听�����͂���A�f�[�^�̓x���̑傫���i�{�����[���j���ł��悭�����ł��鎟�������߂邱�Ƃ��ł���B���݃N���X���͂́A���̂悤�ȃ{�����[����������鎲�����߂���@�ɑ�����B
�����A�@��ʂ̑��ϗʉ�͂́A�ϐ��Ԃ̓����o���i�Q�̍��ڂɊY������A���Ȃ��Ƃ������Ɓj�𑊊֊W�ƍl���āA���̑��ւ���菜�����Ƃ�ړI�ɂ��Ă��邪�A���݃N���X���͂́A�����o���̕������N���X�����Ɋ�^�̑傫�ȕ��U�ƍl���āA�����ϋɓI�Ɏg���B���������āA�����o���̑������ڂ��N���X�����ɑ傫�Ȗ����������ڂƍl����i�ʏ�̎听�����͂́A�����o���̍��ڂ͂ǂ��炩�̍��ڂ������Ă��������ʂɂȂ�j�B���݃N���X���͂ł́A�����o�������֊W��\�����Ă��Ȃ����Ƃ��A�Ǐ��Ɨ��i�{���I�ȍ��ڊԑ��ւ͂Ȃ����Ɓj�̉���ƌ����Ă���B
�@���̂��Ƃ́A�d��A���͂Ȃǂ́u�Ɨ��ϐ��v�Ɠ����l�����ł���B�d��A���͂Ȃǂł́A�Ɨ��ϐ��Ԃ̑��ւ��u��������̑��ցv�Ƃ��Ď�菜�����A���݃N���X���͂ł́A���ڂ̓Ɨ����͕ۂ���Ă���Ɖ��肷��̂ŁA�����o���́A�Ɨ������̓����I�D���ʂł���Ƃ��āA�����͖ړI�ɂ���B
�����B�@���݃N���X���͂ł́A�Q�̍��ڂ̓����o���ɉ����āA�R�ȏ�̓����o���̕������d������B�����I�ɂ́A�S�ȏ�̍��ڂ̓����o�������ʂɔ��f�����邱�Ƃ�����̂ŁA�R�܂ł̃f�[�^��p����B�������A���ׂĂ̍��ڂ��l���ł��Ȃ��̂ŁA�R�ڂ̍��ڂ͂ǂꂩ���p���邱�Ƃ���ʓI�ł���B��q�̖{���Œ�Ă�����@�́A�R�d�N���X�̑S���ڂ��ϓ��ɍl��������@�ł���A�S�d�N���X�A5�d�N���X�̕����\�ł���B
�i���݃N���X���͂̐Ϙa�R���听�����͂ɂ���@�j
�@�ȏ�̐����̂悤�ɁA���݃N���X���͂́A�Ɨ����������̔����p�^�[���i�P�P�O�O�P�Ȃǁj���J�E���g����悤�ȕ��@�ł���A�{���Ō������ϗʉ�͂ł͂Ȃ��A�x���W�v�̗v��Ƃ����悤�ȓ����������Ă���B
�@�R�d�N���X�\�̓x���́A�R���R���X�|���f���X���͂�K�p����ƁA����ʁA�P�����ݍ�p�A�Q�����ݍ�p�����āA�R���听�����́i�P��̋�Ԃ����肷����@�A�������u�f�[�^���͓���Q�v�Q�Ɓj��K�p���邪�A���݃N���X���͂̏ꍇ�ɂ́A����ʂȂǂ���菜���Ȃ��R���听�����͂�K�p����悢���Ƃ��킩��B���������āA�R�d�N���X�\���A���̂܂ܓ��̓f�[�^�Ƃ��āA�Ϙa�̂R���听�������߂邱�Ƃɂ���āA�����Ƃ��ł���B�u�f�[�^���͓���Q�v�ɂ���悤�ɁA�S���ȏ�̃f�[�^�ɂ���r�I�ȒP�Ɉ�ʉ��ł��邪�A���ۂ̃f�[�^�ł́A���ݍ�p�������ꍇ�i�f�[�^�������Ȃ�������A�덷�Ƃ��čl������ꍇ�Ȃǁj�Ƃ��ĉ��߂ł���̂ŁA�R�d�N���X���x�̃f�[�^�ɂ���āA�\���A���݃N���X���K��ł���ƍl������i�ꍇ�ɂ���ẮA�P���W�v�\��A�Q���N���X�\�݂̂ŏ\���Ȃ��Ƃ����蓾��j�B
���ݕϐ�latent variable��S���w�I�A����psychological continuum��S���ړxpsychological
scale
�@�Ⴆ�C���~����100�_���_�̃e�X�g�ɂ��āC�w�͂ɂ���āC50�_��60�_�ɂ���ꍇ��90�_��100�_�ɂ���ꍇ���r����ƁC90�_��100�_�ɂ���ꍇ�̕��������I�ɓ�����Ƃ�������D���̏ꍇ�C���Ԃ�w�͗ʂɂ���Ď��͂͑������邪�C100���߂��ɂȂ�ƁC������Ƃ���ʂɁC�䗦�̓��_�́C���W�b�g�͐l�ԍs���̗v�����͂��s���Ƃ��C��ʂɑ��肳�ꂽ���l�ł͂Ȃ��C�����I�Ȑ��ݕϐ��ɂ��čs�����Ƃ������D���Ō����C�͂��߂ĕ������鉹�̑傫���D�h��臂Ƃ������D���ɍ����C�d���C���̑��̊��o�ɂ��Ē�`�����D���ۂ̑���ł́C�������鉹�ƕ������Ȃ��������m�ɋ�ʂł���킯�łȂ��̂ŁC�����̑��茋�ʂ��瓝�v�I�Ɍ��߂���D����@�ɂ��Ă̐S����������@�⊯�\�����@�ȂǁC���茋�ʂ��M���ł���悤�ɁC���̎葱�����m������Ă���D�傫������臂��h�����Ƃ������Ƃ�����D���̑傫���Ȃǂł͎h�����̑���͂ł��Ȃ��̂Ő���l�ɂȂ�D���p�I�ɂ́C���臂������K���C�s������������͈͂̕����d�v�ɂȂ邱�Ƃ������D
���W��correlation coefficient
�Q�̕ϐ��̊֘A�x��\���W���D�Ή�����Q�̕ϐ��̕Е����傫���Ȃ�Ƃ���������傫���Ȃ�Ƃ��C�Е����������Ȃ�Ƃ���������������Ȃ�Ƃ����悤�ȌX���𑽂��̃f�[�^�̑��ΓI�Ȉʒu�̑召��p���ĕ\���������́D���W�����傫���Ƃ��ɂ́C�Q�̕ϐ��̌����ƌ��ʂ̊W�����邩�C�����̕ϐ��Ƃ͕ʂɋ��ʂ������������邱�Ƃ��������Ă���D
���֍s��\�쐬�i���Ђ̕��̓V�X�e�����j
���W���}�g���b�N�X���o�͂���V�X�e���D�召���̕��בւ����ł���D
���W���̌�������������D
����I��`
�l�Ԃ̍s���Ɋւ�����́C���t��C���[�W�i�T�O�j�ɂ���č\������邱�Ƃ������D����������ł́C��̓I�ȑ���ɂ���đ��肷��̂ŁC������̓I�ȑ���ɂ���Ēu��������K�v������i����I��`�j�D���_�ڎ��₵�āC�����邱�Ƃ��������C�҂��T�O�̈Ӗ��⎩���̓��ȓI�ȋ@�\�C���ʊW�̎����ȂǁC���l�Ƌ��ʂ������e�������Ă���Ƃ͌���Ȃ��̂ŁC����I��`�ɂ���āC�ԐړI�ɉ��߂�������q�ϐ��������C�M�������������Ƃ͗����ł���D���p��ł́C����I�ȑ�������C���ڂɈӎ����e�����₷�邱�Ƃ��K�v�ȏꍇ��C�L���ȏꍇ�������D
�o�Ύړx�@ dual scaling
�W�v�\�Ȃǂ̍s�Ɨ�̗������X�P�[�����O���ă}�b�s���O�\����������@�D�s�Ɨ�Ƃ����ւ��Ă������Ɏ�舵����̂Łi�o�ΐ��Ƃ����j�C�o�Ύړx�@�ƌ�����D�����\�̎����l����C���U���͂̋��ԕ��U���ő�ɂ���悤�ɍs�v�f�̓��_�𐄒肷��D�œK�ړx�@Optimal scaling�Ƃ�������D���ԕ��U���ő�ɂ��邱�Ƃ́C�f�[�^���������C�s�v�f�̓��_�Ɨ�v�f�̓��_�̑��ւ��ő�ɂ��邱�ƂƓ������D���������āC���ւ��ő�ɂ���Ƃ�����̐��ʉ��R�ނ̉������ƈ�v����D�܂��C���ւ��ő�ɂ��邱�Ƃ͍s�Ɨ�̑��݂̉�A���͂̌덷���ŏ��ɂ��邱�Ƃɂ��Ȃ�D���ւ��ő�ɂ��邱�Ƃ��A�̌덷���ŏ��ɂ��邱�Ƃ́C�s�Ɨ�̍��W�l�𐔒l�I�ɂł��邾���߂Â��邱�Ƃ��Ӗ����C���������āC�l�c�r�̓W�J�@�̉������̈�Ƃ�������D�l�c�r�̌n���ł́C�����O�E�n�E�X�z�E���_�[�̋����ƍ��W�l�Ƃ̊W������C�d�S�����_�Ƃ������W�l���ŗL�l�ƌŗL�x�N�g�����������Ƃɂ���ċ��߂���D�R���X�|���f���X���͂́C�s�Ɨ�̗�����������C�ŗL�l�C�ŗL�x�N�g���i�听�����́C�����O�E�n�E�X�z�E���_�[�̒藝�j�ɂ���āC�s�Ɨ�̓����z�u�����߂�D�f�[�^��������Ȃ��ł��̂܂܋�ԕz�u�����Ƃ߁C��P�����ڂ��C�X�P�[���t�@�N�^�[�Ƃ��ď������Ƃ��l������D�����̕��@�́C�قȂ����A�C�f�B�A����\�����ꂽ���@�ł��邪�C��{�I�ɑ��ϗʉ�͂ő����p�����镪�U�ő剻�̊�ɏ]���̂ŁC����f�[�^�̈Ⴂ�ƕ��͌��ʂ̕\���@���قȂ邪�C������@�ɂȂ�D���̈Ӗ��ł́C�f�[�^��K���ɕϊ�����C�����̕��͖@�́C�������֕��͂Ɖ������ɂ���ĉ������Ƃ��ł��C���ʉ��Q�ށC���d���ʕ��́C�d��A���́C���ʕ��͂ȂǂƂ�������Ƃ��Ĉ�ʉ����邱�Ƃ��ł���D���p���鑤���炷��ƁC���Ȃ���̓v���O�������ǂ̗v���ɂ��Ή��ł���̂ŁC���ɕ֗��ł���D
�o�Ύړx�@�ƃR���X�|���f���X���́E���ʉ��R�ނƂ̊W���u���ʉ�3�ށE�R���X�|���f���X���́E�o�Ύړx�@�v�Q�ƁD
�� mode�ƌ� way
���̓f�[�^�̌`��\������Ƃ��ɗp������D�Q���f�[�^�C�R���f�[�^�ȂǁD��mode�́A���肳���W����\�킷�Ƃ��ɗp�����邱�Ƃ������B���֍s��́A�Q���̌`�����Ă��邪�A�s�v�f�Ɨ�v�f�������Ȃ̂ŁA�P���f�[�^�ƌ�����B�����̃u�����h�ɂɂ��āA�����̕]�����ڂɂ���āA�����̐l���]���������ʂ́A�����̂̃C���[�W�ɂ���ăf�[�^��\���ł���̂ŁA�Q���f�[�^�ł���A�e���͈قȂ����W���̗v�f�ɂȂ�̂ŁA�R���f�[�^�ƌ�����B�]���҂�N�ߕʁ~���ʂȂǂ̑����Ƃ��đ������ꍇ�A�S���f�[�^�Ƃ��Ă��ĕ\���ł���B�܂��A�S���f�[�^�ƌ�����B���ۂ̕��͂ł́A���⑊�̊T�O�����܂�C�ɂ��Ȃ��ŕ��͖@�𗘗p���邱�Ƃ��ł���B���Ȃ݂ɁA���̗p��́Aphase�̖�ɗp�����邱�Ƃ�����A�����͈قȂ����Ӗ��ł���B�R�����q���́C�R���R���X�|���f���X���́A�R���听�����͂Ȃǂ̍��Q�ƁD
���̒lj��i�R���X�|���f���X���́j���O�������R���X�|���f���X���́D
�w�ʕ��ςƑ��ւƂ̈Ⴂ
�w���ӌ��Ɛ��i�̓����Ƃ̊֘A���������Ƃ��C�w���ӌ��̍����l�̐��i�����̕]�����ʂ����āC���ϒl�̑傫���������C�w���ӌ��̌����ł���ƍl���₷���D�������C�w���ӌ��̒Ⴂ�l������ƁC��͂蓯�����ڂ̕��ϒl�������ꍇ������D�w���ӌ��̌����́C���ӌ��҂ƒ�ӌ��҂̓����]���̍����݂�K�v������D�����i�v�����ʁj�̕��͖@�ł��鑊�W���C���U���͂Ȃǂ́C��ΓI�Ȑ����ł͂Ȃ��č��̑召����ɂ���D
����l�̕���
�@����l�́A���͖@�i���胂�f���j�̈Ⴂ����A�}�̂悤�ɂS�ɕ�������B��{�I�ɂ́A�}�C�i�X�̂Ȃ��x���E�{���n�ƐS���ړx�Ȃǂ̕s�ώړx�n�̂Q�ɂȂ�A�ΐ����E�w�����ɂ���Č��ѕt������i�|�A�\�����f���E�ΐ����`���f���E�t�F�q�i�[���f���Ȃǁj�B�䗦�n�̑���l�́A�ΐ����f���𑪒�̏ɓK�p�����ꍇ�Ƃ��ė����ł���B�����ł̕��ނ́A���͖@�ƈ�v���Ă��邱�Ƃ������ł���̂ŁA���`�ړxnominal
scale�ƌĂ�鑪��l�́A���͂���Ƃ��ɂ́A�x���E�{���ړx�␔�ʎړx�i�s�ώړx�j�̂ǂ��炩�ɕ��ނ����B�����́A�u�I���̏��ʁv�Ɓu�ٕʂ̏����v�ɕ������āA���ꂼ��A��舵�����@�i���f���j���قȂ��Ă���̂ŁA�\���̂��߂ɂ́A�K�������f����p����K�v������B�i�u�S������̊�b�ƒ����ł̉��p�v�N�R2009�Q�Ɓj�B
Home�@���������@��ЊT�v�@�A�s�@�J�s�@�T�s�@�^�s�@�i�s�@�n�s�@�}�s�@���s�@���s�@���s�@�Q�l����