���Ђ̋Ɩ��Ŏg�p���Ă���p���������Ă��܂��D
Home�@���������@��ЊT�v�@�A�s�@�J�s�@�T�s�@�^�s�@�i�s�@�n�s�@�}�s�@���s�@���s�@���s�@�Q�l����
�A�Z�b�T�[Assessor
�V���i�̃}�[�P�b�g�V�F�A�̐���V�X�e���D���Ђ̗\���V�X�e���́C���������ƂɓƎ��ɊJ���������̂ł���̂ŁC�A�Z�b�T�[���̂��̂ł͂Ȃ����C�͋[�X������`�b�v�Q�[���ȂǁC�����ɏ]���Ď��{����悤�ɂȂ��Ă���D�uB-02�}�[�P�b�g�V�F�A�\���V�X�e���v������D�uB-03�}�[�P�b�g�V�F�A�\���V�X�e���v�@���ʂ̂܂Ƃߕ��D�uC002�����I�}�[�P�b�g�V�F�A�\���V�X�e���v�@�Z�~�i�[�e�L�X�g�Ƃ��č\�����ꂽ������D���n��v�f���܂�ł���̂ŃA�Z�b�T�[�Ƃ͈قȂ������̂ɂȂ��Ă���D
�`�k�r�b�`�k(�A���X�J���Aalternating least squares scaling)
�l���͂ł���l�c�r�̃v���O�����D��@�Ƃ��ẮC�m�����g���b�N�����Ƃ��ĒP����A�@�Əd�ݕt�������̉�@�Ƃ��Č��ݍŏ��Q��@��p���Ă���D���p��̉��p��͂��܂葽���Ȃ��D�i�������u�������ړx�@�v����o�ŎQ�Ɓj�D���l�c�r�i�G���f�B�[�G�X�j�C�P����A�@�C���ݍŏ��Q��@�Ȃǂ̗p��Q�ƁD
�Ɠ_saddle point
�P�̕ϐ��̏ꍇ�̂Q�����́C�w�I�ɂ͕�������\������iy=a(x-b)2+n�j���C�Q�̕ϐ��̏ꍇ�̂Q�����i
y=a(x1-b)2+c(x2-d)2+n�j�ł́C�萔a�Cc�̕����ɂ���āC���̕`���w�I�Ȍ`���قȂ�i�O���W�J�@�̍��ڎQ�Ɓj�D���p����ꍇ�ɂ́C���̕\������`���̂��d�v�ȈӖ������D�Q�̎����̂Q���̍��̌W���ia�Cc�j���v���X�ƃ}�C�i�X�̑g�����ɂȂ����Ƃ��C�w�I�ɂ͈Ƃ̌`�̋Ȗʂ�`���D�O���W�J�@(external
unfolding method)�ɂ����āC�œK�l�i�n�D�_�j�����߂�Ƃ��C�Q�̎����̕Е��͍Śn�D�_�C�Е��͔�n�D�_�ɂȂ邱�Ƃ����邪�C����́C�����̃E�F�C�g���v���X�ƃ}�C�i�X�ɂȂ�Ƃ��ł���C�n�D�X���̃��f�����Ƃ̌`�ɂȂ邱�ƂɂȂ�D���ʏ�Śn�D�������ꏊ���Q�J������C�������œK�Țn�D�_���ݒ肳�ꂽ���ʂ̊O���ɂ���Ƃ��C�Q���Ȑ����f���ɂ���ċL�q����ƈƓ_���f�������Ă͂܂�D���ۂɑ����̌l�̍œK�_�����߂�悤�ȏꍇ�ɂ́A�Ɠ_��z�肵�����f���͗��p���Â炢�̂ŁA�œK�_���P�_�ɂ��郂�f�����g�����Ƃ������D�n�D�X���Ɋ��`��K�p����̂Ƃ͕ʂɁC�n�D�̖��x���i���z�j��z�肵�����f��������D���̏ꍇ�̑o��^���f���͐}�̂悤�ɂȂ�D
臒l�i�������jthreshold,limen
�u���臁v(absolute threshold)�͎h���̑��݂������鋭�x�D�u�ٕ�臁vdifference
limen�͎h���̈Ⴂ��������h�����x�̂��ƁD�����������n�߂ĕ������鋭�x�C���邳�C�d���ȂǁC���o�̐��臂𑪒肷�邱�Ƃ��ł���D�ٕ�臂𑪒肷��Ƃ��C����̎h���ł����Ă������悤�Ɋ�������قȂ��Ċ������肷�邱�Ƃ�����̂ŁC�����ł��Ȃ��v���ɂ���Ďh���┽�������ł͂Ȃ����K���z����Ɖ��肵�Ă���D�����̌J��Ԃ������ɂ���āC���K���z�̕��ςƕ��U�𐄒肵�C臒l���`���邱�Ƃ��C�Â�����s���Ă���D�P��@�Q�ƁD�S����������@�Q�ƁD
�֎q�̌`�ԃC���[�W�̕���
�R�����q���͂��֎q�̌`�ԕ]���ƕ]���̌l���̖��ɉ��p������D�����ԍ�E021�Q�Ɓi�����_��������j�D
�C�X�̂p�c�`
�֎q�̍���S�n�ɂ��Ă̕]�����@�D���悻�R�O���ڂ̕]���ړx�ƁC���͖@�C���ʂ̕\���@�C���������̌��ߕ�����ѓK�p��D�C�X�̍���S�n�̊��\�����@�D�]��@�̂��]���D�C�X�̂p�c�`�D�uC-02�f�[�^���͓���v5000�~�ɊȒP�ȓK�p�Ⴊ����B�uJ-15�֎q�̕]���@�v�Q�ƁD
�ꌳ�z�u���U����
���鑪��l��E�Ƃ̂悤�ȕ��ޗv���ɂ��Ă̍����݂�Ƃ��P�v���̕��U���͂�p����D�f�[�^�̕��U�i���Q��a�j���e�E�Ƃ��Ƃ̃o���c�L�ƐE�ƊԂ̃o���c�L�ɕ����āC�E�ƊԂ̃o���c�L�����R�덷�ȏ�̑傫���ɂȂ��Ă��邩�ׂ�D�m���͂e���z��p����D�����팱�҂����ׂĂ̎h���ɂ��ĕ]�����Ă���ꍇ�ɂ́C�Q�v���̕��U���͂�K�p�����������o�͂����܂�D�P�v���̕��ϒl�̍��̌���ɂ́uM-16���ϒl�\�v�Z�V�X�e���v��p����D���d��r����i�t�B�b�V���[�̂k�r�c�j�������Ɍv�Z�ł���D�uA-65���U���͖@�v�́A���U���͖@�̂��S�ʓI�ȉ���D�uA-63���U���͂ɂ����鑽�d��r�v�͑��d��r�̈Ӗ��̉���D
�P�����}�b�s���O
���l���P�����̐�������Ɉʒu�t����D�Q�����̃}�b�s���O�}�b�s���O�\���ɑ��ĂP�����̃}�b�s���O�ƌ�����D�uA-03�|�W�V���j���O�V�X�e���v������D�uM-08�|�W�V���j���O�V�X�e���v�}�j���A���D
�P�����q�s�� (one-mode factor matrix)
�R�����q���͖@�̊T�O�̒��ŁC�P�̑��݂̂����q���������_�s��D�ʏ�̈��q���͂̈��q���_�Ɠ����ł��邪�C�R�����q���͂̏ꍇ�ɂ͐Ϙa�s��͂���D�uA-70 �R�����q���͖@�v�́A�R�����q���͖@�̉�����D
���r�@paired comparison method
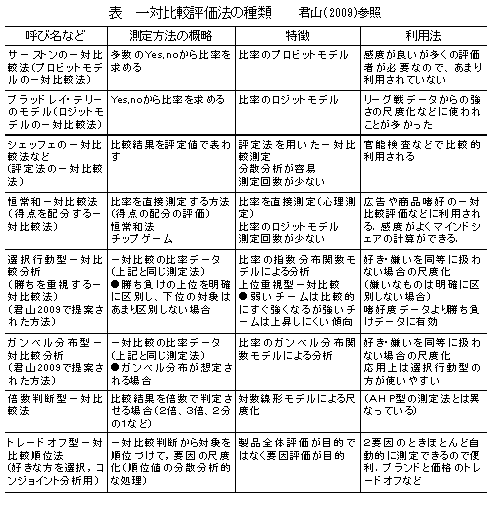
�@���(�Q��)�̎h�����r���đ��ΓI�ɕ]������葱���ɂ���đΏۂ̚n�D�x�Ȃǂ𑪒肷����@�D�����ȍ��ق�]������̂ɓK���Ă���D���ɑ��ăv���r�b�g���f���i���K���z�̊����j��K�p����T�[�X�g���̕��@�A���W�b�g���f����K�p����u���b�h���[�E�e���[�̕��@�A�]��@��K�p����V�F�b�t�F�̕��@�A�����_��z�����Ĕ䗦�ڑ��肷��P��a��Δ�r�@�i�`�b�v�Q�[���̈�Δ�r�@�j�A�䗦�Ɏw�����z�����f����K�p����I���s���^��Δ�r�@�i�N�R2009�̕��@�j�Ȃǂ�����B
�@���������A���i�̔�r���ʂȂǂł́A���W�b�g��v���r�b�g�����I���s���^��Δ�r�@���K���Ă���ƍl������i�N�R2009�u�S������̊�b�ƒ����ł̉��p�v�Q�Ɓj�B
�@���ꂼ��A���̕��@�Ƃ͈قȂ��������������Ă���̂ŁA�g�������邱�Ƃ��L���ł���B
��ʉ�����W��generalized coefficient of determinant
�@�������֕��́A���ϗʉ�A���́A���ϗʕ��U���͂ȂǁA���ϗʂ̖ړI�ϐ��Ƒ��ϗʂ̐����ϐ��̊W��\������̎w�W�B�������W���̂Q��i�֘A�x�s��̌ŗL�l�j�����Z���āA�����N�Ŋ��������l�B1�ϗʂ̏d���W���̂Q��i����W���j���听�����͂̑������̊�^���̂悤�ɁA���R�Ȍ`�ň�ʉ��������́B���̂悤�ȓ���������B
�@�ړI�ϐ��Q����ْl�����i�听�����́j���āA�����������߁A�ʁX�ɏd��A���͂�K�p�����Ƃ��́A����W���̍��v�l�̊����ɂȂ�B
�A�ړI�ϐ��Q�̌ŗL�l�́A�S�ϐ��̕��U�̍��v�������ɔz�����邱�ƂɂȂ�̂ŁA�S���U�̎������Ƃ̐��������Ӗ����Ă���B���������āA�ŗL�l�̑傫�������Ă��邪�A��{�I�ɁA�ړI�ϐ��Ԃ̑��֊W���l�����Ă��Ȃ��̂Łi���ւ��������ړI�ϐ��̕��U���S�����f����Ă���j�A�������i��ʉ�����W���j����⏬���߂ɂȂ�Ǝv����i��ʓI�ȑS���U�́A���֊W���l������ƌŗL�l�̍��v��菬���߂ɂȂ�j�B
�@���ϗʂ̕��U�́A��ʉ�����W���̂悤�ȌŗL�l�̉��Z�n�ł͒�`�ł��Ȃ��ƍl���āA���ϗʐ��K���z��z�肵�āA�ړI�ϐ��Ԃ̋����U�s��i���֍s��j�̍s����ʓI�ȕ��U�Ƃ��āA�����ł���傫�����`����E�B���N�X������x�N�g�����W���Ȃǂ�����B�E�B���N�X������s�i��ʉ����U�j�́A�ʏ�̕��U�̂悤�ɁA�x�N�g�������łȂ��̂ŁA�w���^���z�̖ޓx�ɊW�����ΐ����`�ȉ��Z�����S�ɂȂ�i���|���Z�����S�j�B
��ʉ����ْl����
�@�������֕��́A���ϗʉ�A���́A���ϗʕ��U���́A�d���ʕ��́A���ʉ��Q�ށA�R���X�|���f���X���͂Ȃǂ̑��ϐ��Ԃ̊֘A����舵�����@�́A��ʉ��ŗL�l���ɋA������B��ʉ��ŗL�l���́A�ȉ��̎��̂悤�ɁA���U�����U�s��i���֍s��j�̕������s��ɂ��ϊ��ɂ���āA�ʏ�̌ŗL�l���Ƃ��ĉ������Ƃ��ł���B�ʏ�̌ŗL�l���ɑΉ����ē��ْl����������悤�ɁA��ʉ��ŗL�l���ɂ��Ĉ�ʉ����ْl��������Ă���Ă���B���U�����U�s��̕������s��ɂ��ϊ��́A���ϗʂ̕W��������ɂ�������̂ŁA�P�Ȃ�v�Z��̖�肾���łȂ��A�R���X�|���f���X���͂ɂ݂���悤�ɁA����ϊ����̂ɗL���ȈӖ�������i���ϗʉ�A���͂̍��Q�Ɓj�B�ȉ��̎��́A���ɕ��U�����U�s��ɂ��āA��ʉ����ْl������������Ă���B

�C�f�B�I�X�J���i�h�c�h�n�r�b�`�k�j
�l�����l�������l�c�r���f���̃m�����g���b�N�v���O�����B�m�����g���b�N�A�l�c�r�ȂǎQ�ƁB
�C�{�[�N�g�Z�b�g(evoked set)
�z�N�W���Ɩ��D���Ƃ��C�V�F�A�𐄒肷��Ƃ��ɕ]���ΏۂƂ��čl�����鋣�����i�Ȃǂ̓C�{�[�N�g�Z�b�g�ƌ�����D����l�̓C�{�[�N�g�Z�b�g�̒��Ő��肳���D�قƂ�ǂ��ׂĂ̋������i���܂�ł���Α��肳�ꂽ�}�C���h�V�F�A�͂��̂܂s��ɓK�p�ł��邪�C�S�̂��J�o�[���Ă��Ȃ��Ƃ��ɂ́C���炩�̕ϊ����K�v�ƂȂ�D
�C���[�W�w���@(���Ђ̒������ʂ̕\���@���j
���Ђ̃C���[�W����@�̖��O�B�C���[�W���荀�ڂ̊Y���������߂āA������C���[�W�w���Ƃ����B�P�O�O�_���_�ɂȂ��Ă���B�قȂ����̈�̑Ώۂɂ��Ă���r���邱�Ƃ��ł���B�uJ-17�C���[�W�̑���@�@���q���͂ƃR���X�|���f���X���́v5000�~�B�Q�ƁB
�C���[�W����ɂ��}�C���h�V�F�A�\��
�C���[�W���_���㉺�����邱�Ƃɂ�镡�����i�̃}�C���h�V�F�A�̃V�~�����[�V�����V�X�e���B�����ɂ���āA�������鐻�i�̃C���[�W�𑪒肵�A���݂̃V�F�A�i���W�b�g�ϊ��j�⒲���ɂ��w���ӌ��A�n�D�x���茋�ʂȂǂ��O�I��ɂ��āA�E�F�C�g�𐄒肷��B���̌�́A�\���������ɂ���Ěn�D�x��V�F�A��\������B�n�D�x�́A���v���P�O�O�ɂȂ�悤�Ȑ�������Ă����ĉ������A����l���Βl�ϊ����Ă���V�F�A�̌`�ɕϊ�����B��Βl�ϊ��ɂ̓x�L�����p������B�uB-16�@�C���[�W����ɂ��}�C���h�V�F�A�̗\���V�X�e���v�B
���ʊW�Ƒ��֊W
���ʂ͐l�Ԃ̌���̈Ӗ��i�\���T�O,�����j�ɑ�������ŁA���ڑ��肷�邱�Ƃ��ł��Ȃ��̂ŁC����I�ɒ�`����ƁC���ԓI�O��i�������O�C���ʂ���j�C���ԊԊu���Z�����ƁC���̌��ۂ̓����I���N�̗L���ȂǁC�m���ɒ�`���邱�Ƃ�����D���ʂ̊T�O���̂́C�ώ@�ł���l�X�Ȍ��ۂ���C�L���ŕ֗��Ȃ��̂Ƃ��č\�����ꂽ�̂ł��邪�C�����̂��Ƃ��āC�g���Ă���D����ɑ��āA���֊W�́A�Ή�����f�[�^�̋��ϓ��I�ω��Ƃ��āC�Ӗ��Ƃ͕ʂɒ�`����Ă���̂ŁA���ʊW�Ƃ͖{���I�ɈقȂ����T�O�ł���D�������A��X�������Ă�����́A���ʂ̂悤�ȈӖ��̂���T�O�̃��x���Œ�o�����̂ŁA��ʓI�ɂ́C�u���ʊW������A�K���ȏ����̉��ŁA���֊W���ώ@�����͂��ł���v�i�����j�ƍl���āA���֊W���ώ@����Ƃ����葱���ɂ���Ĉ��ʊW�������邱�Ƃ��s����D���������āC�����ɂ́C���ʊW�����ڂɏؖ����ꂽ�̂ł͂Ȃ��C�������ے肳��Ȃ��Ƃ����Ӗ��ň��ʊW��F�߂�Ƃ������ƂɂȂ�D�����̉��p��ʂł́C���ʂ́C���Ԃ̊T�O�قǂł͂Ȃ��ɂ��Ă��C�ɂ߂Ĉ��肵�Ă��ėL���ȊT�O�̂P�ƌ�����D
���q���̌���@
���q���͂�����ꍇ�A�L���Ȉ��q�������肷�邱�Ƃ�����ꍇ������B���q�̍\�������m�ȏꍇ�̓f�[�^�ɂ����q��Ԃ̌��Ɨ\���̂��߂̕��͂ɂȂ邪�A�����̏ꍇ�A���q�����O�����ĕ�����Ȃ��ꍇ�������B�听�����͂����āA�����̊�^���̐��ڂ��O���t�ɂ��āi�X�N���[�v���b�g�C�ŗL�l�̌����X���̓ʉ���\�킵���}�j�A�}�Ɍ�������O�܂ł̎�����z�肵�A����ȍ~�͌덷�Ƃ�����A�ŗL�l���P�ȏ�̎��������q���ɂ����肷�邱�Ƃ�����B�ŗL�l�̋}���ȕω����J�C�Q�挟��ɂ���Ē��ׂ邱�Ƃ��ł���B�������A���ۂ̃f�[�^�ɂ����Ĉ��q�����قƂ�Ǘ\�z�ł��Ȃ��āC���荀�ڂ��\���ɖԗ�����Ă��Ȃ��ꍇ�A���q�̓��e�����f�[�^��v��ړI���d������ꍇ�ȂǁA���܂��܂ȃP�[�X������B���q���͂̓f�[�^�̗v��ɂ͋ɂ߂ĕ֗��ȕ��@�Ȃ̂ŁA�P��I�Ȉ��q�̒��o�ɂ͂��܂肱�����Ȃ��ŁA���p�I�ɍł��֗��Ɏg������q��p�������Ƃ����v���������B�l�X�ȃP�[�X�̈��q���͂ƈ��q���̕��͌��ʂ�����ƁA�f�[�^�S�̂̎����Ӗ����c���ł����Ƃ����m�M��������悤�ɂȂ�B���̂悤�Ȏ��s����I�ȍ�Ƃ���A�ł��g���Ղ��f�[�^�̈ꕔ�������������悤�ȕ�̂Ȃ����q���͌��ʂ�p����悤�ɂ��邱�Ƃ��d�v�ȍ�ƂɂȂ�A�K�R�I�ɁA���s����I�Ȉ��q������s���悤�ɂȂ��Ă��܂��B�uA-50���q���͖@�v�͈��q���͂̉�����D
���q����factor analysis
�{���C�s���̌����ƂȂ���ݓI�Ȉ��q��T�����@�ł���C�m�\���q�Ȃǂ͂��̓T�^�ł���B�������A�����̉��p�P�[�X�ł́C���q���̂��̂������ɍs���̌����ƍl���Ȃ��ŁC�����̑��荀�ڂ��r�I�����̌Q�ɕ��ނ��āC�]���Ώۂ̑S�̑��𗎂��x�Ȃ�������₷���c�����邽�߂ɗp���Ă���D���̂悤�ȗ��p�@�ł́C�]���Ώہi�Җ{�l���]���Ώۂł���ꍇ������j�̓��_�����߂āC�]���Ώۂ̈Ⴂ���������邱�Ƃ��ړI�ł���̂ŁC�v�ꂽ���_�i���q���_�j�����߂邱�Ƃ����q���͂ł���Ɣc������Ă���D��ԓI�ʒu�Ƃ��ĕ]���Ώۂ�\�����邱�Ƃ������̂ŁC�听�����́C���邢�͐��ʉ��R�ށC�R���X�|���f���X���͂ȂǂƁC��͏㎗�Ă���_�����邪�C���p��̓����͂��Ȃ�قȂ��Ă���D���W���͂���ƁC����ړx�i���ځj�̌��_����Ō��߂�̂ŁA��Ԃ̕����݂̂��Ӗ��������ƂɂȂ�D�f�[�^�̐Ϙa�s��͂���ƁC���_���Ӗ��������C�ϐ��x�N�g���̒������Ӗ�������̂ŁC���q���͂̈Ӗ������قȂ��Ă���D�uA-50���q���͖@�v�͈��q���͂̉�����D�uM-10���q���͂̃v���O�����v�̓v���O����������D
�@���q���͖@�͏�L�̂悤�ȍs���̌����ƂȂ���q�����߂邽�߂̕��@�ł��邪�C�f�[�^���͑���Ƃ��ẮC�����̃e�X�g�i����l�̃[���_��P�ʂ����ʂ��Ă���Ƃ͌���Ȃ��j�̑��W���s��C�@�ϐ��Ԃɋ��ʂ�����q�ɋK�肳��鑪��l�̕��U�i���ʈ��q��ԃx�N�g���̒����j�ɐ�����^�����C�A���q���̕����ɐ������Ȃ��C�B��̈��q������̂�������Ȃ��C�Ƃ����O��C�ϐ��̋�ԓI�Ȉʒl�����߂邱�ƂɂȂ�D���I����Ƃ��ẮC�t�ɏ�L�R�̏��������Ă��Ȃ��ƌv�Z�ł��Ȃ��̂ŁC���q�����݂���C��㈓I���ۓI�ɁC���W���̓f�[�^�̂悤�ɂȂ�͂����C�Ƃ���������㈓I�Ɏv�l���āC���s����I�ɉ������ƂɂȂ�D���Ƃ��C�T���q�����݂���Ƃ�����C�U���q��z�肷��ƁC1���q������̃f�[�^�L�q�̏��ʂ��i�i�Ɍ�������͂��ł���D�T���q�ł���ƕ���C�T���q��z�肵�āC���W���s����ł��ǂ������ł���ϐ��̋�ԓI�ʒu�����߂�C���ʐ��i���ʈ��q��Ԃ̕ϐ��x�N�g���j�����܂�i�����@�̎���q�@��Ŗސ���@�Ȃǁj�D��ԓI�ɂ́C���W���͔C�ӂł���̂ŁC�T���q��\�����鎲�i���q���j��T���悢�i�ϐ��x�N�g�����܂Ƃ܂��Ă��������T�����ƁC���̉�]�j�D���q�����m�ɑ��݂���C�ǂ̂悤�Ȏ葱�����Ƃ��Ă��C�������������悤�Ȉ��q�����o�ł���͂��ł���D���ۂ̃f�[�^�ł́C�@�T�O�I�ɂ͑��݂��z�肳��邪����f�[�^�̏���邩�Ȃ�������Ȃ����ƁC�A�����̃f�[�^�̈ꕔ���̃T���v���݂̂ɑ��݂��邱�Ƃ��z�肳��C�S�T���v���ɋ��ʂ��Ă��Ȃ����q�����邱�ƁC�B���q�����ݓI�Ȍ����Ƃ��������C���ɂ���ċ��ʂ��Č�����\�ʓI�ŕω����₷���s���X���𑨂��邱�ƁC�Ȃǂ̂��߂ɁC���m�Ȉ��q���K�肵�ɂ����D���������āC�f�[�^��v��Ƃ����悤�ȈӖ��ň��q���͂𗘗p����ƁC���W�����̂ɂ��덷��z�肵���C���U���͓I�i�听�����͓I�C�ŏ������ߎ��I�j�Ȉ��q���͖@���C���ۂ��ł����R�ɑ����C���W���̓ʉ��𑽎����I�ɔc�����邽�߂ɁC�֗��ȕ��@�Ƃ�����D���̌�ŁC�Ǝ������q��z�肵�����q���̓��f����K�p���邱�Ƃ��\�ł��邪�C���W���Ɍ덷������ƍl����ƁC�Ǝ����̍l�����̂���āC�傫���قȂ������ʂ��\��������D���̂��Ƃ�����C�Ó��Ȉ��q�̑傫�������߂�ƌ����O�ɁC���q�������邩�����Ȃ����U���͓I�Ɍ������邱�Ƃ��K�v�ł���D�����C���q�����肻���ȂƂ��ɂ́C��L�̈��q�̓����i�s���X���̒��g�j���l�����āC���莞�_�ɂ����āC�[���_�C�P�ʁC���ڂ̓Ɨ����Ȃǂ�z�����Đv����K�v������D���̂��Ƃɂ���āC����@�̉e�����������}�������p�I�ɗL���Ȉ��q�����o�ł���D
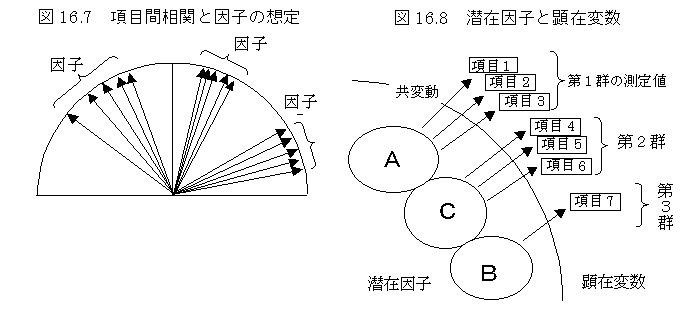
���q���͂Ǝ听�����͂̈Ⴂ
�听�����́iprincipal component analysis�j�́C�݂��ɑ��ւ��������̕ϐ����C�Ɨ����������̎����i�听���j�ɂ���ĕ\���������Ƃ��ɗp����D���i�����𑽐��̕]�����ڂɂ���ĕ]�������Ƃ��C�听�����͂�����ƁC���������Q������R�����ŕ\���ł��邱�Ƃ�����C��v�ȕ]�����������ł��邱�Ƃ��������Ă���D�Ӗ��̂��鎟�������Ȃ��ꍇ�i�f�[�^�S�̂��Q�����ŋߎ��ł���ꍇ�Ȃǁj���P�听���i�P�����ځj�����p��d�v�ȈӖ�������ꍇ�Ȃǂł́A�听�������̂܂g���邪�A�����̏ꍇ�A�听�����͂ł͈Ӗ��̂��鎟���ɂ͂Ȃ�Ȃ��D���������āA�听�����͂ɂ���Ď����\�������炩�ɂȂ�����C���̂܂܁C���̒�����]��Ό���]������ƁC���ʂ����p���₷���Ȃ�D���̉�]�Ȃǂ̑���͎听�����͂ł͂Ȃ��C���q���͂ƌ�����D���q���͖@�́C�Ӗ��̂�����q�����߂鑀��S�̂��w�����C���ʈ��q�ƓƎ�����z�肵�����q���̓��f�����������@�Ƃ��ĕ\�����邱�Ƃ��ł���D�听�����͂ɂ���ċ��߂�ꂽ��Ԃ����q�����߂�Ƃ����Ӗ��ł́C���q���͂̈�ł���ƌ����邪�C�听�����͂̏ꍇ�C�听�������߂����_�ő��W���ɂ��덷�����肷�邱�ƂɂȂ�̂ŁC�͂��߂��狤�ʐ������肵�đ��֍s��͂�����q���͂Ƃ́C��͏�͈قȂ��Ă���D�����Ȃǂ̑��ϐ�������q��T���ړI�̂��߂ɂ́C����ړx���̂Ɍ덷������ƍl���āC���͌��ʂ��狤�ʈ��q��Ԃ̑��֍s��i���ύs��j�����肳���Ƃ����听�����͂Ǝ��̉�]�́C�ϐ��Ԃ̑��݊W�����R�ɗ����ł��C���W�����傫���Ȃ��Ă��C�ϐ��Ԃ̑��ΓI�Ȃ܂Ƃ܂肪�����ł���̂ŁC�L���Ɏg������@�ł���D
�h�m�c�r�b�`�k�i�C���h�D�X�J��,individual differential scaling�j
�l�����l�������l�c�r�̃v���O�����D�ގ��x�s�l���Ƃɑ��肳�ꂽ�悤�ȂQ���R���f�[�^�̕��͖@�D���ׂĂ̌l�ɋ��ʂ����h���z�u�����߁C�����ɑ���E�F�C�g�̑召�Ōl����\���D��@�͐�������@(Canonical decomposition)�ƌĂ����@�ň��̌��ݍŏ��Q��@�ł���D�uA-69�l�����l�������������ړx�\���@�v�@�l�����͖@�̈�ɂh�m�c�r�b�`�k�����^����Ă���D�uM-22�h�m�c�r�b�`�k�v�̓v���O��������ł��邪�A���݃E�B���h�E�Y�ňȑO�̃x�[�V�b�N�`���ɂȂ��Ă���.�uA-01 �l�c�r�E���ϗʉ�̓J�^���O�v�C�uE-012�����̈��q�\���̔�r���́v�ȂǂɓK�p�Ⴊ����D
�E�F�C�g�o�b�N�W�v
�����Ώۂ̊�{�I�ȑ�������W�c�̍\����ƈقȂ����ꍇ�C�����\����ɂ�����@�Ƃ��āC�l�f�[�^�ɃE�F�C�g��^���ďW�v���邱�Ƃ��s����D����̏��i�̏��L���Ȃǂ̐���l�����߂�Ƃ��C���ʂ�N��Ȃǂ̓���ɕ肪����ƁC�P���ɑS�̂̐���l���v�Z�����,�肪������̂ŁC���ꂼ��ɈقȂ����E�F�C�g��^���āC�S�̂̍\������W�c�ɋ߂��Ȃ�悤�ɂ��Ă���C����l�����߂�D�v�Z��́C�P�T���v���̓x�����P�ł͂Ȃ��āC�E�F�C�g�l��p����D���ϗʉ�͂Ȃǂ̂قƂ�ǂ̕��͖@�ɂ��Ă��C�E�F�C�g��t�������͂��\�ł��邪�C���v�I��������̎��ɂ͎��R�x�͕ς��Ȃ��̂Œ��ӂ��K�v�ł���D
�u�a�`�i���C�E�r�[�E�G�[�Cvisual basic for application�j
�����ɁCMicrosoft Excel�̃}�N���Ƃ��Ďg�p�����r�W���A���x�[�V�b�N�DWord�CAccess�CPowerPoint�Ȃǂ̃\�t�g�E�F�A�ł��g����悤�ɂȂ��Ă���D���Ђ̕��͖@�́C���̂قƂ�ǂ��G�N�Z���}�N���̂u�a�`�ŏ�����Ă���D
�E�B�X�L�[�̃u�����h�C���[�W
���̑薼�D�u�d003�@�u�����h�C���[�W�̕��́v�D�R�����q���͂�p���ĕ��͂�������D�i�����_��������.1983�N�j
�`�h�b�i�G�[�E�A�C�E�V�[�CAkaike's infomation criterion�j�����ʊ�`�h�b
�`�h�c�i�G�[�E�A�C�E�f�B�[�Cautomatic interaction detector�j
�ړI�ϐ��i�w���ӌ��̋����Ȃǁj�ɂ��āC�N��C���ʁC����̍l�����ȂǁC�e���͂̑傫���v���ɂ���āC�Q���Ă����D�ŏI�I�ɁC�w���ӌ��̍����Q�ƁC�Ⴂ�Q�Ƃɕ������D�f�[�^�̌`���́C���U���͂␔�ʉ��P�ނȂǂƓ����D�Ⴆ�C�R�O��̏����݂̂ɑ傫����p���āC���̌Q�ɂ͂��܂��p���Ȃ��悤�ȗv��������Ƃ��C�����قǖ��m�ɂ��̕����𒊏o�ł��邱�Ƃ�����D���ϗʉ�͂ł́C�S�̂̃f�[�^�����ɂ��Ċ�^�������߂�̂ŁC�����I�Ȍ��ʂ𒊏o���邱�Ƃ�����D���̂悤�Ȉꌩ�����ɂ������ݍ�p�i�����I�Ȍ��ʁj�������I�Ɍ��o�ł��邱�Ƃ��C���̕��@�̓����ł���D���@�̖��O�����̂��Ƃ�\�����Ă���D
�@��r�I�����ɒ�`���ꂽ�Ɨ��ϐ��i�J�e�S���[�ϐ��j�̌��ʂ�O�O�ɒ��ׂ�ꍇ�i�����I�����ƚn�D�Ƃ̊W�Ȃǁj�ɓK���Ă���D�I���̊�l���r�I���܂�����ƁC���Ƃ��������������ꍇ�ɂ��Čo���I�ɗ������Ă��邱�ƂȂǂ����o�ł��邱�Ƃ��悭����D����ҍs���̌l�����͂���ƁC�^�[�Q�b�g�ƂȂ�Q�𒊏o���邱�Ƃ��ł���D�v�������ʁC�N��ʁC�Ȃǂ̃J�e�S���J���ϐ��ł���ꍇ�ɂ́C���U���͂�����Ԃ��v�Z�@�ɂȂ�C�A���ϗʂ̏ꍇ�ɂ́C���W���ƕ��ςɂ��Q�����̕��@���悢�D�ړI�ϐ����A���ʂłȂ��ꍇ�ɂ́C�ԂQ����𗘗p�������͂�C���U���͂ɂ�镽�ςQ�����@�Ȃǂ�����D�ړI�ϐ������ϗʂ̏ꍇ�ɂ́C�P�ϗʂ�P���ɌJ��Ԃ��Ă����͂��\�ł��邵�C���q��ړI�ϐ��ɂ��Ă����͂��邱�Ƃ��ł���D���̏ꍇ�C���ʉ��Q�ޕ��͂┻�ʕ��͂��X�̌Q�ɌJ��Ԃ��ēK�p���邷��̂Ɠ����ɂȂ�D�uA-19
�`�h�c�v(�^�[�Q�b�g����)��������D�uM-49 �`�h�c�̌v�Z�v���O�����v�͍�}�t���v���O�����D�}�́C���ʌ^�i�ړI�ϐ����Q�C100%���ށj�̂`�h�c�̗�ł��邪�C��A�^�̂`�h�c�ƌv�Z�@�͓����ŁC�f�[�^�̌`���قȂ�D
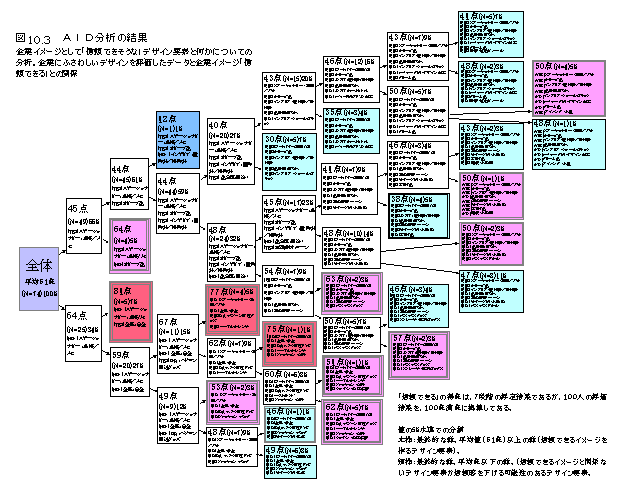
�`�h�c��p�����C���[�W�^�C�v�i�N���X�^�[�j����@�@
�@�U�J�e�S���[�i�N���X�^�[�j�̏ꍇ�A26/2-1=31�̑g�ݍ��킹������̂ŁA31��01�ϐ���ړI�ϐ��ɂ��āA����Ɏg�����ڂ̂`�h�c���͂��s���ƁA�����I�ɔ���}���쐬�ł���B���ϐ��̖ړI�ϐ��́A�P�ϐ��Ɠ���������J��Ԃ��B���̐}�̏ꍇ�A�`�h�c�ɂ��Q��25�Q�i�T���L�Ӑ��̎�����j�ɂȂ�A�ړI�ϐ��͂U�Q�ł���̂ŁA������N���X�\������āA�Ή�����Q�����߂�i�ł������Q�Ɍ��߂�j�B
�@���ݍ�p������ʂ��傫���ꍇ�ȂǁA�œK�ȉ��ɓ��B����ۏ͂Ȃ����A���s����I�ɕϐ���ς��Ă݂Ă��A�قƂ�ǂ̏ꍇ�A�K�����͈��ɂȂ�B
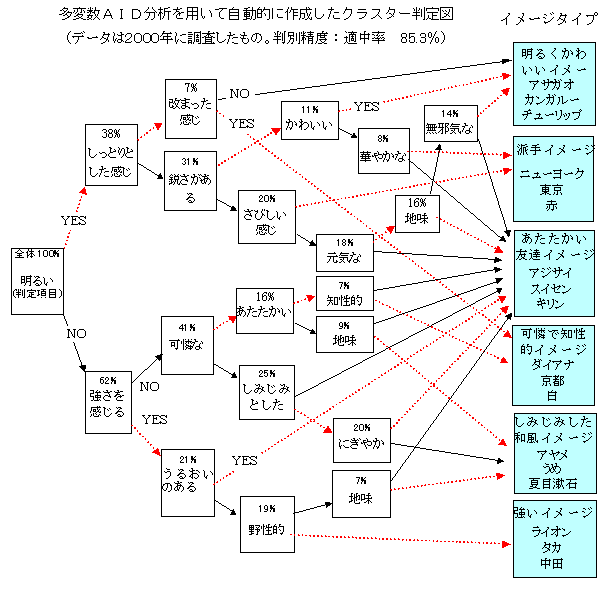
�r�l�b�i�G�X�E�G���E�V�[�Csquare multiple correlation�j�@
���q���͂�����Ƃ��̋��ʐ��i���֍s��Ȃǂ̕��͍s��̑Ίp�v�f�j�̐���@�D�r�l�b�̈Ӗ��́C�d���W���̂Q��D���֍s��̏ꍇ�C�Ίp�v�f�͂P�ɂȂ邪�C����́C�ϐ��x�N�g���̒�����\���C���v�I�ɂ͕��U��\���D���������āC���W���s��́C�����P�̃x�N�g���̂��ׂĂ̑g�ݍ��킹�̓��ρi�x�N�g���̎ˉe�j��\���Ă���D�Ƃ���ŁC���q���̓��f���ł́C�ϐ��x�N�g���́C���ʐ��ƌ�������q��Ԃ��\�����镔���ƓƎ����ƌĂ�邻�̕ϐ��݂̂��֗^���镔���Ƃɕ����Ă���D���������āC���q���͂ł́C����ꂽ���W���́C�������P�������������ʐ��ŕ\�����Q�̃x�N�g���̓��ρi�Ϙa�j�ƍl���Ă���D�听�����͂̏ꍇ�́C�e�ϐ��x�N�g���̕��U�����̂܂g����̂ŁC�f�[�^��菬���Ȏ����ŋߎ����ꂽ�听����Ԃ̊�^���i�������j�́C�S�ϐ����U�ɑ��銄���ŕ\�����邱�Ƃ��ł��邪�C���q���͂̏ꍇ�ɂ́C�S���U�����m�ł���S�ϐ��̋��ʐ��̍��v�l�ɂȂ��Ă��邽�߁C��^����������́C���ʐ��𐄒肵�Ȃ���C�v�Z���邱�Ƃ��ł��Ȃ��D�܂��C���ʐ������܂�Ȃ��Ɓi�x�N�g���̒��������܂�Ȃ��Ɓj�C���肳�ꂽ���W���i�x�N�g���̓��ρj�ɂ���ĕ\�������x�N�g���Ԃ̊W�i�݂��̊p�x�j�����܂�Ȃ��D���������āC���ʈ��q��Ԃ̑傫���i���U�j�⎟������܂�Ȃ��D���̂悤�Ȃ��Ƃ���C�Ó��ȋ��ʐ������߂邱�Ƃ����q���̖͂��̈�ɂȂ��Ă���D�r�l�b�́C��̕ϐ��ɑ��đ��̑S���̕ϐ�����̏d��A���͂̐������i�d���W���̂Q��C����W���j�����ʐ��̐���l�ɂ�����@�ł���D���q���͂́C�ϐ��Ԃ̊֘A���镔���i���ϓ����镔���j�̕��͂ł���C�d���W���̂Q�悪�C���̕ϐ������̕ϐ��Ɗm���ɋ��ϓ����镔���̑傫����\���̂Łi�d���ւ͂��̖ړI�ŋ��߂��鐔�l�j�C�덷���Ȃ��Ƃ��̋��ʐ��̉�����\���ƌ�����i���̐}�͂Q�ϐ��̏ꍇ�C���W�����Œ肳�ꂽ�Ƃ��̎��̋��ʐ��͈̔͂�\���Ă���j�D�r�l�b�̂ق��C���ʐ��𐄒肷����@�Ƃ��āC����̗�̑��W���̍ő�l��p����ꍇ�C�听�����͂ɂ���Č��߂���덷��Ǝ����ɂ���ꍇ�Ȃǂ����邪�C�����̈��q���͂ł͌ŗL�l�����������ʂ̋��ʐ���p���Ĕ����ߎ���������@���Ƃ��Ă���D���Ђ̈��q���͖@�ł́C�ǂ̕��@�ł��I���ł���悤�ɂȂ��Ă��邪�C�w�肵�Ȃ��ꍇ�ɂ́C���ʐ��͐��肹���Ɏ听�����́i���ْl�����j�����āC���ʐ���Ǝ�������ɂ���Ƃ��ɂ́C���q���חʂ̂Q��a�����ʐ��Ƃ��C���ʋ�ԂŐ����ł��Ȃ�������Ǝ����Ƃ���Ƃ������@���Ƃ��Ă���D�m�\�����Ƃ͈���āC�s�꒲���f�[�^�Ȃǂł́C���q���̓��f���ɂ���ĕϐ��Ԃ̈ʒu�W��ω���������C�ŏ��ɁC�ϐ��x�N�g���̈ʒu�W�ƁC���ʈ��q��Ԃƌ덷�Ƃ̊W�m�ɒm��K�v������̂ŁC���̂悤�ȕ��@���̂��Ă���D
�G�b�J�[�g�E�����O�����iEckert��Young�@decomposition�j
���肳�ꂽ�f�[�^�s����݂��ɒ���������v�f�̓��_�ƍs�v�f�̓��_�ɕϊ�������@�D�s���e���C�e���t���v�f�i�t���v�͌ŗL�x�N�g���s��C���͑Ίp�v�f�ɌŗL�l�̕�����������A���̗v�f���O�̍s��j�̌`�ɕ������邱�ƁD���p��́A���肳�ꂽ�ϐ��x�N�g�������̍��W�l�Ƃ��ė������邱�Ƃ�A�����i�������j�ɕ������邱�ƂƂ��ĉ��߂ł���B���U�̍ő剻�i���ւ���ς̍ő剻�j�C�덷�̍ŏ����������ɂ������͖@�ł́C���������̋ߎ����A�ŗL�l�̑傫�����̂��珇�Ɏg���悢�̂ŁA�����̑��ϗʉ�͂̊�{�I�ȉ�͖@�ɂȂ��Ă���B�v�Z�́A�ŗL�l�ƌŗL�x�N�g���i�X�y�N�g�������j�����߂邱�ƂɂȂ�B�Q���\�̏ꍇ�A�s�Ɨ�̌ŗL�l�i�����j����v����̂Łi�o�ΐ��j�A�s����s�Ɨ�̌ŗL�x�N�g����p���ĕ\�����邱�Ƃ��ł���B���ْl�����ƌ����邱�Ƃ������B
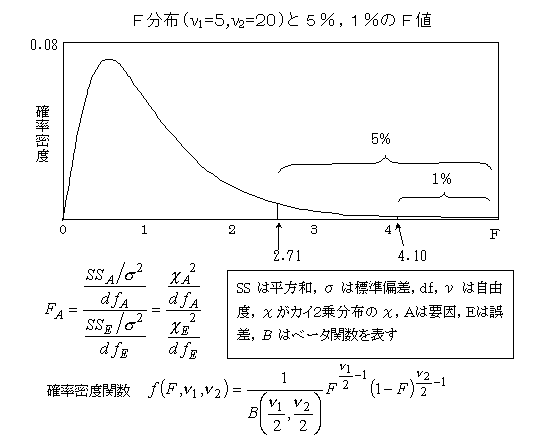
�e�\�E�e���z
���v�I��������̂Ƃ��ɗp����m�����z�D�Q�̓Ɨ�������2���z(�J�C�Q�敪�z�j������ϗʂ̔�̕��z���e���z�Ƃ��Ē�`�����D�����ɕ��U���͂̂Ƃ��̌���ɗp������D���U���͂ł́C����������i�K�ŁC�����_���ȕϓ��̑傫���i�덷�̕��U�j������悤�Ɍv�悵�C�ړI�Ƃ���v���̏����i�����j�̈Ⴂ�ɂ�镪�U���C�덷���U�Ɣ�r���āC���R�Ƃ͍l�����Ȃ����炢�傫���ꍇ�C�v���̌��ʂ��������ƌ��_����D���̏ꍇ�C�v���̕��U�̓J�C�Q�敪�z�����C�덷�̕��U���J�C�Q�敪�z������Ɖ���ł���̂ŁC�������đ傫�����r����D�J�C�Q�敪�z�̔�͂e���z����̂ŁC�e���z�̊m�������R�Ƃ͎v���Ȃ��قǒ������ꍇ�C�v�����ʂ����R�ł͂Ȃ��Ɣ��肷��D
�l�c�r�i�G���E�f�B�[�E�G�X�CMulti-dimensional scaling�j���������ړx�\���@�D
�`�g�o�i�G�[�E�G�b�`�E�s�[�C�K�w���́Canalytic hierarchical process�j
�������̗v�����K�w�I�ɑg�ݍ��킹�邱�Ƃɂ���āC�Ώۂ̎����[�e�B���e�B�[�𐄒肷����@�D�v���̐����̓��_�́C���ꂼ��d�v�x����Δ�r�ɂ���đ��肷�邱�Ƃ��s���Ă���D��Δ�r�̌��ʂ̕]��l�́C�{���Ƃ��đ��肳���D���������āC�t�̕]���͋t���ɂȂ�D�]��l��{���̑���l�Ɖ��߂��邱�Ƃ́A�`�g�o�̓����ł���B��Δ�r�̑���l�̏������@�ɂ́A�����̕]���҂̑I����������ړx�l�����߂�T�[�X�g���̕��@��u���b�h���[�̕��@�A�]��l�����̂܂܍��Ƃ���V�F�b�t�F�̕��@�A���E�ɐ��ʂ�z������P��a�@�Ȃǂ�����B�`�g�o�ł́C��Δ�r�ő��肳�ꂽ�s��̎听���i��P�ŗL�x�N�g���j��p���邪�C�P��a�@�̊��ςƓ������ʂɂȂ�D�����̗v����ʁX�ɑ��肷�邽�߂ɗv���Ԃ̑��֊W�������ł��Ȃ��̂ŁC����l�Ɍ덷����\��������D
�I�b�Y(odds)
�I�b�Y�́C�q���̓����闦�Ɠ�����Ȃ����Ƃ̔�iodds=p/(1-p))�ŕ\�킳���D������\�����P���傫�������������ŕ\���ł���̂ŁC���ۂ̏�ʂł͊m�������g���Ղ����Ƃ������D�ΐ����Ƃ������̂́C�ΐ��I�b�Y�i���W�b�g�j�ƌĂ�C�q���̏�ʂɌ��炸�C���ۂ̏o�����̎w�W�Ƃ��Ă悭�p������D�ΐ����Ƃ�̂́C�O����100%�̕t�߂��g�債�C��{�I�Ɍ��ۂɂ悭�K�����邩��p������̂ł��邪�C�o���x�������z������ꍇ�̎��R�ꐔ�i���K���z�̕��ϒl�̂悤�ȃp�����[�^�j�ƃ��W�b�g����v���邱�Ƃ���C�ΐ��I�b�Y�i���W�b�g�j�����ۂɂ悭�������Ƃ́C���̍����������Ă���Ǝv����D�i�ΐ��I�b�Y�Q�Ɓj
�I�b�Y��
�Q�̃I�b�Y�̔�D�I�b�Y���댯�x��\�킷�Ƃ���ƁC�Q�̊댯�x�̑��ΓI�ȑ傫����\�킷�D�I�b�Y��͕��ꂪ�C��Y�����ł���I�b�Y�̔�ł���C����ɑS�̂̓x����p�����i�o�������j���Ί댯�x�̊T�O���ʂɂ���D�ʏ�̊m���́C�N���蓾�邷�ׂĂ̎��ۂ̂����C���ɂ��Ă��鎖�ۂ̊����ɂ���Ă�\�����C�q������ꍇ�C������\����������Γq���āC�͂����\����������Γq���Ȃ��C�Ƃ����悤�ɍl����̂ŁC�͂����m���ɑ��ē�����m���̔���v�Z����C�P���傫����Γ�����̉\���������C�P��菬������͂����\���������Ȃ�C�g���₷���Ȃ�D���ۏ�C������m�����P�ɋ߂��Ȃ�ƁC���Ȃ�傫�ȓx���Ŋ|����̂ŁC�P�Ȃ�䗦�ł́C���̌X����\���ł��Ȃ��D�䗦�́C�S�̂̑傫���ɑ���Y������Ώۂ̑傫���̊����ł��邪�C�傫����ΐ��ϊ����邱�Ƃ��l�Ԃ̃C���[�W�ɗǂ������Ȃ�C�䗦�́C�S�̓x���̑ΐ��ƊY���x���̑ΐ��̍��ɂ���ĕ\���ł���D����ɁC������̗��Ƃ͂���̗����C���[�W�I�ɔ�r���邱�Ƃ́C������̑ΐ��\���i�S�̓x���Ƃ̑ΐ���̍��j�Ƃ͂���̑ΐ��\���̍����Ƃ�悢���ƂɂȂ�D�I�b�Y�̑ΐ����Ƃ����ΐ��I�b�Y�́C��L�̂悤�ȍs�����f���̕\���Ƃ��ė����ł���D���W�X�e�B�b�N���������悤�ȉ��߂��ł���D�ΐ��I�b�Y�́C�����̃��W�X�e�B�b�N���\���Ɉ�v���邱�ƂȂǁC���v�I�ɏd�v�ȊT�O�ƂȂ��Ă���D
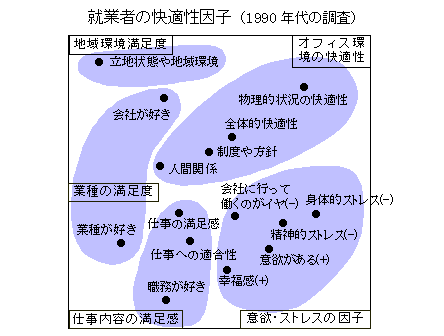
�I�t�B�X�̉��K�����q
�����ɂ���ăI�t�B�X�̃T���v����l�X�ȑ��ʂ���]���������ʂ���C�v���̃E�F�C�g�𐄒肵�Ă����C�v����ω��������Ƃ��̕]�����_�𐄒肷��Ƃ����I�t�B�X��]������V�~�����[�V�����V�X�e���D�l�Ԃ̕]���̎d���𐔗����f���ɂ���đ�p����̂ŁC��x�p�����[�^�i�E�F�C�g�j����͂��Ă����C�l�X�ȃI�t�B�X�ɂ��āA�V�~�����[�^�[���]�����邱�Ƃ��ł���D�uJ-16�I�t�B�X�̕]���V�~�����[�V�����V�X�e���v������D
Home�@���������@��ЊT�v�@�A�s�@�J�s�@�T�s�@�^�s�@�i�s�@�n�s�@�}�s�@���s�@���s�@���s�@�Q�l����