当社の業務で使用している用語を解説しています.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献
マーケットシェアの予測
新製品のシェア予測には、購入実験による予測(CLTレベル)、テストマーケティング、コンセプトテストと購入意向調査などがある.もっとも手軽なものとして、コンセプトテストがよく用いられる.コンセプトテストは、シェアの予測というよりは、コンセプトを提示することによるニーズの有無を調べることが目的とされる.アセッサーの項参照.
マインドシェアmind share
製品の嗜好度や製品の価値そのものから決まるシェア.マーケットシェアは,広告などによる製品の認知率awearnessや流通の支配力を含んだ市場カバー率distributionなどが重要であるが,マインドシェアは知名,ディストリビューションが100%のとき(製品の存在がすべて知られていて,買いたいときにいつでも買える状況)のマーケットシェアとも言える.製品の良し悪しや好き嫌いを表現しているので,マーケットシェアの最も基本的な要素である.逆に,既存の製品の販売量が分かっても,必ずしもマインドシェアが分かるわけではないので,予測のみならず,既存の製品についても,マインドシェアを測定しておくことは,販売量の原因を理解するためにも必要なことと言える.
マスコミ情報の分類(当社の報告書)
「E-001マスコミ情報のマップと関心傾向」はノンメトリックMDSと外部展開法の応用事例.データは20年近く前のものなので,現在の情報分類には使えない.外部展開法,ノンメトリックMDS,MDPREF分析など方法的に意味がある.
マハラノビスの距離Mahalanobis distance(多変量の距離)
相関の大きい変数を用いて距離を出すと、一つの情報を2重に使うことになるので、対象間の違いを正確に表現できない。極端な場合、相関が1の変数を使うと、同じ変数を2つ使って距離を計算することになる(あなたは男性ですか、あなたは女性ですかという質問を両方使うようなこと)。マハラノビスの距離は、互いに相関のある変数を用いたとき、その相関する部分を多重に使わないようにして計算する距離である。上記の「男性ですか」「女性ですか」という質問の場合、自動的に1つの変数にしてしまう距離である。相関係数が1ではない場合でも、その相関する部分を多重に使わないような計算をする。具体的には、主成分分析によって互いに独立した次元にして、分散(固有値)を1にし、もとの変数の方向に分配し、距離を計算する。変数の相関部分は、主成分の固有値の大きさに表現されるので、それを1にすることによって、多重性が除かれる。
多変量標準化(タ行の項目参照)は、多変量間の相関の多重性を除く計算操作であるが、下の計算式のように、マハラノビスの距離は、多変量標準化後のユークリッド距離になる。また、多変量正規分布は、多変量標準化後には独立した次元の正規分布として理解できる。
したがって、マハラノビスの距離の解釈は、見かけ上の相関を除いたときの距離(真の距離)を表現している。すなわち、マハラノビスの距離は、直交空間を求めないで、直交空間での距離を計算した場合にあたる。互いに相関する変数を用いるクラスター分析のときには、マハラノビスの距離が有効であるが、クラスターの重心を、もとの変数の平均値を用いて表現すると、重回帰分析の偏回帰係数の解釈と同じように、解釈できないことや誤って解釈すること(直交空間として解釈してしまうこと)がよく起こる。したがって、可能であるならば、変数間に本来的な相関関係がある場合には、直交因子などを求めて因子得点の類似関係を分析する(クラスター分析をする)ことが薦められる。
マルコフ予測Markov estimation
現状の状態を,単純集計値のように測定し,次期(1年後あるいは次回の購入など)への移行を測定し,1つの状態から他のすべての状態への推移率とする.1年毎の職業変化などは状態がはっきりしているので分かりやすい.すべての状態からの推移をマトリックスの形にすると,クロス集計表の横パーセント表のようになる.初期に測定された状態に,推移行列を掛けて,各状態を合計すると,1年後の状態が計算される.推定された1年後の状態に,さらに推移行列を掛けると,2年後の状態が推定できる.推移行列が長期間変わらないとすると,計算を繰り返すことによって数年後の状態を予測することができる.職業など時代によって人気に変化がある場合など,推移行列の要素に関数を入れることにより,外的な状況を加味することができる.職業などの予測事例,死亡者の予測事例などが,「E-106予測事例集にある」.新製品のマーケットシェア予測に利用されている.マルコフ連鎖参照.
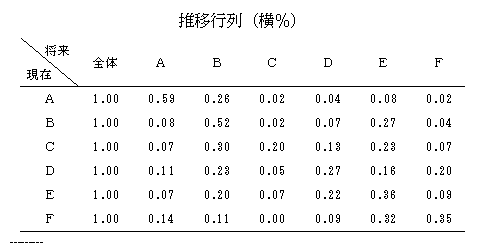
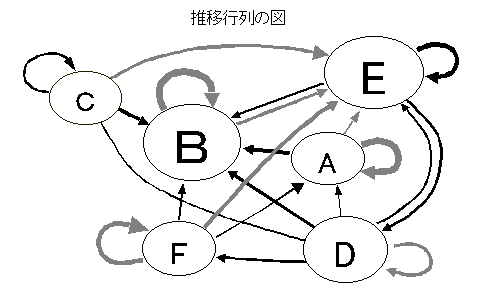
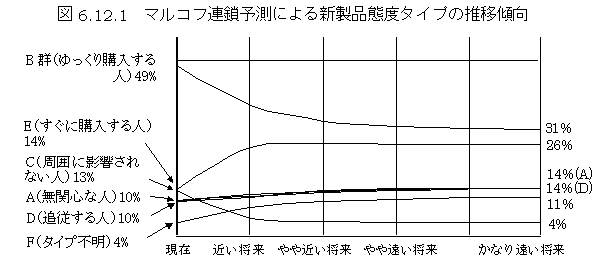
マルコフ連鎖Markov chain
当社では,消費者の購入,非購入の状況の変化を記述するために,用いられている.何らかの理由で,集合のメンバーが所属する集合を変える割合が一定であるとき,所属の変更をくり返すと一定の安定した状態に収束する.「A-08
マルコフ予測」,解説.「M-46 マルコフ予測」,プログラム.「B-02,B-03 マーケットシェア予測」(ASESSOR型予測)の中で利用されている.
マンテル・ヘンツェル検定Mantel-Haenszel test
2×2の分割表が層別要因ごとに測定されたとき,層別要因の影響を除いてから検定する方法.分割表をオッズ比(当たりはずれの相対比較値,危険度)として捉えるならば,層別要因の影響を除いた後のオッズ比(危険度)が1より大きいか否かを検定することを意味する.分割表の検定と言うよりもオッズ比または分割表自体を一つの統計量と考えて,超幾何分布または2項分布を想定し,分割表(独立した測定値はセルの1つの要素)の分布の期待値と全体の分布の期待値との差からカイ2乗分布を仮定した検定を行う.層別の分割表の分布に関する検定であるので自由度は1になる.超幾何分布を用いるので2×2以外の分割表に一般化することができる.また,層別要因に順序関係や数量的な調整変数が定義できるならば,その情報を使った方が(傾向検定)検出力は上がる.同じデータについて,オッズ比の対数をとれば(ロジット変換),尺度の上限下限がなくなり,正規分布を仮定した要因分析を適用することができ,層別要因や交互作用の検定に便利である.マンテル−ヘンツェル検定は「M-53統計的仮説検定」にプログラムがある.マンテルヘンツエルは層別要因(交絡要因)効果を除いたオッズ比の計算法を提案したので,その修正式をマンテルヘンツエルの修正式という用語が使われることがある.検定に関しては,コクランも提案しているので,コクランの名前も同時に用いられることがある.
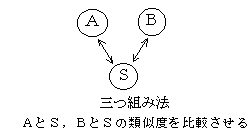
三ツ組法
刺激間の類似度を測定する方法.刺激の3つを組にして,1つの刺激が他の2つの刺激の類似度のどちらに近いかを判定させる方法.
無作為抽出(random sampling)
調査や実験など母数を推定するためには,正規分布の仮定や母集団からサンプルをランダムに抽出することが基本的な前提になる.
無相関検定
相関係数r=0の帰無仮説を検定する方法.t=rSQR(n−1)/SQR(1−r2) (df=n-2)のtテストが用いられる.
名義尺度nominal scale
カテゴリー変数の測定値.性別,職業などは,対象の特徴を表す一種の測定値でるが,数量的な意味,順序関係などがない測定値なので名義尺度値と言える.S.S.Stevensが,測定尺度を名義尺度,順序尺度,間隔尺度,比尺度に分類した.測定尺度レベル参照.
メジアンmedian
中央値.データの特徴を表す代表値の一つ.複数のデータを大小順に並べたとき順位が中央のデータの値.データの分布の山が1つのときには,上下のはずれ値に影響されない.代表値には,平均値やモードがある.
モード(最頻数)
ヒストグラムを作ったとき,度数が最も高い値を示した位置.分布の形を見たときに最も多くのデータが集中しているので,代表値として使われる.単純集計表の度数分布に対応している.データが少ない場合などでは階級(一つのヒストグラムの幅)の採り方によって結果が異なってしまう.山が2つ以上あったり,一様分布の形式をしている場合には,モードだけを見るとデータの特徴を見逃してしまう可能性がある.
モーメント(積率)
分布の特徴を表し,期待値(平均値)として定義される.平均からの2次のモーメントは,データの重心からデータの隔たりの2乗(2次)を平均したものであり,分布の広がりを表した分散になる.3次のモーメントは分布の歪み,4次のモーメントは分布の尖り(裾の広がり)を表す.正規分布の3次のモーメントは0,4次のモーメントは3になる.
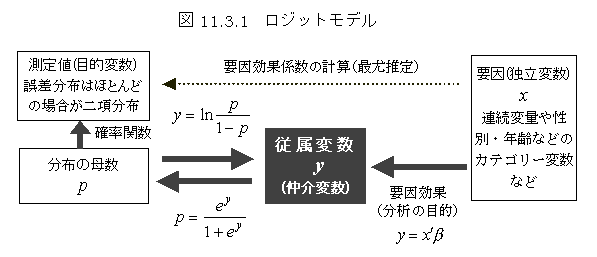
目的変数と説明変数
重回帰分析のような要因分析のとき、原因となる変数を説明変数、結果となる変数を目的変数と言うことがある。重回帰分析のとき、原因となる変数を独立変数、結果となる変数を従属変数と言うこともある。通常の重回帰分析の場合には、従属変数と目的変数は区別する必要がないが、ロジスティック回帰分析やポアソン回帰分析などの離散型の目的変数の場合、要因効果を受ける従属変数は、測定値としての目的変数と区別される。すなわち、ここでは、測定値を目的変数と言い、ロジットのような要因効果を受ける変数を従属変数と呼んでいる。従属変数は、潜在的な変数や分布の自然母数としての意味を持つ。
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献