当社の業務で使用している用語を解説しています.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献
パーセントポイント・ポイント(パーセントの差を表現するときに用いる)
パーセントは、全体を100としたときの部分の占める割合を表す単位であるが、パーセントの差を表現するときには、とくにパーセントポイントという単位を用いる。例えば、「20%が50パーセント増加」と言ったとき、20%が70%になる場合と、20%がその50%である10%増加して30%になる場合(変化率)の2つの事象を表現してしまうので、変化率を表す場合はパーセントで表現し、差を表す場合はポイントを付けて区別するという約束である.人数や個数などは5パーセント増加という場合と5ポイント増加という場合を使い分ければ誤解が生じない.パーセントを取り扱っていることが明白な場合には,単にポイントと言うこともある.
バイプロット表現
主成分分析の結果を2次元平面に表現した場合が,バイプロットと呼ばれることがある.
配本モデル(当社の販売量予測システム)
「J-01配本モデル」では,販売要因を①販売形式要因,②営業要因,③社会経済要因,④季節要因,⑤地域特性要因,⑥内容要因と地域との交互作用要因の6つに分け,すべての要因効果を同時に解かないで,優先順位を決めて順次,予測パラメータを計算する方法をとっている.各要因は,販売量に作用する心理的,行動的なレベルが異なっているので,必然的に優先順位が決まる.要因間の相関は,優先順位の高いものに含まれることになる.「E-106予測事例集」,「C-005重回帰予測の適用例」に収録.
パスシミュレーション(パスモデルによるシミュレーション予測)
パスモデルを用いて、情報の量を推定し、予測する方法。パス係数は、変数間の関係の大きさを表すが、個々の対象の変化が情報の変化にどれほど大きな効果を持つかは別の問題になる.すなわち、パスが大きくても、そのパスを利用しない刺激があったり、パスはそれほど大きくなくでも、めいっぱい情報を通過させるような刺激もある.その違いは、刺激の持つ尺度値の大きさに起因する.実際にパスを通過する情報量(効果量)を推定してみると、最終目的に作用する要因はそれほど多くないことが分かる.複雑な因果の効果を有効に生かすためには,中間的な変数が仮説構成体以上の実在に近いほど安定したものにする必要がある.広告効果、学力、満足度など、中間の変数の安定性が結果の有効性に重要な要因になる.
パス分析pass analysis
因果関係を表したパスモデルのパラメータを推定し、パスモデルを作ること.条件を統制してパス係数の統計的な有意性を検証することは、変数間に関連性がみられるか否かを調べることを意味する.このような検証は,人間の内的な仕組みを調べるためには重要であるが,最終的な目的変数を規定する度合いを予測するすること目的にすると,たとえ統計的に有意であっても,様々な要因が存在する現実場面では,目的変数への寄与は,ほとんど誤差と区別できなくなるほど小さいものになってしまう.操作を目的にした場合には,単に有意かどうかだけでなく,かなり大きな効果が見出されなければ,操作コストなどを設定することが難しい.予測のためには、比較的小数の要因を確実に把握することが重要になる.
花のイメージ評価
イメージ測定法を「花」に適用した場合.結果は、プロフィール(レーダーチャートなどの表現)、嗜好度、イメージマップなどの形に表現される。「J-17イメージ測定法」参照。
判断judgment
人間の行動を感覚(インプット)、知覚(中枢での受容)、認知(意味づけ)、反応(アウトプット)というレベルで分けるとき、その反応のレベルを、心理的な状態から、反応の形式であるカテゴリーや数量、言語などの表現法への変換の部分について、とくに判断という概念を用いることがある.判断機能が結果を左右するので、その機能の研究が重要である。
判別型AID分析
AID分析の目的変数を判別群にした場合の分析法(多群でも構わない).CAIDは,同じように目的変数がカテゴリーであるが,目的変数にランダム誤差成分を想定して,適合度をカイ2乗値などにする.判別型AIDは,目的変数として,群を表わすダミー変数を用い,分析結果の最終的な群は,目的変数の群に一致する.すなわち,群を分ける要因を探す方法といえる.分析結果は,要因の数が十分あれば確実に100%分類できるが,分類するパターンが必ずしも一つではないので,最も単純な形が出力されることになる.(2004.4)
判別分析discriminate analysis
判別分析は、群を予測する統計的方法であり、2群の判別(重回帰分析と同じ計算法になる判別分析)、多群の判別(判別関数法=確率的な確からしさの関数)、尺度化の多群の判別(正準相関分析と同じ計算法になる判別分析)、予測変数がカテゴリーである場合の多重判別(数量化2類)などがある。2群の判別分析は、1次元尺度上に2群の得点分布を想定して、特定の判別点を境にして、2群を予測する.解き方は,2群に得点を与えてそれを従属変数にして予測変数のウェイトを最小2乗法によって求める.判別得点の単位を調整すると、2値の重回帰分析と同じ結果になる.判別関数法は、群ごとに確率密度関数(多変量正規分布など)を想定して、ある対象の各群に属するときの確からしさの得点を求めて、群を判別する方法である。多重判別分析は、多群を判別する方法であるが、各群と説明変数との関係が独立していないので、因果関係の主成分(正準因子)を求める方法である。いわば群と説明変数との対応関係(距離ではなく相関=構造ベクトルを用いる)を求めて、説明変数から計算されるサンプル得点(正準因子得点)の位置によって群を判定する。数量化2類も多重判別分析と同様に正準因子を求めてウェイトを定める.数量化2類も多重判別分析も正準相関分析と同じ計算法になるが、数量化2類の場合は、説明変数項目のカテゴリーの処理が特徴的である(数量化3類や1類と同じ処理法)。
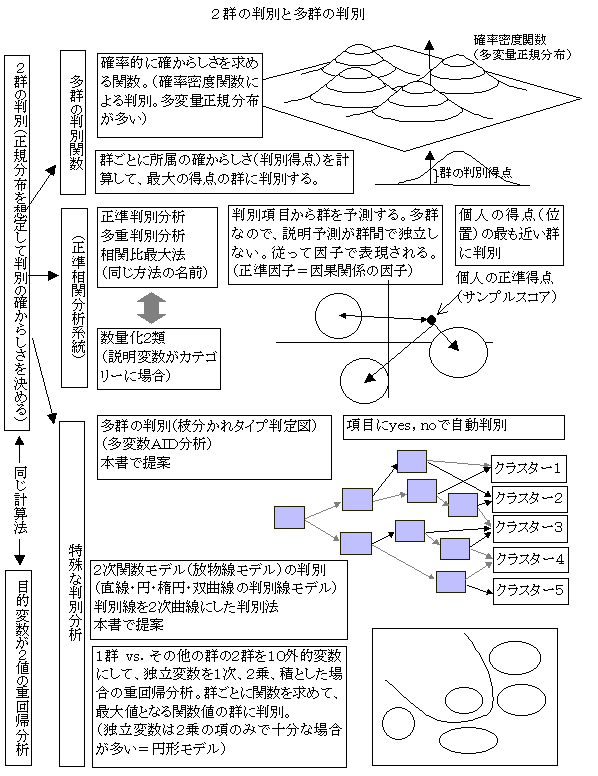
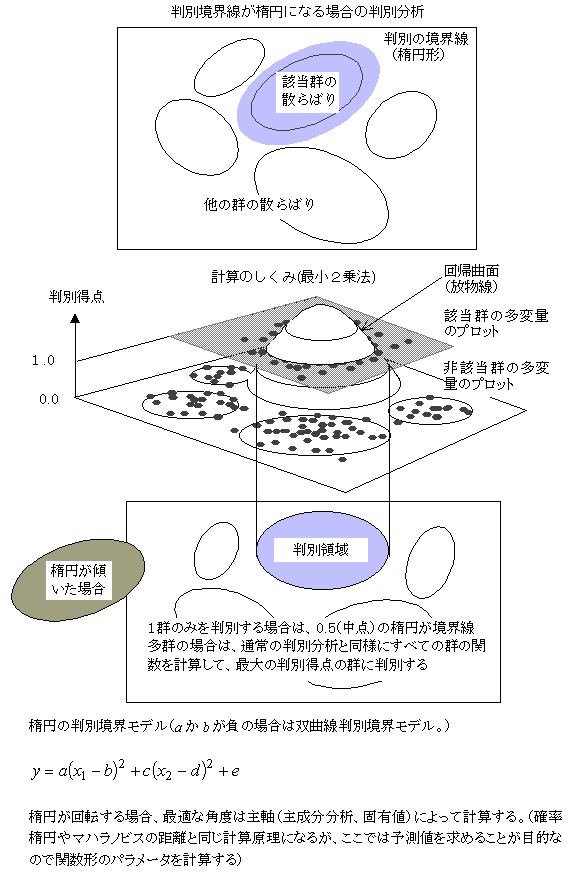
判別分析(判別境界が楕円になる場合)
重回帰計算の2群の判別を発展させると、判別境界を楕円にすることができる。楕円(2次関数)は、最適値を表現できるので、周囲に他の群がある場合についても最小2乗法によって多群の判別関数を求めることができる。判別方法は、群の数だけ2次の判別関数を計算し、判別したい対象の判別得点を群の数だけ計算して、最も大きな得点を持つ群に判別すればよい(確率分布を想定した判別関数法と同じ判別方法)。楕円が傾く場合は固有値計算が必要なので(主成分分析、主軸計算)、多変量正規分布の場合(判別関数法)と同じくらいの計算手数になるが、双曲線も表現できるの判別精度は高くなると思われる。空間が区別されていない場合は、どのような方法を用いても判別精度は上がらないので、本質的な精度(計算法に依存しない精度)は、測定変数の問題になる。
判別分析とロジスティック回帰分析・ポアソン回帰分析などとの関係
通常のデータでは,目的や習慣によって使い分けに迷うことはないが,原理的には,被説明変数が01型(該当,非該当)の形式になるので,適用に迷うことがある.判別分析や数量化2類,などは,01データそのものが被説明変数になる.ロジスティック回帰分析などにおいては,理論的な目的変数は,ロジット(対数オッズ)などの要因ごと(集計されたデータ)に想定される比率などの統計的パラメータ(母数)になる.
判別分析では,決まった群が目的変数になるので,目的変数はランダム変動をしない.したがって,説明変数の影響力を見る場合,説明変数の方が誤差を伴う測定値に当たるの、2群差のt検定などが指標になる.分散分析や重回帰分析においては,目的変数が測定値であるので,t検定が説明変数ごとの目的変数の差になるのと逆の関係になっている.
ロジスティック回帰分析などでは,01のデータにランダム変動(測定誤差)が含まれていると考えるので,分散分析などの要因分析に当たるので回帰分析になる.01データのランダム変動(誤差変動)には,データに即して,二項分布,ポアソン分布,ワイブル分布(指数分布)などがあるので,データに合わせて分析法を選択する必要が出てくる.
ただし,ランダム変動として,二項分布(該当,非該当が一定の母集団から比較的多くのサンプルを抽出した場合)が適用できたとしても,比率に対して正規分布を仮定する(プロビットモデル)場合もあるし,ロジスティック分布(ロジスティック回帰分析)を仮定しても,少数データに適用させるために,測定値に正確な直接確率計算(超幾何分布など)を想定するようなモデルも成り立つので,ランダム変動の捕らえ方によって多数のモデルが考えられる.
判別分析は,目的変数は確率変動するのではなく,判別のための群であるので,説明変数が偏らなければ,典型的で安定して群を用いた方が判別には都合がよい.ロジスティック回帰分析などでは,自然な(ランダムな)データである必要があるので,典型例のみを用いると,その結果の利用が限定される.判別関数の利用の面白さは,明確な事例を用いると良い判別ができるという点にある.
汎用分散分析プログラム(当社のカテゴリー重回帰分析のプログラム)
繰り返しが不揃いの場合,要因が直交しない場合,交互作用がある場合、数量化1類、コーホート分析、メトリックコンジョイント分析、連続変量を予測変数に含んだ場合、共分散分析法、正準相関分析、多変量分散分析、数量化2類などは、カテゴリカル変数の01コーディングとウェイト計算(カテゴリーウェイト)の手順を付随させると、一つの分析プログラムで解くことができる。単調回帰法の手順を組み込むとすべてノンメトリック法として解くこともできる。ただし、要因が直交しない場合など、データ数が少ないと、必ずしも、妥当な推定値が得られるとは限らないので、測定の方法が最も重要な問題になるのであり、解法の汎用性と信頼性とは別の問題である。
ビー・アイ・ビー・ディー BIBD(balanced incomplete block design)
釣合型不完備ブロック計画.官能検査などの例では,多数の刺激があるときには,すべての刺激を一度に評価することができない.その場合,刺激をいくつかに分けて別の日に評価をする.各実験日はブロックと言える.各ブロック内で全部の評価をしないのであるが,2つの刺激が同時に評価されることを会合というが,全体として各刺激の会合数が等しい場合釣り合っていると言う.すべての刺激がいっぺんにランダム化された形で評価されることを完備型(乱塊法)というので,上記の例はバランスのとれた不完備型のブロック計画BIBDと言われる.刺激が多数ある場合には,完備型の実験ができないだけでなく,実験回数が多くなるためにバランスのとれた実験をすることもできない場合が多い.その場合には,会合数が不均衡になることを許した部分的釣合型不完備計画(PBIBD)になる.ブロックと刺激や評価者に偏りがなく,特別な交互作用が予想されない場合には,ブロック内の順序,評価者の順序,刺激の無作為化などによってバランスがとれていなくても実験を実施することが多い.
ピー・エス・エム PSM(price sensitivity measurement)→プライス・センシティビティ・メージャーメント
ピー・オー・ヴイモデル POVモデルpoint of view
個人差を考慮した多変量解析.Tucker & Messick(1963)が提案した3元データの多変量解析法.始めに個人空間を構成し,個人空間内の特定の点(point of view)における刺激空間を分析する.3相因子分析の前段階の分析と言える.「A-31 POVモデル」が解説書.「E-002企業イメージ」や「E-012知能テスト」が応用例.
非階層クラスター分析→「K-MEAN法」参照.
比較判断の法則comparative judgment law
サーストンの比較判断の法則は,刺激が心理尺度上で正規分布をすると仮定して,比較判断結果を2つの刺激の差の分布から推定することを提案した.すなわち,比較判断結果の割合を正規分布の割合として,z得点を求めて尺度値とする.比率を推定するのであるから多くの回答が必要となる.応用ではほとんど使われることがない.間隔尺度値を求める恒常法と同じ考え方になっている.
比の差の検定
検定をする場合,比率はいくつかの種類に分けられる.①一つの質問についての回答者の割合の差,②同一回答者の質問間の差は対応のある比の差の検定,③性別などの個体の群間の比率の差は,通常のカイ2乗検定,などになる.①の回答カテゴリーの差は,度数が小さい場合は2項確率,度数が大きい場合はカイ2乗検定か正規分布の確率,②と③は計算法が異なるがカイ2乗検定を利用する.
微分方程式モデルと人間の行動
例えば,車などの移動距離を考えるとき,特定の位置(出発点)を原点にして,時間と移動した距離のグラフに表現できる.微分係数は,特定の位置での速度にあたる.通常,人間の感覚で,移動距離を計算する場合,「この速度でこの位の時間を走ったから,この辺まで来たかな」というように考える.すなわち,感覚的に理解できるのは,速度や加速度であり,距離は計算することになる.このような状況を記述するためには,速度や加速度の法則性を第1義的に考えることになる.速度の法則性は,微分方程式に対応し,距離の計算は積分に対応する.一般に,人間の感覚は,相対的な変化のみを理解して,記憶による第2義的に座標値を理解するのが普通であるので,微分の法則性(常微分方程式など)を見つけることが自然である.方角に関しても,現時点の変化のみ(極座標の角度の微分)を基準にして考えることが行われる.最終的には,変化ではなく,座標値(エネルギーレベルの座標値)を求めなければ,操作や予測ができないので,通常の関数形を定める(微分方程式を解くことが対応)ことが必要になってくる.
標準得点(standardized score)
測定値を平均値を原点(0),標準偏差を尺度値の単位に変換したした得点.マイナス得点が平均値より低いことを表わす.テスト得点などを標準得点で表現すると,もとの得点の意味がなくなって,平均からの偏差を表わす相対的な値になる.例えば,身長と体重は単位が違うので,数量的には比較する意味がないが,「太っている」とか「痩せている」などと言うときには,「身長は平均的であるが,体重は平均より大きい」などのように,人間のイメージでは身長と体重を比較している.このような人間の機能を表現するためには,「標準得点の比較」はかなり有効な数量的記述モデルであると言える.標準得点はz得点ともいう.「z得点」,「基準化」参照.
表情とその印象についての分析(当社の研究課題と報告書)
表情や人間の顔を再現するとき、部分の物理的な要素のみによるのではなく、多数の印象評価の01コーディングからデータベースを利用した再現法がある。その場合、評価項目は、やさしさ、色の印象、目の大きさ印象、髪の印象、丸さの印象、太り具合、出身国の印象、~のような感じ、と言うようなものになり、それらの再現は多くの評価データベースから平均的に選ばれる.データベースが少ない場合には、平均することができないので実在する特定のひとが選ばれてしまう可能性が出てくる.
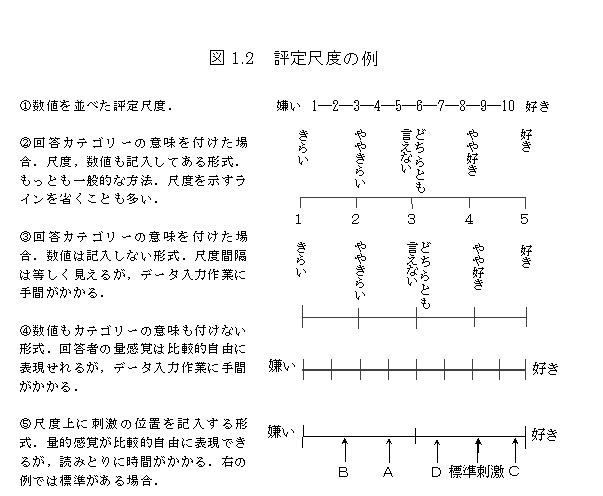
評定尺度法
評価対象にものさしのような数直線を当てて、得点化する方法.数直線を当てないで程度を表す言葉による評価をする場合もある.好き嫌いの評価について例に取れば、もっとも多く用いられている手続きは、かなり好き、好き、やや好き,どちらとも言えない、やや嫌い,嫌い,かなり嫌い,という言葉を評価対象に当てはめるようなものである.多くの場合,そのまま数値を与えて,平均したり多変量解析を適用したりする.評定尺度法には、数直線に直接評価対象の位置を記入したり、数値を答えたり,いくつかのパターンがある.シェッフェの一対比較法では、比較結果を評定法で測定して間隔尺度値として分析する.サティのAHPでは、評定尺度値を比率や倍数値して数値を当てはめて、原点に意味を与えて分析する.
ファジー分析
重回帰分析(A-55)の中で取り扱われているファジー重回帰分析で用いられている用語.ファジー分析では,あいまいさを表現するために回帰係数自体を一定にしないで,幅をもった値として表現する.係数が一定である現象が確率分布をするという通常の分析とは現象を記述するモデルが異なっている.解析的には,正規分布を用いないことなど、かなり簡略的に取り扱えるので多くの現象を記述するのに便利であるが,人間を取り扱う場合、なぜファジー関数を適用してよいのかというような現象のプロセスを記述するモデルがまだ不明確である.偏回帰係数にファジー数を適用する場合,三角型関数によって回答のあいまいさを係数に反映させると下の図のようになる.
フェヒナーの対数法則(Fechner's law)
物理量と心理量との関数関係(心理物理関数)が対数関数になるという考え方。多くの場合、よくあてはまる。心理物理関数は対数関数かベキ関数になる。対数関数は、マイナスがない現実の数値を実数全体に広がる数値に変換し、指数型分布などを含めた一般的な変換方式の原理となる。フェヒナーは弁別閾(差異が分かる刺激の幅)を連続させることから対数関数を考えたが、より一般的には、任意の基準点からの変化率(一般的ウェーバー比)を連続させることから導くことができる(印東他、1977参照)。重量刺激について、恒常法的な実験によって、大きな範囲での多くの勾配を求めてみると(代、1975未発表資料)、対数関数がよく当てはまるが、刺激の大きな部分の勾配は、対数関数より曲線的に変化する傾向があるので、パラメーターの多いベキ関数の方が当てはまりはよい。
不動産物件価格計算(当社の計算システム)→中古不動産物件価格計算.
負の2項分布とポアソン回帰モデル(対数線形モデル)
データ入力作業のようにミスが比較的少ない作業でのミスの出現は,ポアソン分布をすることが予想されるが,多くの作業員をコミにして取り扱ったとき,間違いやすい人と比較的間違いの少ない人がいるために,負の2項分布の方が良く当てはまる.これは,ポアソン分布のように,期待値(λ)を一定であると仮定することに無理があり,期待値にも大小に変化する分布(ガンマ分布)を想定する方が現象に良く合うためである.この例では,負の2項分布はポアソン分布のパラメータ(λ)が個人によって変動する(確率変数)ことを想定し,全体のデータの分布を表現した場合になる.同様に,ポアソン分布のパラメータが,要因によって変動すると考える場合に,ポアソン回帰モデルがある(対数線形モデル).ポアソン回帰モデルは,負の2項分布とは異なって,パラメータ(ポアソン分布の自然母数(LN(λ))が,要因によって線形的に左右されるとして,その要因効果の大きさを推定し,出現率を予測しようとする考え方である.ポアソン回帰モデルは,潜在的な目的変数(パラメータの変動)について,必ずしもガンマ分布を想定しているわけではないが,ガンマ分布がカイ2乗分布の一般形であることからも分るように,変動係数が小さい場合やNが比較的大きくて分布が対称であることが予想されるときには,対数正規分布を想定しても大きな問題にならないから,両者は,関連性の深い現象記述モデルと言える.
部分相関係数(part correlation coefficient)と一般化特異値分解
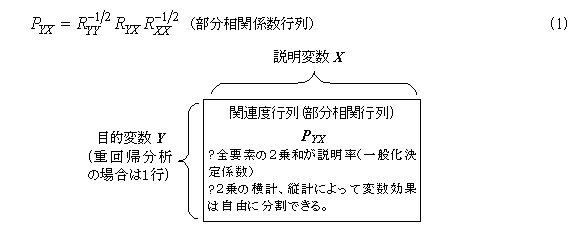
部分相関係数は、重回帰係数(決定係数)や正準相関係数(一般化決定係数)を構成する個々の説明変数の寄与を表す指標である。すなわち、各変数の部分相関係数の2乗を合計すると決定係数や一般化決定係数になる。偏相関係数が独自の寄与を表しているのに対して、部分相関係数は、独自の寄与も含めた寄与全体を表している。したがって、部分相関行列の2乗の行和、列和、あるいは任意に加算すると、要因効果を自由に分解することができる。
計算の原理は、(1)式のように、目的変数と説明変数間の相関係数に目的変数と説明変数それぞれの逆行列の平方根行列を左右から掛ける。正準相関分析や多変量分散分析、数量化2類などの多変量の部分相関係数の2乗は、互いに相関を持つ変量を、直交成分に分解し、全体の分散を固有値の合計ではなく、1に基準化し、各変数の分散の受け持つ割合を表している。すなわち、変数レベルの分散(固有値の大きさ)ではなく、独立した次元での分散を全体の分散にしているので、同じような意味の変数(相関の高い変数)を調整している多変量の分析法と言える。多変量の要因分析では、直交成分は主成分軸に限定されず、要因空間全体としての寄与が問題となるので、もとの変数に寄与が戻されてその大きさが表現される。(部分相関行列)
(1)式の形から分かるように、部分相関行列は、一般化特異値分解で取り扱われる行列と同じである。したがって、正準相関分析や多変量分散分析は、部分相関行列の主成分分析と言える。また、コレスポンデンス分析と同じように、部分相関行列は、目的変数と説明変数の主効果を除いた関連行列を表しているので、多変量の標準化操作に当たり、得られた得点行列の内積は分散に当たる。したがって、平方根行列の変換は得点の変換になり、2乗に当たる逆行列や射影子による変換は分散のレベル(ベクトル)での変換になる。
重回帰分析の場合の部分相関は、1行のベクトルになる。
部分的線形性
人間行動に線形モデルを当てはめると、部分的には当てはまりがよいが、広範囲にみるとほとんど当てはまらない.逆に言うと、適当な範囲を限ると、線形モデルが当てはまる場合が多い.演算の簡単さを考えれば、応用上は、適用範囲を限った線形モデルがもっとも実用性が高い.
ブラッドレイ・テリー・リュースの一対比較モデル(Bradley-Terry-Luce model
for paired comparison)
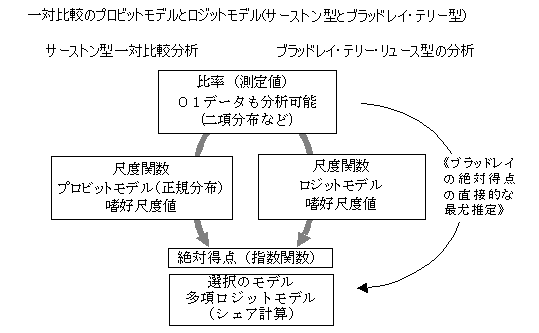
ブラッドレイ・テリーの一対比較モデルは、選択割合(勝率)が、選択肢全体の得点合計に対する選択対象の持つ得点の割合になると考えるモデルであり(下の式)、得られた比率から得点(プラスの値)を推定することに視点がある。リーグ戦の勝敗から強さの尺度値などを求める事例がよく取り上げられる。この考え方は、嗜好度(強さ)を、持っている玉の個数に例えれると、対戦相手の持っている玉の個数と自分の個数の合計に対する自分の個数の割合が勝率になると考える。勝敗から玉の個数を推定することが目的になる。下の式から分かるように、測定値は左辺の比率で、右辺の未知数を求めることになる。比率が割り算になっているので、非線形の式の推定になり、最尤推定法が用いられるが、反復近似法の計算法が、ブラッドレイによって示されている(「官能検査ハンドブック」など参照)。
上記の玉の個数は、比率の測定値を個数レベルで表現したもので、測定値のレベルの得点になっている。要因分析や強さの変化を取り扱うときには(選手の補強やファンの数などの要因分析)、プラスのみの得点(いわば自然数)は非線形のモデルになるので取り扱うことが難しく、一般的には、強さ(嗜好)の尺度を潜在的な尺度として別に定義することが行われている(離散型選択モデル、ロジスティック回帰分析、プロビットモデルなど)。上記の玉のモデルから分かるように、二項分布-ロジットモデルを適用することによって、強さの尺度(効用値)を定義することができる。
ロジットは、比率の対数であるが、結局、度数(勝ち数)の対数変換とその差に帰着できる(君山、2004など参照)。したがって、自然界の測定値と人間の要因効果イメージとを結びつけるモデルとしての指数関数・対数関数モデル(心理物理関数の基本モデル)に帰着し(Luce、1958など参照)、ブラッドレイ・テリー・リュースモデルと言われている(下の式参照)。この考え方からすると、強さの得点(嗜好得点、効用値)は、足し算,引き算が自由に定義できる実数尺度上の値になり、要因効果についての分析も行うことができる。
また、ブラッドレイ・テリーモデルは、選択行動の極値分布(常に最大値を選択することによる確率分布)としてのガンベル分布(指数型分布をする対象の最大値の分布、2重指数分布)から導かれる多項ロジットモデルとしても取り扱うことができる(Luceモデルと同じ形になる)。以上のことから、ブラッドレイ・テリーの比較モデルの分析結果は、ブラッドレイのπではなく、効用値のレベルで計算されて、利用されることが多い。
これに関連して、サーストンの一対比較法は、正規分布を適用したプロビットモデルと言える。ブラッドレイ・テリー・リュースモデルもサーストンモデルも、回答(測定値)に相関関係(相互作用など)がない場合を前提にしているが、相互作用がある場合の分析法として、サーストンではモデル1,2,3,4(相互作用がない場合はモデル5)などがあり、リュースモデルでは、Tverskeyモデル、多項ロジット関係では、入れ子型多項ロジットモデルや主成分分析モデル、一般的な極値モデル(多くの具体的なモデルがある)などが取り扱われている。

ブランドイメージbrand image
製品のジャンルによって評価項目が異なるが,当社の評価では共通したイメージ評価項目を使うことによって,他の種類のイメージ評価を比較できるようにしている.(動物と花,色,都市,国,人物などをそのまま比較できる)
フロペンシティスコアpropensity score
測定さてた(調査された)値にサンプリングによる歪みがある場合や欠測値missing dataがある場合、基準となる複数の変数(性、年齢、職業、居住地などの属性など)から、プロペンシティスコアを計算しておいて、スコアの近いものを用いて補足したり、スコア計算のウェイトを用いて集計値を修正したりする。集計値の場合、基準変数が性,年齢、地域、特定の商品の所有率など、単純な場合は、ウェイトバック集計が用いられるが、交互作用を無視したリムウェイティングの方法が用いられることとがある。プロペンシティスコア法は、これらの方法を一般的にしたものと理解できる。基準変数が複雑であったり、インターネット調査のように、通常のサンプリングをしない場合など、基準変数が規定できるならば、修正をした方が実体に近いと言われている。一般にはウェイト付けが不可能な場合にも適用することができる。欠測値の補足やマッチングの技法としては、ロジットモデルや対数線形モデルが用いられる場合があり、欠測値の最小2乗推定を一般的にした場合と言える。予測変数には、交互作用を含めたり、多次元のプロペンシティスコアを考えることもできる。
分散分析法analysis of variance
平均値の差が偶然かどうかを判定する統計的検定法.例えば,測定値の性別の差が偶然かどうかを調べたいとき,測定値の個人得点の分散と,性差の分散(性別の平均値の差をもとにして計算される)を比較して,性差の分散が偶然と思われる程度より大きかった場合,性差の分散は偶然ではなく,したがって,分散のもとである性別の平均値間に差があると考える.分散についての分析であるから,分散分析と言われる.一般に,偶然かどうかの確率は5%か1%が用いられ,F分布の確率を利用する.F分布などを仮定する場合には,データが目的要因以外はランダムに選ばれていることや正規分布などの前提条件があるが,一般には,とくに偏った測定がなされていない場合,前提が満たされていると考えて検定を進めることが多い.調査データなどでは,評定尺度法など,前提条件が厳密に満たされていない可能性があるが,特に系統的な偏りが予想できない場合には,分散分析などの検定をすることが多いので,応用するときにも,測定データに即した使い方をする必要がある.
当社の分散分析システムは,要因が直交しない場合には,多重表の平均値を用いたり,重回帰分析のように安全な(消極的な)検定法を用いている(直交しない場合,要因の分散の合計は全体の分散より小さくなる).交互作用は7要因まで分析できるが,一般には,データが多くないので,2要因,3要因くらいまでの交互作用しか明確には解釈できない.実際の現象においても,交互作用があるのか,主効果の質的違いなのか,判断できないことが多い.
文章意味集計(用語検索)システム
文章で書かれたデータから,出現する単語,文節を集計するシステム.集計したい内容(意味)とそれに対応する用語(具体的な出現語)の対応表を前もって作成するので,異なった表現を持っているが同じ意味の使い方を集計できる反面,同じ表現で異なった意味の用語を同一語として集計することになる.文章を読んで意味が理解できる場合には,そのような意味が理解できるような文章を意味対応表に入れる必要がある.行動予測のためには,言葉の意味を読みとると言うより,限定された状況の中で,仮説的なモデル構造のどの部分を表現しているかを明らかにすればよいので,利用状況を限定するとそれほど大きな誤解をすることはないと思われる.たとえば,文章から企業の好き嫌いを調べたいときには,使われている言葉は,好きを表現していることなのか嫌いを表現していることなのか,ということが分かればよいので比較的誤差が少なく判定できると思われる.数量化する場合にはウェイトが付けられる.ウェイトは01の場合もあるし,1,0,-1の場合や複雑なウェイトを想定する場合がある.このように,行動の予測に関して重要な次元や枠組みを想定して,出現する言葉を集計すればよい.メッセージ性の大きい言葉は,単語に限らず,文節,文章,記号,音声があれば抑揚,高低,大きさ,質など様々な要素がある.これらの要素を,目的に合わせた仮説体系の中に位置付ける方法が文章意味集計システムになる.集計するための具体的な作業は,仮説意味空間を想定すること,仮説意味空間と現象としての言葉をつなぐ翻訳辞書を作ること,などが最も基本になり最も重要なことである.調査と集計作業では,文章を区切って入力するかしないか,離れた単語を組み合わせるか否か,漢字とかな,漢字の送りがな,など様々な問題がある.実際の作業結果から見ると,およそ80~85%程度自動検索ができる.意味仮説を単純化すれば検出力は上がるが,どちらにしても厳密さを必要とすると最終的には人間の判断に頼らざるをえない.データがデジタル化できると様々な統計分析が可能である.コンコーダンス参照。「M-30」が分析システムであり,「J-03」が解説書.現在ウィンドウズ化されていない.翻訳辞書は限られたものしかない.
ペアワイズ法pair-wise method
要因効果の測定法.トレードオフ法とも言われる.提示される2つの刺激を対比較しながら,刺激全体を順序付ける.ほとんど,機械的に実施できるように手続きが構成されている.おもに、コンジョイント分析の測定のときに用いられる方法であるが、一対比較の状況は,サーストンの一対比較法や感覚測定法の恒常法と同じようにどちらかを選択する形式になる.サーストンの一対比較法や恒常法、ペアワイズ法などは、その分析法が異なっている.当社には,エクセルVBAによる測定プログラムが用意されている.分析法は,ノンメトリック重回帰分析を用いている.
平均値表のコレスポンデンス分析→コレスポンデンス分析(平均値表)
平均の差の検定
2つの平均値の差の検定には,t検定を用いる.母分散が分かっている場合には,正規分布の確率,2つの分散が異なっている場合には,ウェルチの方法を用いる.同一人の2つの測定値の差には対応のある場合の検定.複数の平均の一様性検定には1要因の分散分析を適用し,平均間の対比較にはテューキー・クレーマー法やフィッシャーのLSDなどを用いる.多重比較検定の項目参照.分布に偏りがある場合や得点に上限,下限がある場合には,変数変換が考えられるが,変数変換をする場合には,形式的に変換するだけでなく,できるだけ,正規分布の尺度値の意味が分かるようにした方がモデル構成や演繹的応用のためには有効である.オッズ比,ロジスティック関数,学習曲線,対数関数などは比較的心理的な解釈が可能な変換になっている.
ベキ関数power function
y=axn (a,nは定数).行動の記述としては,xを物理測定値,yを心理量としたとき,ベキ関数が当てはまるとしたベキ法則がある.実験状況によって対数関数よりもあてはまりが良い場合が多い.ベキ関数は,ベキ指数というパラメータ(母数)を持つので,対数関数に近い状況も記述できる(0<n<1
の場合).ベキ関数の曲率がなめらかに変化することが,対数関数よりも現象に当てはまることの理由と思われる.しかし,対数関数は,指数関数の逆関数であり,演算上は極めて便利であるので,ベキ関数よりよく利用されている.
ベクトルモデルvector model
外部展開法の表現法の一つ.嗜好の傾向を刺激空間内の方向で表す.ベクトルは,回帰平面の傾きの方向を示している.
ヘドニック法hedonic pricing method
主に環境の評価法として利用されている。複数の要因のうち、一つのみ欠けた場合(あるいは異なった場合)の評価値をコスト(金額)に換算して測定する。マンションの価格について、他の条件を一定にして、駅からの距離のみを変えたときの価格の差を測定するような場合である。この方法は、重回帰分析の偏回帰係数を直接測定することに当たり、要因を統制したときの1要因実験に対応する。価格が要因の単価として利用できることは分かりやすいが、価格が価値と単純な1次関係にない場合には、適用の範囲を限定するか、金額を適当に変換する必要がある。要因間に交互作用がある場合や少ない測定値によって多くの要因効果を測定すると、通常の多要因実験やコンジョイント分析に似てくる。回答を価格ではなく相対比較を系統的にすると、ジョンソンのACA測定法に近くなるが、ヘドニック法の特徴は、要因を絞ることと要因効果を価格で表すことにある.
偏差値
数量的な測定値は,原点(ゼロ点)と単位によって表現される.異なったテストの得点などを比較する場合,すべてに共通したゼロ点と単位が決められないとき,そのテストの相対的な得点によって表現することが有効なことが多い.基準点を平均値とし,単位を標準偏差にし場合が,標準得点(z得点)になる(z=(x-m)/s(mは平均,sは標準偏差).この尺度値は,平均0,分散が1になるので,分りやすいが,さらに,得点を,2桁のプラスの整数で表現するためにZ=(x-m)/s×10+50(mは平均,sは標準偏差)の式で変換することが行われている.この変換値が偏差値と言われる.平均が50,分散が10になるように作ったので,30点以下が2%,40点以下が16%,50点以下が50%,60点以下が64%,70点以下が84%になる.尺度値は,使い慣れて実際上の問題と直接結びつくと,理解しやすくなるのであるが,偏差値は,学力の評価の方法として広く使われるようになったので,リアルで分りやすい数値として用いられている.
弁別閾difference limen
ある基準となる刺激に対して違いが理解される刺激値.弁別閾より基準刺激に近い刺激は,区別できないことが多いが,時によって違いが理解されることがあるので,刺激は人間にとって統制できない要因によって連続体(心理尺度)上でばらついていると仮定されている.したがって,弁別閾を測定するときには,刺激が正規分布していると仮定して,多数の測定値によって分布の形(平均と分散)を推定して,操作的に弁別閾を定義することが行われている.ほとんどの場合に区別できない,という条件で弁別閾を定義すれば,弁別閾は基準刺激に近くなり,半数程度区別できる場合によって定義すると,弁別閾は基準刺激から遠くなる.弁別閾は一人の被験者について定義できるのと同様に,同じ定義の仕方が集団についても適用できる.集団の場合には,ほとんどの人に区別できない弁別閾,半数の人に区別できる弁別閾というような意味になる.
変量模型→母数模型.
ホールカウントアナリシスhole count analysis(データ入力作業など)
データのカラムの数字をカウントする方法.データが保存されている状態をそのまま表現し,単純集計などの操作は含まない.データ入力や加工のエラーチェックに用いられる.もともと,パンチカードの穴の数を数えることからこの名前がある.「M-01 集計システム」 集計システムの一部になっているが,データの確認用にいろいろと利用される.
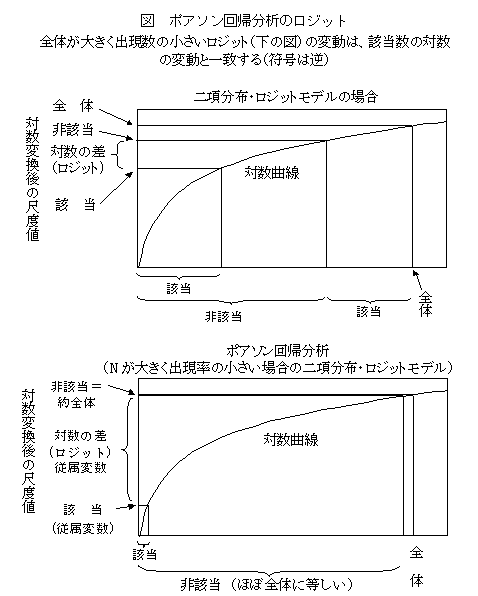
ポアソン回帰分析(対数線形モデル)
集計度数の要因分析をする方法.ポアソン回帰分析は,該当者数が小さい場合の集計データの要因分析に適用されることが多い.該当者数と非該当者数の両方に測定値が関係する場合には,ロジスティック回帰分析が適している.ポアソン回帰分析は,非該当者数と全体を区別する必要のない場合に当てはまる.ポアソン分布が指数分布の仲間であるので,その自然母数が比率の対数変換値によって表現されることから一般に対数線形モデルと呼ばれることもある.測定度数の分布にポアソン分布を仮定することから,パラメータの推定には,最尤法が用いられる.
ポアソン回帰分析(対数線形モデル)は、ロジットの特殊な場合と言えるが、自然現象では、対数モデルの方が、一般的で自然なモデルで、ロジットの方が特殊な現象と思える。
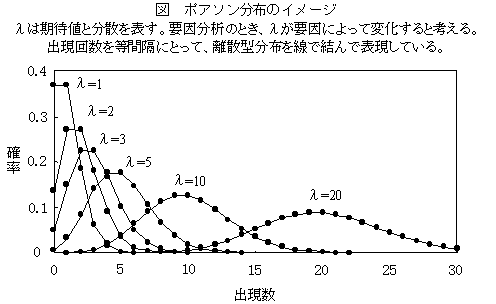
ポアソン分布Poisson distribution
2項分布において,出現確率が小さく,測定を多数回行ったときに出現度数の分布(np=λでn→∞).指数分布族の離散型分布.2項分布があてはまるような壺の中の赤玉(少ない)と白玉(多い)の例のとき,割合が極端に偏っている場合に、多数試行のときの赤玉の当たる個数は,ポアソン分布をする.一定期間での事故や死亡など,出現率の小さい事象の起こる回数,出現率の小さい疾病などに当てはまる(稀現象).工場などの間違い行動は稀現象であるが、事象が独立ではなく間違いやすい人と間違いにくい人がいるので,間違いを起こす人の分布としてガンマ分布を想定した場合のポアソン分布関数である負の2項分布(ポリア・エッゲンベルガーの分布)が,ポアソン分布よりよく当てはまると言われている.

ポイント(パーセントの差の表現)→パーセントポイント・ポイント
飽和モデルsaturated model
対数線形モデルやロジットモデルなどのとき,自由度が0になり,モデルが飽和状態になっている.いわば誤差が0になり,パラメータは連立方程式を解く形になる.より少数のパラメータを持ち,有効なモデルを探すとき,飽和モデルにおける対数尤度とモデルの対数尤度を比較することによってそのモデルの当てはまりの良さを判断することがある.
また,上記の意味とは別に,飽和モデルと言うときには,現象が単調増加傾向であり,飽和状態が想定されるモデル(漸近線があるモデル)を指す.行動を記述する場合には,学習曲線,ロジスティック関数などがよく利用される.上限を持つ成長曲線と言える.学習曲線,ロジスティック曲線参照.
母集団population
調査を行うとき,目的である集団をさす.例えば,支持政党を調べたいときには,条件がない限り,選挙の有権者全体を意味する.調査を行うとき,全数調査ができないので,サンプリングして結果を検討することになる.サンプリングするときの母集団のことである.
母数模型と変量模型(fixed-effect model , random-effect model)
分散分析の要因について、設定された条件自体が母数であるとき、その要因は母数模型であるといい、特定の母集団からの抽出であるときには変量模型という。人間の測定値のとき、個人差は母集団からの抽出されたサンプルになるので変量模型になるが,一般的な個人差ではなく,テスターとしての評価者の差異のみに興味がある場合には母数模型になる。特定の教授法の条件差などは、教授法一般の中から抽出されるのではなく、目的の教授法の違いをみたいのであるから母数模型になる。変量模型はサンプリング誤差があり、母数模型にはサンプリング誤差はないので、測定値の誤差分散の意味が違うので検定法が異なる。分散分析の要因に両方が含まれている場合には,混合模型といわれる.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献