当社の業務で使用している用語を解説しています.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献
内的整合性
一般に内的整合性というときには,問題としていることがらの内容は別として,内的な矛盾がないことを表す.数学的には,公理の正しいか否かは別にして演繹が正しくなされていれば内的整合性は保たれる.科学的研究においては,内的整合性が保たれていることが手続き上重要であり,技術的に正しいことを意味する.研究の内容が有用かどうかを議論するとき,内的整合性に問題がある場合,議論する前提がゆらいでいることになって,不毛な議論になる可能性がある.内的整合性は,研究の信頼性のことであり,定義の正しさは妥当性のことを意味する.
内部分析(internal analysis)
既に得られている分析結果に対して,その分析の構造の中に別のデータを位置づけることを外部分析というが,外部分析に対して,同一のデータのみから構造を求める分析法を内部分析という.→外部分析と内部分析
2項分布(binominal distribution)
壺の中に赤玉と白玉が入っているとき,1回ずつランダムに取り出して戻しながらN回繰り返したとき(ベルヌーイ試行)に,赤玉の出る回数は2項分布になる.N個をいっぺんに取り出したときには,超幾何分布になるが,市場調査のように母集団が大きい場合,いっぺんに取り出した場合であってもほとんど二項分布と同じになる.また,サンプル数が大きい場合には正規分布で近似できる.玉が3種類であれば3項分布になる.2項分布の確率は,ある製品の「好き」「嫌い」の割合の検定,改良後の「良くなった」「わからない」の割合の検定などに用いられたり,製品の不良の割合を抜き取り検査で推定したりするときに用いられる.超幾何分布,ポアソン分布など参照.
実際に,赤玉が1回だけ取り出すことがどれくらいの確率になるのかは,もともと,どのくらいの割合で赤と白が入っていたのかということと,何回取り出したのか,という2つのことが分らなければ,計算できない.すなわち,2項分布とは,玉を1つずつ,戻しながらランダムに取り出すことのプロセスを表現したモデルであり,試行回数と割合は,具体的な分布を固定するために必要なことである.このような,具体的な分布の位置などを決めるために必要な定数をパラメータ(母数)という.
2項分布は,出現回数が度数でカウントされるので,離散分布である.赤玉が出る回数をx回(変数)とすると,赤玉の出る可能性(含まれている割合)pをx回引きあてる割合と,残りの試行回数(n-x)が白玉である可能性(1-p),特定の玉を取り出し組み合わせ(nCx)によって表現できる.分布の確率密度関数は,y=nCx・px(1-p)n-x.調査の場合では,nはサンプル数であり,pは回答率に当たる.何回か繰り返した場合,同じ母集団であっても測定された回答率が,図のように分布することが予想される.(2003.3)
2項分布の自然母数
2項分布の確率は,2つの母数(pとn)を持つが,その特徴は,ポアソン分布,正規分布,指数分布などと共通した点があり,指数型分布ファミリーの1つである.指数型分布の標準形で表現すると,y=exp〔xlog{p/(1-p)}+nlog(1-p)+lognCx〕 (対数は自然対数,Cは組み合わせの記号)のようになる.この式のlog{p/(1-p)}は,指数部分の中で変数xと掛け算になっており(線形関数の係数の形),xとは独立に変化する数値であり,自然母数と言われる.xに独立であることは,分布のの内側の性質には左右されないので,外側の要因との関係を見るためには適当な数値と言える.ロシスティック回帰分析の場合では,比率の変動について,その要因効果を分析するのであるが,目的変数として,ロジットlog{p/(1-p)}が用いられる.測定値が2項分布をする場合,ロジット(潜在変数)が自然母数に一致することは,2項分布(指数型分布族)と現象とが深く関連していることを示している.しかし,潜在変数上の得点分布と,測定の状況とは本来,無関係なものとして考えられるので,測定された比率pと潜在変数とを直接結びつける考え方(モデル)は,もっと自由に規定できると思われる.ロジスティック回帰分析,一般化線形モデルなど参照.(2003.3)
二重打ちの照合(データ入力)
データを入力したときのエラーチェック.別の人に,それぞれデータを入力させて,後で照合し,一致したところで入力データを完成したことにする.2人が同時にエラーをおかす可能性は,入力するデータやエラーの出やすい数字,入力した人の個人的くせなどによって異なるが,以下のように考えられる.100個の数字入力を必要とする調査3000サンプルのデータがあるとき,全部で3000×100=300,000字の入力数になる.入力担当者が5サンプル入力するごとに1箇所間違えるとすると,その人は100×5=500字に1回間違えることになり,全部で3000/500=600箇所の間違いを入力することになる.その人と同じ間違い率の人が別に入力したとすると,2人とも同時に間違える可能性は500×500=250,000字に1箇所くらい間違っている可能性がある.回答者の勘違いなどのチェックをしたり,記入ミスをチェックすることにより,通常,二重打ち後の間違いが,問題になることはほとんどないほど小さくなる.
2重重心変換(2重中心化)double centering
距離行列を表現するとき、相対的な位置関係が意味を持つ場合、行平均、列平均、全体平均を用いて原点にして表現し、距離を原点からのベクトルの終点間距離と考えると、距離行列はベクトルの内積によって表現できる(ヤング-ハウスホウルダーの変換)。そのほか、重心を原点にして表現すると、便利なことが多い。もともと意味のある原点による座標であるときには、計算後、もとの原点による座標に戻す必要がある。測定値自体が距離であるときや(MDS分析など)、コレスポンデンス分析のように、相対的な関係を表現したいときでは、重心変換する前の解は、原点までの次元が含まれるので、見かけ上の値が出力されるので、それを除くためには重心変換した後の方が有効な解釈ができる。
ニュートン法・ニュートン-ラフソン法
方程式の解法.方程式が解析的に解けないときなど,数値的に解く方法.数値的に解くとは,数値を代入しながら近似的な解を求め,応用上十分な精度の解を近似的に求める.ニュートン法は,適当な初期値を与え,微分係数(接線の傾き)に表現される直線によって近似解(直線とy=0の交点)を求め,その解の値の微分係数によって次の近似解を求める,という反復計算によって徐々に真の解に近づける.ニュートン・ラフソン法は変数が複数の場合のニュートン法であり,連立方程式を解く形になる.データ分析では,最尤法によるパラメータの推定のとき,指数型分布族の対数尤度関数の最大値を求めるときによく使われる.最大値は,接線の傾きが0の場合になるので,偏微分して0とおいた連立方程式を解くことになる.微分して0となる場合は最大値に限らず,最小値,変曲点などがあるが,指数型分布族の場合には最大値を求めることができる.最尤法の解き方には,このほかフィッシャーのスコア法などもあるほか,最大値を解く数値的解法は,多くあるが,試行錯誤的なので計算時間が比較的掛かる.できるだけ解析的要素を含んだニュートン法などの方法が計算時間が短い.
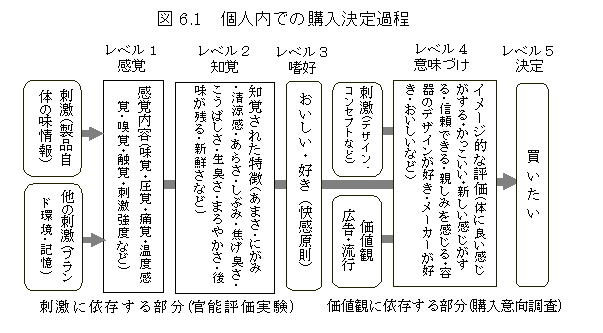
人間の判断機能モデル
感覚情報や製品情報などの受容,刺激の差異による知覚過程,記憶や個人的な欲求,習慣,価値観などによる刺激の個人的位置づけ,購入条件による購入行動や評価結果の表示,というように人間の行動を規定する部分によって異なった構造をしている.基本的に線形モデルで記述するにしても,変化しにくいものと変化しやすいもの,すべての人間にほとんど共通しているしくみ,集団的に固定しているもの(国民性や世代性など),集団的であるが規定しにくいもの(好みや考え方),個人的な変動,などの違いを考慮しながら,予測モデルを構成しなくてはならない.判断機能のモデルは,人間の共通した機能であるが,刺激の理解(誤差分散と心理的な数量化)と表出時の特性(心理的な数量の言語化と行動化)に視点を置いた方法論的な部分を取り扱っている.
ぬき取り検査(sampling inspection)
品質管理の方法.製品の中からランダムに一定の数のサンプルをぬき出して,不良製品の割合を調べる.統計的には2項分布やポアソン分布を当てはめて,全体の不良率を推定することができる.
ネーミングシステム
無意味語や通常のイメージ評価をするシステム.花,動物,有名人,などと同一の空間に表すことができる.「J-17イメージ測定法」参照.
年代効果(コーホート分析参照)
世代効果と同じ.年代は生まれよりも生育課程を強調した表現法になっている.コーホート分析のときに時代(調査した年の特徴),年齢と区別して,その世代要因を想定する.時代要因は流行現象,価値観の変化(流行の一種)などとして捉えられるが,世代要因は,純粋には,同じ環境によって成長したことにより,一生変化しない特徴を表すが,実際には,世代の特徴が共通して変化した場合には(世代と時代の交互作用)世代効果として抽出されることになる.
年齢変化(コーホート分析参照)
調査などによって得られるような現象としての年齢差には,世代の違いが含まれているが,純粋の年齢変化の要因は,一人の個人が一定の年齢に達したときに起こる変化を意味する.その変化を多くの人について共通した要因として捉えることが多くのコーホート分析の課題になっている.時代によって変化傾向が異なれば,時代と年齢の交互作用があることになる.
ノンパラメトリック検定(nonparametric test)
ノンパラメトリックとは,統計的仮説検定を行うとき,母集団の正規分布やそれに付随する分布を前提にしないような検定法を意味する.ノンパラメトリックの直接の意味はパラメーターを用いないことであり必ずしも分布を仮定しないことを意味していない.具体的には,測定値に正規分布の仮定ができない場合や分散の等質性が保証できないときなど,t検定やF検定が使えないので,ノンパラメトリック検定を行う.測定値自体には正規性やパラメーターに関する前提が満たされないが,検定にはカイ2乗分布の確率を利用することが多い.当社では,計算の依頼によってプログラムを開発しているが,2項確率検定,多項確率検定,直接確率法(超幾何分布),マンテル・ヘンツェル検定,コクラン・アーミテッジの傾向検定,スティール・ドワスの多重比較などが多く使われている.
ノンメトリック(non-metric)
ノンメトリック(non-metric)とは,測定値が順序尺度として与えられているときに用いる.これに対して,メトリック(metric)は連続量(間隔尺度以上の測定値)で与えられている場合を意味するが,メトリックの場合には,メトリックの用語を付け加えないのが普通.通常の分析法がメトリックな分析法であるので,測定が順序情報の場合の分析法も,メトリックな分析法と同じだけあることになる.メトリックな分析法では,量的な大小間の差異を分析情報として使うために,少数のはずれた値や分布に偏りがある場合など、結果を見る人のイメージとかけ離れた次元や誤差を抽出することがある.このようなときノンメトリックな方法を用いると,次元が小さくなり,人間のイメージによく合う結果を出力することができる。測定の尺度レベルの問題のほか,計量的に測定されていたとしても、比較的次元数を小さく(計量的な分析の寄与の小さい次元を吸収する)したいときには、ノンメトリックな方法が有効であり、応用しやすい結果を得ることができる。ノンメトリックカテゴリカル重回帰分析法,ノンメトリック重回帰分析,ノンメトリックコーホート分析法,ノンメトリック数量化1類,ノンメトリックパス分析法,ノンメトリック分散分析法などの方法も想定できる。
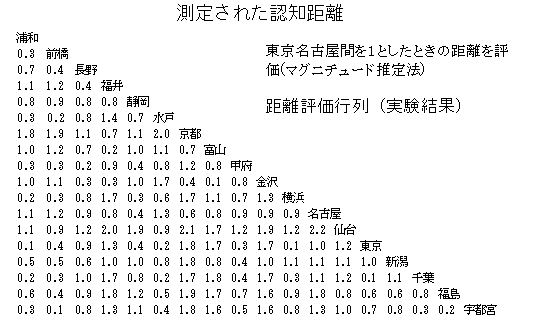
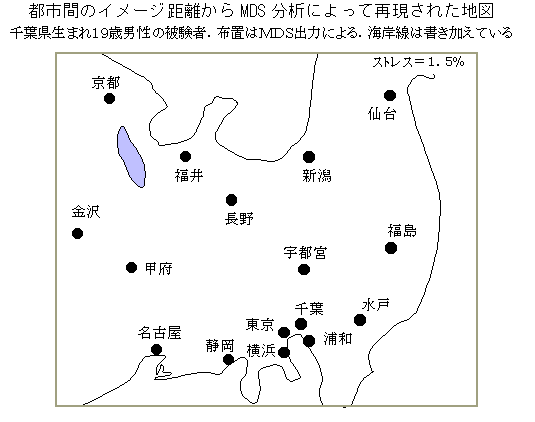
ノンメトリックMDS(非計量的多次元尺度構成法)non-metric multi-dimensional
scaling
MDSは刺激間の距離行列や類似度行列から空間的な座標値を推定する方法である.MDSの考え方によると,もともと刺激は空間的に位置付けられており,そのことが元になって,現象としての刺激の類似関係が得られると考える.すなわち,顔の似ている度合や見間違い,音の聞き違いの度合,製品の代替関係,競合関係などは,互いに近い位置関係にあるために起こると考える.空間的な位置関係が前もって分かっているときには,上記の現象を予測することができるが,データとして,現象の類似関係のみしか無い場合,あるいは空間次元がはっきりと分からない場合には,刺激相互の類似関係から空間布置を推定することになる.このことから,競合関係,類似性の原因などを明らかにすることができる.メトリックMDSは,距離行列から空間布置を推定する方法であるが(多次元尺度構成法の項参照),ノンメトリックMDSは,データの類似関係の順序情報のみを用いて空間布置を推定する方法である.心理的な類似度の評価結果は,正確な距離にならないことが多いので,広く利用されている.分析方法は,初期値としての空間布置を決め,そこから距離行列を計算する.その距離行列とデータの類似度行列とから単調回帰法(順序情報の処理法)によって,当てはまりの良さのストレスを求める.ストレスに関して各未知数に対する勾配を求め(偏微分),座標値を勾配方向に適当な幅だけ移動する(最急降下法).その後,単調回帰法,ストレス計算,勾配,座標値修正を繰り返して,座標値が変化しなくなったら終了する.最急降下法は,最小値を求めるとき勾配のみから最適値を探すので,極小値がある場合,最小値に到達しない可能性がある.したがって,初期値として,最終結果に近い布置を与えて,ノンメトリックMDSは最後の調整のために利用すると妥当な解が得られる.一般的には,欠測値がなければメトリックMDSが良く,欠測値がある場合には,類似度行列から2次的な距離行列を計算してメトリックMDSを用いると,ほとんど極小値に収束しないようである.
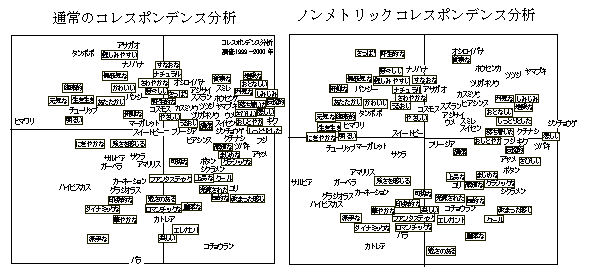
ノンメトリックコレスポンデンス分析non-metric correspondence analysis
コレスポンデンス分析は、行と列とが異なった要素の場合のマッピング法と言えるが、座標値を求める場合に特異値分解を用いている。同じモデルについて、順序情報のみを使ったノンメトリックMDSによって解くことができる。通常のコレスポンデンス分析を適用できるデータに、ノンメトリック法を適用すると、一般的に、数値の大小感がなくなる結果になるので(順序が同じであれば、大きな数値はより小さく、小さな数値はより大きくなりように使われるので)、分析結果は、①空間に均等にばらつく傾向を持つ、②計量的な多次元は、2次元空間に矛盾が少なく納まる傾向がある、などの特徴が見られる。通常のコレスポンデンス分析よりも、対数コレスポンデンス分析に近い。2次元マップ上で、だいたいの位置関係を知りたいときには、コレスポンデンス分析の3次元以上の説明不足についての不安がかなり解消される。
この分析法は、ノンメトリックMDSを用いた展開法モデルの解と同じである。
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献