
当社の業務で使用している用語を解説しています.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献
ライフスタイル測定法(当社の項目集)
「B-15ライフスタイル測定法」は調査項目集.内容は,パーソナリティ,価値観,購入態度などであるが,実際に応用する人は,そのまま使うことがほとんどなく,調査ごとに異なった項目を付加したり,用語を改めることが多い.したがって,その都度,因子分析とクラスター分析を使ってタイプ分けすることになり,一般的な傾向を把握できない.
ラウンドロビンround
robin
一般に、評価対象が均等に扱われる状況を表す。特に総当たり戦を表すことがある。調査などで製品テストを行うときには、多数の製品のうち、1人の評価者が2つの製品を単独に評価することと、その2つの対象の比較評価(どっちがどれだけ好きかというような評価)をさせることが一般的である。評価対象が4つの例では、2つを取り出す組み合わせは、6通りあるので、6つのパネルを設定して、それぞれ、2つの製品を評価させる。食品のように順序が重要な時には、逆順があるので、12通りの評価者の群が必要である。各20人のパネルの時、240人の評価者が必要になる。1人が1つを評価する場合よりは評価者が少なくてすむ。一人が3つ以上評価する場合には、順序効果を取り除くために、かえって評価者の人数を多くしなければならなくなる場合もある。
分析方法について、製品の単一評価の部分は、順序効果などが均等になっているので、通常の1要因の分散分析と多重比較などによって製品の差異をみる。より検出力を高める(微妙な差異を検出する)には、順序効果、組み合わせ効果などを考慮した分散分析を適用することができる。一対比較データの部分は、カテゴリー評価の時にはシェッフェ型の分散分析と多重比較が可能である。比較が、好きな方を選択するというような場合には、データが比率になるので、ブラットレイ-テリー型のロジスティック要因分析やサーストン型のプロビット分析によって製品の尺度値が計算できる。
ランダム効用モデル(random utility model)
競合するいくつかの製品など場合,効用値の大小によって選択されると考えられるが,例え効用値が測定できたにしても,複数の人のデータを取り扱うと,単純に,全体として測定された効用値の大小によって選択行動を表現することができない.効用値の差が極端な場合とほとんど差がない場合には選択される割合が異なってくる.このような現象を効用関数によって表現する場合もあるが,特定の対象の効用値にランダム変動要素を考慮して,分布すると考えると,効用値の差異の大きさと選択行動の関係がうまく説明できる場合がある.このような効用値のランダム変動(考慮できない要因,個人差変動など)を想定した選択行動の考え方がランダム効用モデルと言われる.選択肢に最大値の分布であるガンベル分布を想定すると,形式的に選択の割合がシェアの計算と同じようになり,2者選択のロジットモデルを一般化した形になることから,ガンベル分布のパラメータについて,ロジスティック回帰分析と同じように要因分析モデルを導入したモデルが多項ロジットモデルと呼ばれる.
ランダムサンプリング(random sampling)→無作為抽出.
乱塊法(randomized block method)
実験目的である測定を同一の条件下で行うことが難しいときに,実験をブロック化して,ブロック内で一通りの測定を行う方法を乱塊法という.ブロック間の実験条件が幾分異なったとしても,すべての測定対象が等しくその効果を受けるので,偏った結果にならない.実験の制御はブロック内で厳密に行い,別のブロックではそのブロックとして厳密に制御するというように,局所的な制御が重要である.官能検査の場合のように刺激の数が多くなったり,刺激の管理が難しくなると,完備型の実験計画のみならず,乱塊法実験(完備型実験)もできないことが多い.そのような場合には,ブロック間で測定のバランスをとる釣合型不完備ブロック計画BIBDを実施するが,それも実現できないときには,ブロック要因(測定日など)が均一になるように,できるだけ釣り合うように工夫した計画を立てざるを得ない(一部釣合型不完備ブロック計画).
乱数
出現の順序に特定の傾向を持たない数字の並び.出現の度数が一定の区間で同じである場合すなわち,分布が矩形分布をする乱数の場合を一様乱数という.出現分布が正規分布をする場合には正規乱数という.一様乱数から正規乱数を作ることができる.自然界では制御できない要因が一つの現象に作用している場合ランダムな測定値が得られる.乱数サイコロ(形が精密に作られているサイコロ),カードのシャッフルなどによって作ることができる.コンピュータで,乱数並びの数列を作ることができるが,同じ計算を行うと繰り返して同じ並びの数列を出力するので,初期値に乱数に近い数値を入力しなければならない.乱数を利用するとき,乱数並びの数表が用意されている(乱数表).乱数表はいつも同じなので,コンピュータの場合と同様に出発点をサイコロやカードなどでランダムに決めれば乱数並びを得ることができる.調査をするとき,母集団の対象の並びが要因についてランダムであるならば,3つおき,4つおきなど系統的に抽出したとしても乱数によって抽出した場合と同じにランダム抽出になる
離散型選択モデル(desclete choice model),質的選択モデル
商品,環境要因,個人的価値対象物などの効用値(ユーティリティ)の測定結果が,離散的(カテゴリー選択肢)である場合に,その選択を規定する要因効果を記述するモデル.競合する商品の選択行動(取引銀行の選択,お茶の選択,観光地の選択など多くの適用例が報告されている)のシェアについての要因分析(属性,特徴,価格など)などはこのモデルを適用することができる.
選択行動を記述する効用関数モデルとしては,量的に測定された効用値の要因を分析する線形モデル(重回帰分析など)から,質的に測定される選択肢の分析に発展したと言える.分析データの形は,数量化2類,判別分析と同じになるが,これらの方法は,目的変数に確率変動を想定しない判別の問題として捉えるが,一般的な離散型選択モデルは,目的変数に確率変動を想定しているので,重回帰分析のような要因分析になる.
心理測定法の立場から言うと,カテゴリー反応の分析に当たり,その他の測定法としては,順序反応を測定する場合,効用値をそのまま測定したり,一対比較法で測定したりすることはある.
統計的要因分析法の立場から見ると,判別分析,数量化2類(正準相関分析,多変量分散分析系統)から,2値反応のロジスティック回帰モデル(離散的目的変数の重回帰分析)やポアソン回帰モデル(対数線形モデル)が使い分けられるようになったことから,このようなロジットモデル(対数正規モデル,プロビットモデル他のある)がそのまま,離散型選択モデルの解法に用いられる.3つ以上のカテゴリーに関しての要因分析法については,効用値の変量(潜在変量)にガンベル分布(2重指数分布,第1種の極値分布,最大値分布)を想定することによって,形式的な矛盾が解決される,多項ロジットモデル,反応カテゴリー間に独立性が想定できない場合の入れ子式多項ロジットモデルnested
logit model(線形モデルではないので代入した下位の項が入れ子型になる),相関するカテゴリーと相関しないカテゴリーを定義する一般化極値モデル(generalized
extreme value model,GEV)などが利用される.幾つかの専門的なソフトウェアが開発され購入することができる.実際のデータを分析してみると,カテゴリーが少ない場合には,利用できるが,カテゴリーが多い場合(10カテゴリーなど)は,対数正規モデルを想定したり,連続変量に効用値を測定して,分散分析的な操作を行うことが比較的応用目的に沿った結果を出すことができる.いずれにしても,効用値の確率分布や反応の確率変動などを直接確かめるような方向のデータが必要である.(2003.4.23)
理想イメージ分析
消費者が望んでいる製品イメージ(コンセプト)を測定する方法.基本的には2つの方法がある.1つは多くの製品属性について,重要視する点を質問し,同じ属性について既存の製品を評価して,同一空間内に既存製品,理想製品を表現する方法(直接測定する方法).2つめの方法は,既存の製品についてその嗜好度を測定して,ブランドマップの中に最も好まれる位置を求める方法(間接的に測定する方法).後者の間接法には,ブランドのマップの中に理想点を求める方法と,コンセプトイメージ(意味空間)内に理想点を求める方法の2つの方法がある.(2002.2.14)

理想点モデル
外部展開法のモデルの一つ.刺激空間内に最も好まれる点を求める方法.外部展開法参照.
リッカート法
尺度構成法.反応が正規分布をするという仮定をもとにして,刺激の尺度値を求める.刺激が課題である場合には,刺激の尺度値は課題の難しさを表す.課題の回答者がその問題をクリアすればその課題の尺度値を与えられる(LIS知能尺度など).尺度化の対象が回答カテゴリーであれば,カテゴリーに与えられる尺度値によってカテゴリーの間隔が定義される.
類似度データ・類似性データ(similarity data)
刺激感の距離データから刺激の座標値を推定するのが,メトリックMDSであるが,メトリックMDSの分析対象である距離データを測定することは難しい.そこで,比較的回答しやすいデータとして刺激感の類似関係を測定した結果を分析できるノンメトリックMDSが1960年代に開発された.似ている度合いを評価するのに「似ている」「やや似ている」とか「AはBよりCに似ている」というようなレベルの測定値からでも分析できる.また,混同率,代替率などのデータも分析することができる.このような,類似関係を表したデータを類似度データ,類似性データと呼んでいる.通常の距離データであっても,ノンメトリック法の分析が可能であり,次元の縮小やだいたいの位置づけを知りたいときにはメトリック法よりノンメトリック法の方が有効なことが多い.ノンメトリックMDS参照.
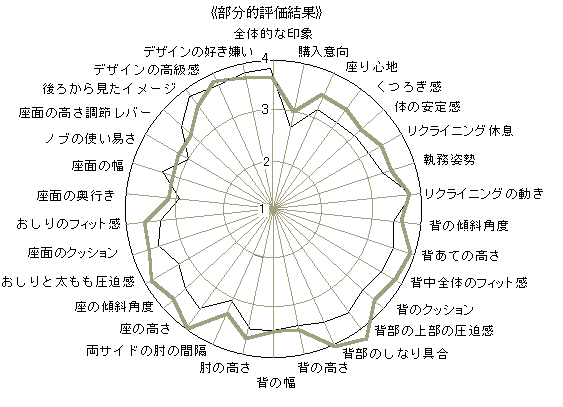
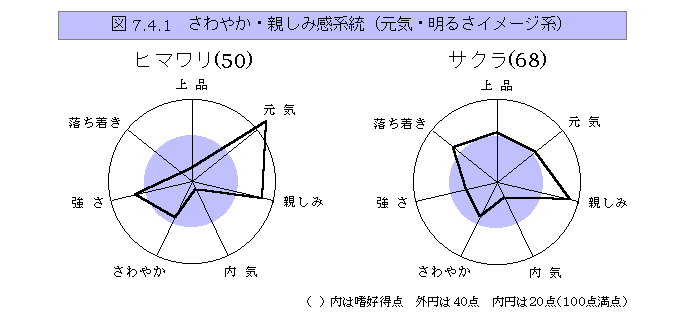
レーダーチャート(radar)
グラフ表現法.放射状に軸を設定して多次元の傾向を表現する.尺度値を結ぶと,くもの巣状の図形になり,多次元の特徴を良く表現できる.20~30の多数の尺度の場合でも用いることができて,特徴の把握に便利である.ただし,尺度の順序を換えると異なった印象になったり,尺度の目盛の採り方によって異なった印象をつくるので,やや恣意性がある.折れ線グラフの方が恣意性は少ないが,レーダーチャートの方が特徴の把握にすぐれている.
レンジ(range,範囲)
変量の測定値の最大値と最小値の幅.変動の大きさ(分布のバラツキ)の度合を表す.あるいは,非計量的測定値の要因効果の大きさを表現するときに用いられる.はずれ値の効果を受ける.計算結果のレンジはあまり問題ないが,ロウデータの場合には,最大値,最小値のほか,四分位範囲(上25%,下25%の範囲)などを並記する方がよい.
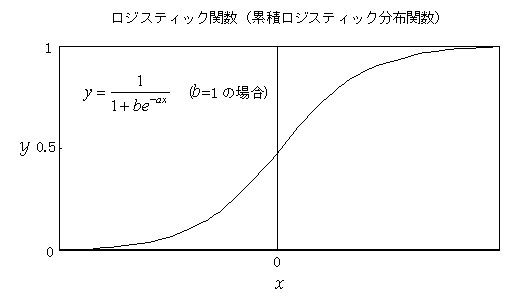
ロジスティック曲線(logistic curve)
y=1/{1+b exp(-ax)} 比率を応用しやすい数値に変換するときによく用いられる.100%と0%がそれぞれ+∝,-∝に対応する.比率をそのまま間隔尺度値として分析するよりも現象を妥当な形で取り扱うことができる.現実には100%や0%になることもあるので,最大最小を調整して適用することがある.ロジスティック関数は,比率の該当者と非該当者の両方に比例して変化する関数として導くことができるので,感染者の割合と非感染者の割合に依存して変化する伝染病のモデルとして使われることがあるほか,同じような現象である流行のモデルとしても使われることがある.クチコミや引用などの二次効果を考慮した場合には,情報の伝播のモデルや成長関数としても利用されることがある.対数オッズと線形的な関係にあるが,対数オッズをロジスティック関数の変化率の考え方から見ると,成功と失敗の両方に依存しており,成功率,失敗率が極めて高いときには,反対側の効果を無視するような対数関数的なウェイトが掛かることを示しているので,心理的な状況を良く記述している.ロジスティック関数(比率)が,該当,非該当の両方に比例することから導かれるが,比率が該当者の全体に対する割合であるので,比率の効果を,心理尺度値としての対数尺度上での差として捉えるならば,ロジット変換は,心理尺度上での当たりとはずれの差として理解でき,ロジスティック関数は,心理尺度上での差の問題を,測定値としての比率と心理尺度値(潜在変数)との関係を表した関数であると言える.対数関数は,指数関数とも密接に関連し,演算上かなり便利な関数であり,人間の行動をよく表現できるが,必ずしも,最適とは言えず,現象を記述するにはベキ関数の方が当てはまりがよい.ベキ関数などの関数に従ったオッズの分析や潜在変数の分析も行われている.(2003.3.13)
ロジスティック回帰分析
集計結果の比率データの要因分析(カテコリーの重回帰分析)のときに用いられる.比率は,0と1の間に分布するので,通常の回帰分析では推定に偏りが生じることがある.集計データ(ロウデータは該当非該当の2値)の回帰分析には,ロジスティック回帰分析のほか,ポアソン回帰分析(対数線形モデル),対数正規モデル,などが用いられることが多い.そのほか,ロジット変換(経験ロジット変換),プロビット変換,逆正弦変換などを適用して,通常の回帰分析を適用することもある.変換+最小2乗法(通常の回帰分析)では,データの範囲が大きくなると,ロジスティック回帰分析などの推定値との違いが大きくなるが,ほとんど一致する.そのほか,判別分析も同じデータの形式をしている.ロジスティック回帰分析は,該当と非該当の両方に結果が依存するような現象(2項分布など)に適している.目的変数は,該当数と非該当数の対数尺度上での差と大きく関係する.ポアソン回帰分析は,出現度数の小さい場合に適している.現象的には,非該当者の数が大きくて,全体数と非該当数を区別する必要がない場合に適している.目的変数は,該当者数の対数と全体数の対数との差と関係する.対数正規モデルは,全体数や,非該当数とは関係なく,現象が対数尺度上で正規分布すると仮定できる場合に適用する.対数正規モデルの場合には,目的変数を対数変換して,通常の回帰分析を適用するが,ロシスティック回帰分析は,目的変数が2項分布することを仮定して最尤法によって推定する.ポアソン回帰分析は,ポアソン分布を改定して,最尤法によって推定する.判別分析は,通常の回帰分析と解き方が同じであるが,もともと目的変数が固定している場合(2値の独立変数と同じ)と考えられる.
ロジット変換
y=log{p/(1-p)}による変換.pが比率のとき(0≦p<1),ロジット変換をすると,様々な現象を比較的矛盾なく取り扱うことができる.ロジット変換はロジスティック関数が適用できる現象を線形化できる変換である.対数オッズともいう.実際の分析では,0%と100%の数値にも対応できるように経験ロジットを用いることが多い.(サンプルが実際より1多いことにして,該当と非該当に0.5ずつ振り分けてロジットを計算する.経験ロジットの説明を参照)
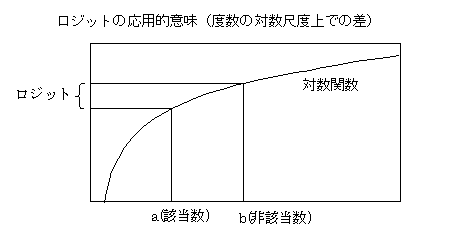
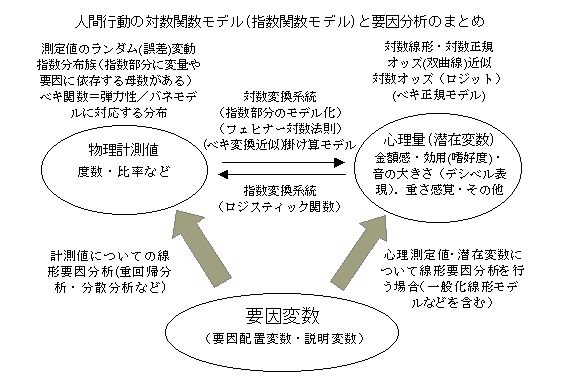
ロジットの根拠として,①経験的にその有効性が示されている.②二項分布を測定のランダム分布としたときの自然母数にあたる(完備な十分統計量を定義できるパラメータであり,正規分布の平均値のような役割をする),③潜在変数がロジスティック分布(応用上,正規分布に極めて近い)をするときの確率に当たる,というようなことが言われている.これらは,どれも否定できないが,次のような性質も持っている.全体をN,該当をa,非該当をb(a+b=N,p=a/N)で表すと,対数オッズは,logit=logp/(1-p)}=logp-log(1-p)=loga/N-logb/N=(loga-logN)-(logb-logN)=loga-logbと表現できる.これは,度数を対数変換して,対数尺度上での差がロジット変換値であることを示している.すなわち,通常のロジスティック関数は,合計が一定になる2つの数値の比を対数尺度上で差として取り扱っていることを表現しており,関数の形は比と潜在変数との関係を直接に表しているものと言える.対数尺度は,フェヒナーの対数法則をはじめ,心理的な尺度を良く近似するだけでなく,演算上極めて都合の良い性質を持っている.人間行動に関して取り扱われている測定値・誤差分布(ランダム変動)・要因分析・心理的尺度値(感覚量・嗜好度・潜在的変数)などを,全体的に理解しやすいようにまとめてみると,下のような図になる.(2003.3.13)
論理チェック(logical check)(データ入力のチェック)
質問票調査などの回答の矛盾をチェックすること.答えてはいけない部分に回答があったり,矛盾する回答があったりする場合,データの入力ミスとは別に回答者の勘違いや誤解による場合がある.「M-01 集計システム」の中に含まれている.集計システムによって省くこともできるが,データ自体が別の分析に利用されることがあるので,明らかなミスはデータ自体を修正しておく必要がある.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献