当社の業務で使用している用語を解説しています.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献
回帰分析(regression analysis)
目的となる変数(購入意向や快適感など,従属変数)と原因となる変数(独立変数)が測定されているデータから,独立変数と従属変数の関係を分析する方法.線形方程式を想定することが多い.すなわち,線形方程式の係数を求める.方程式が決まると,独立変数(原因となる変数)の数値が決まると,目的変数の量が計算できるので,原因となる変数から予測するために用いられる.
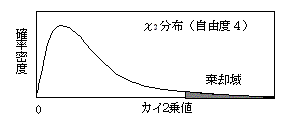
χ2検定(カイ2乗検定)
統計的仮説検定は、見出されたデータの傾向が偶然と言った方がよいのか否かを判定する方法であるが、その生起確率を計算するときに、χ2分布(カイ2乗分布)を用いた検定法.χ2分布(カイ2乗分布)が用いられる場合は多いが、代表的なものにクロス表の関連性(列要因と行要因の関連性)の検定,比率の差の検定、分布の適合性の検定などがある.

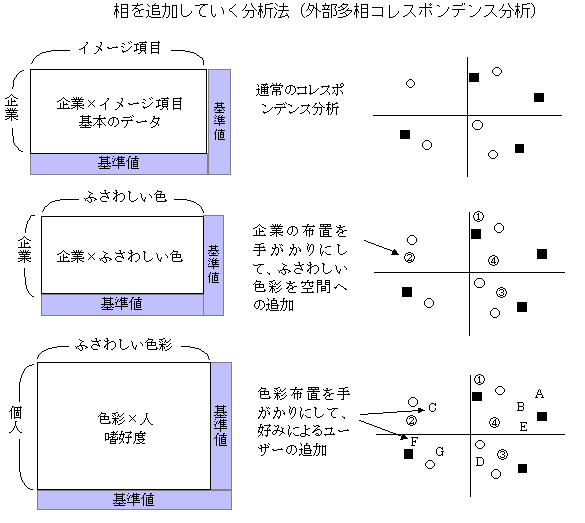
外部多相コレスポンデンス分析(external unfolding method)相の追加
既にできているマップに,要素を追加する方法をここでは外部分析(要素の追加法)と呼んでいるが、別の相(嗜好や第3の相)の要素を追加する方法が、外部3相コレスポンデンス分析になる。
基本的には、要素の追加法と同じ計算法になるが、すでにマッピングされている相と追加する相とのクロス表がデータになり、追加する相はそのデータの重心が原点になるように標準化される。すなわち、すでにできている標準化された相に、新たな標準化された要素を重ね合わせる分析法である。標準化された新たな相は、原理的には、次々と重ね合わせることが可能である。鎖状に連鎖させるので、実際には、互いに矛盾する相が現れたり、解釈できないような関連性が生じることがあるので、多くの相を表現することは難しい。(「コレスポンデンス分析の利用法」(2005)参照。)
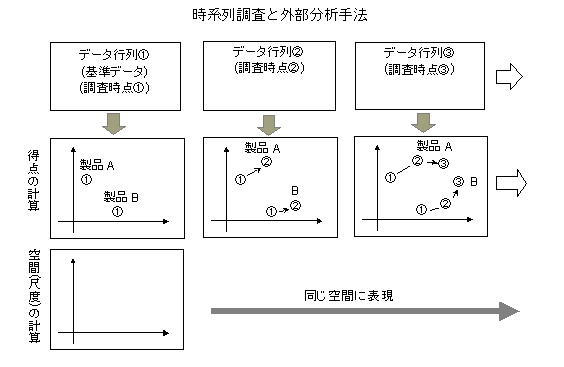
外部分析(external analysis)と内部分析(internal analysis)
外部分析とは,因子分析で言えば,既に分析された因子を用いて,新しいデータの得点のみを計算し,比較する方法である.一般に,因子分析や重回帰分析などの数量的な記述モデルでは,尺度(ものさし,因子)の構成の部分とその尺度によるサンプルや評価対象の得点計算(測定)の部分という2つの要素がある.因子分析の場合では,評価対象や属性(性別,年齢)の違いを見たいために妥当な因子尺度を決めたいというように,得点の計算が目的になること多い.外部分析手法とは,この尺度構成の部分と得点計算の部分を分離して,尺度(因子・次元・空間)に関しては,最初に作られたものを用いて,尺度値のみを計算する,という方法の総称として用いている.それぞれの分析方法が開発されたときに,既に外部分析手法が含まれているので,新しい分析法というわけではないが,応用上は,重要な概念である.よく使われる方法としては,因子分析の得点計算,数量化3類のサンプルスコア計算,クラスター分析の所属クラスターの判定,コレスポンデンス分析の行要素・列要素の追加比較,重回帰分析の得点予測,判別分析の判別,外部展開法(2次の項を含んだ重回帰予測)およびそれらの組み合わせである.そのほか,パス分析の得点予測,正準相関分析,分散分析,ノンメトリック回帰分析,その他の回帰分析などの応用例がある.応用上の問題点では,比較するために異なった測定において,条件が統制できるか否かということと,測定値の比較ができるように,尺度の位置を表わすパラメータ(ゼロ点)と単位を表わすパラメータを如何に調整するかということの2点が重要である.内部分析は,尺度を決めたデータの得点を意味することになる.応用場面では,外部分析の要請はかなり高い.「A-37 外部分析」参照.(2003.3.14)
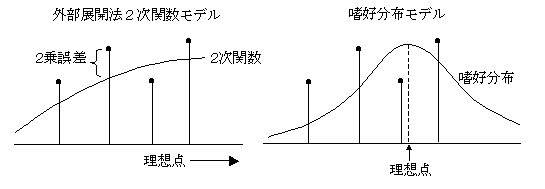
外部展開法(external unfolding method)
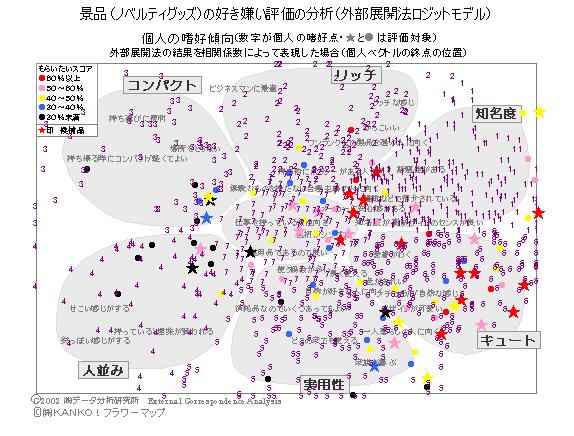
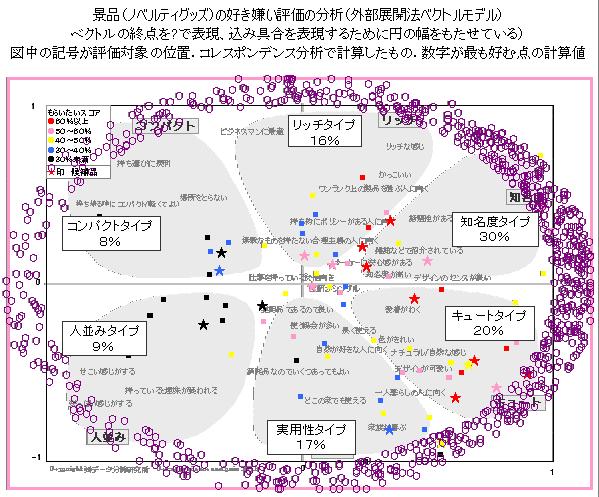
すでにできている空間布置に,嗜好の度合いを重ねる方法.一つの嗜好傾向を表現する場合は,地図上に天気図の等圧線を書き込むのに似ている.これは,空間布置に一つの新しい次元を付け加えることを意味する.外部展開法では,お椀をかぶせたような山形の嗜好傾向や平面全体に傾斜をする嗜好傾向を表現するような記述モデルを用いているので,最嗜好点(理想点)によって嗜好傾向を代表させたり,嗜好の傾斜を最嗜好方向を示す矢印によって表現したりする.試行の方向を求めるモデルは,通常の回帰分析と同じなので選好回帰と呼ばれることがある.また,2次関数のモデルは,古くから実験結果の応答曲面分析として知られている方法と同じである.一般的に,データの行要素と列要素を,同時に同一空間上に表現する方法は,展開法と呼ばれているが(コレスポンデンス分析もこの意味では展開法モデルの一つ),すでに空間が決まっている場合に,別のデータ(外部情報)を同一空間に位置づけるので,外部展開法と言われる(Carroll
& Chang,1972).
外部展開法は,嗜好度について,2乗誤差を最小にするように2次の項を含む(放物線的)回帰を求めて,その最大値を理想点(ideal point)とするが,曲線の当てはめは,データに敏感に反応するために理想点が想定される空間の外側に落ちることが多い.しかし,分析の目的においては,事前の空間の範囲をイメージして仮説が立てられるので,利用しにくい結果が出力される.当社のモデルでは,測定された嗜好度を確率密度値と考えて,空間に嗜好度分布を想定して,理想点を求めている.確率分布であるから,空間をはみ出すと適合度が下がる(尤度適合度)ので,理想点は,空間内にほぼ位置づけられる(分布の山の頂点).分布は,正規分布(プロビットモデル),ロジスティック分布(ロジットモデル),ガンベル分布(最大値モデル)などがあるが,どれでもほとんど同じ結果になる.最尤推定を行うと多次元のパラメータが同時に求まるが,累積ロジットを求めて次元ごとに最小2乗法で推定することもできる.(y=0のときのxの値が求める理想点の座標値).(2003.6.2)
価格とユーティリティ
価格は,多くのものや問題と係わっていることから,様々な評価の尺度として用いられている.物に限らず,労力や抽象的な価値についても価格で表現することが行われる.住宅の駅からの距離も価格に換算することができる.価格は,測定が価格であり,最終的な操作が価格の場合問題が少なく,合理的であると思われる.しかし,2つの価格の合計された価格が,2つの価格を別々に扱った場合と異なることがある.1000万円の一割引と1万円の1割引が同じように感じたりする.価格も物理的な要素が強いので,心理的な価値とは異なった刺激になることが考えられる.したがって,価格は尺度としてよりは,価値尺度の表現や換算用の値として取り扱うことが必要になる.人間にとっての価値は,抽象的で場合によっては価格尺度より不安定になる可能性があるが,基本的に価値尺度は物理的には定義できないような性質があるので,意識レベルの評価から構成せざるを得ない.できるならば,測定操作を厳密にした意識レベルの評価と価格の評価の両方の評価を行うことが有効性を大きくすると思われる.(2003.4).
学習曲線(成長曲線)
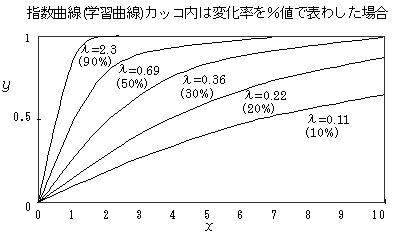
上限を持つ飽和モデルで指数曲線.比率のように上限を1にすれば、y=1-exp(-λx)のように表現できる。λは定数で飽和する速さと関係する。この関数は、比率の100%近くの1%と50%近くの1%では、実際の人間行動ではかなり意味が違うことなどを表現している.全体のうち、一定時間に残りの量の一定割合が変化するという考え方から導くことができる.学習課題の達成について、一定期間に残りの何割かが達成されるというように考える場合にあてはまる.学習曲線は、下の図のような形になる.広告効果の場合、広告投下量が一定であるとき、すでに知っている人を含めて一定の割合で情報が到達すると考えると、認知者が多ければ新しい人に当たる人数は小さくなることを意味するので、学習曲線がよく当てはまる。学習曲線が非該当者の割合のみに依存するのに対して、ロジスティック関数が該当者と非該当者の両方に依存する現象を記述している点が異なっている.学習曲線は,指数分布の累積分布関数にあたる.
確率関数(離散分布)・確率密度関数(連続分布)・累積分布関数
コインを10回投げる試行を数多く繰り返したとき,表が0回の場合,1回の場合,・・・,10回の場合に分布する.このとき,表の出る回数が確率変数であり,各変数に対応する割合が確率に当たる(二項分布).分布を関数で表現するとき,確率関数と言われる.正規分布のように確率変数が連続量である分布を,分布の形を表わす関数は,確率密度関数という.確率関数(離散分布)や確率密度関数(連続分布)を累積した場合の関数を累積分布関数とか分布関数という.累積分布関数は,応用的には,状態の移行を表現した場合(学習,購入経験,認知,伝染病感染など)その速さ(勾配)と飽和状態が同時に表現できるので,現象を理解しやすい場合が多い.
離散分布の場合には,確率は,全体の試行数に対する出現の割合になり,現実的な事象によく対応する.連続量の場合には,現実的には,離散量で与えられる確率変数を無限に細分化した場合に当たり,理論的に定義される.演算上は,連続分布の場合には,その確率が分布関数の積分値(面積)になる.連続分布が定義されたことにより,確率の問題が飛躍的に一般性を持ち,応用的にも広範囲に利用できるようになった.連続量の場合には,関数で表現される数値はf(x)は,離散的ではない確率なので,確率密度と言われる.現実的な確率事象は,数学的な一般的確率の近似として表現されることになる.(2003.4)
仮説検定→統計的仮説検定.
片側検定(one tailed test)
統計的仮説検定を行うとき,たとえば,平均の大小を比較するときなど,前もって,片方が大きいことが分かっていて,差があるかないかを検定する場合などは片側検定になる.確率分布の片方のみに棄却域を仮定する場合になる。どちらが大きいか前もって決められないときは、確率分布の両側に棄却域を仮定するので両側検定という.
カテゴリー(category)
質問項目について,項目をアイテムといい,回答選択肢(該当する項目の内容)をカテゴリーということがある.質問項目の場合には選択肢であったり,年齢などは該当する項目とか項目を用いなければ水準などと言えるが,データの構造上は,回答選択肢,年齢水準などのほか,調査後に作成する無回答や新しい分類項目(アフターコード)などを含めて,統一した用語としてカテゴリーという用語が用いられる.カテゴリーは,基本的に大小関係のない名義なので,カテゴリーから構成されている変数はカテゴリー変数と呼ばれている.心理測定学では名義尺度(nominal scale)の変数と言われる.
カテゴリーウェイトの計算
数量化1類、2類、3類などや分散分析の重回帰計算など、カテゴリー変数の場合、回帰係数を計算したあと、各項目のカテゴリーに対してのウェイトを計算し直す必要がある。回帰係数は、要因変数1単位に対するウェイト(効果量)なので、分析に用いたデータ数を考慮したウェイトではない。分析に用いたデータは、標本分布するので、その分布を考慮して平均0分散1になるように標準化した得点になるようにウェイトを変換するのが普通である。このことによって、該当するカテゴリーのウェイトを加算すると、そのサンプルの標準得点が得られる。計算は、手順図のようになる。

カテゴリーバイアス
嗜好度や購入意向などの心理量を測定するとき,必ず数量の表現法の制約を受ける.やや好き,大変好きというようなカテゴリーによって数値を表現するとき,そのまま整数値を与えて数量的な分析をすることがある.通常の場合,大量のデータを処理するには便利であり,非常に有効な方法である.カテゴリーバイアスとは,カテゴリーを用いたときに見られる系統的な歪みのことを言う.一般的には,使用するカテゴリーの幅が中央付近では広く,両端では狭くなる傾向がある.カテゴリー判断は,厳密には間隔尺度ではないが,順序尺度以上の情報が得られるので,カテゴリーバイアスが,分析結果に系統的な歪みが明確ではない場合には,有効に利用できる.
カテゴリカー重回帰分析
独立変数がカテゴリカルな変数(大小関係のない測定項目,性別や職業など)のときの重回帰分析.数量化1類と同じ.基本的には,01型のデータと考えて,最小2乗法によって解く.カテゴリーを変数に変換する方法としては,01型のダミーコーディングの他,効果コーディング,直交コーディングなどがある.「A-55
重回帰分析の利用法」、「M-11 重回帰分析法」(プログラム).
間隔尺度(interval scale)→測定値のレベル.
環境評価法
心理的な快適さや価値を測定する場合には,心理測定法が利用される.評定法,一対比較評定法や一対比較恒常和法など.要因を評価する場合にはコンジョイント分析のようにトレードオフ順位法やフルプロファイル評価法を用いると分散分析モデルや重回帰モデルによってシミュレーションが可能である.環境は,政策コストと結びついていることが多いので,CVMやヘドニック法,トラベルコスト法などのように費用金額を尺度として使用することもある.どの方法を用いるにしても,サンプリングの妥当性がが,結果を利用できるか否かについて,最も重要な問題になる.
官能検査(sensory test)
官能評価(sensory evaluation)ということもある.人間の感覚を用いた検査や人間の嗜好傾向によって製品などを検査すること.心理学分野の感覚研究や判断プロセス,尺度法の研究が多く利用されているが,応用的な必要性が前提にあることから,測定法,統計分析,検定法が中心であり,様々な技術が独自に開発されてきた.また,具体的な問題解決の必要上,心理学に限らず,統計学や実験計画,経済学や意志決定,消費者行動,工学,医学,情報処理などのほか,関係する領域(食品,様々な製品,環境,建築,都市設計など)などの広い研究分野の知見を利用することになる.
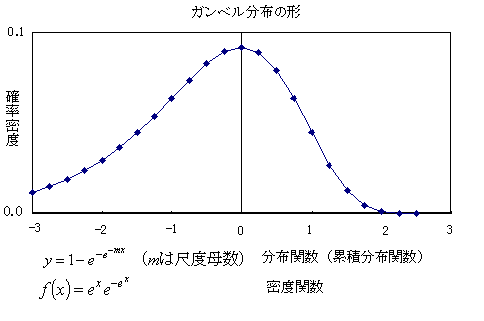
ガンベル分布Gumbel distributuon(2重指数分布)
式では,指数部分に更に指数関数が入っているので,2重の指数の形になっている.正規分布などの指数型分布をする事象に関して,幾つかのサンプルの最大値の分布のように,指数型分布を想定できる現象は,2重の指数分布の形なると理解することができる.理論的には,最大値の事象からのサンプリングすれば,3重の指数分布を構成することができるが,応用的な意味がなくなってくる.
嗜好度が正規分布的にランダム変動する複数の製品から,最も好む製品を選択する場合には嗜好度の最大値のものを選択すると考えられるので,ガンベル分布をすると考えられる.このような考え方から導かれる選択行動のモデルとして多項ロジットモデルがあり,ガンベル分布がよく使われるようになった.多項ロジットモデルは多変数のロジットモデル(ロジスティック回帰分析)などの統計的解析法との関連で議論されることが多いが,商品などの選択行動モデルの立場からは,リュースの選択行動モデルに対してランダム変動を想定しているのでランダム効用モデルと言われる.ガンベル分布のような極値分布(最大値分布)を一般化したものに一般化極値モデルGEVモデル)がある.
危険率
統計的仮説検定法において,帰無仮説を棄却するとき(証明したい事象が起こったと結論するとき),偶然に事象が出現する可能性.誤りの可能性を示す。第1種の誤り(type Ⅰ error)の率を表す.有意水準と同じ.確率的に結論するときには,必ず,危険率を伴う.
基準化(normalization)
標準化ともいう.データベクトルを平均が0,分散が1になるように変換すること.この操作によって,原点と単位の異なる測定値が基準化の制約のもとで比較できるようになる.たとえば,身長と体重は単位が異なるので,数値自体を比較することには意味がない.体重50kgと身長50cmは等しいとは言えない.しかし,一般に,「体重の割には身長が高い」など,身長と体重を比較して評価することがある.また,満点や平均値,難しさの違うテストであっても,「英語はできるが国語はできない」というような比較をする.このような比較は,数値や得点そのものを比較しているのではなく,平均からの偏差や順位など,それぞれの数値を相対的な尺度値に変換して比較していると考えられる.統計学的な基準化(標準化)は,これらの人間の相対的な比較機能を表現したモデルとも考えることができる.
QDA,キューディーエー(quantitative descriptive analysis)
多数の評定尺度によって刺激の特性を評価する官能検査の方法.多くの官能評価法は,測定する側面が嗜好度,差異(違い),など単一次元のことが多く,評定,一対比較,順位,識別など問題によって測定手続きを変えて利用する.QDAは,多数の評価尺度を用いて刺激の側面を測定することが特徴である.測定法自体は評定尺度法である.同じ様な評定尺度による多側面の測定法としてSD法と呼ばれる方法がある.分析法も,各評価次元を一つずつ見ることの他に因子分析などによる多次元の分析をすることが多い.
共分散行列・相関行列・積和行列・基準化積和行列
一般に,因子分析などには相関行列が用いられる.相関行列は,複数の測定尺度間の原点と単位(分散)が共通に用いられない場合に適用される.身長と体重や環境要因などからそれらの関連性を見るとき,単位の違いに意味がないし,原点についても,特別な場合を除いて意味がない.したがって,原点をそれぞれの平均値に決め,単位を標準偏差にとって,積和(内積)を計算することによって,変数間の関連度を表現する.内積は,変数の分散(個々のデータの個別のばらつき度)を見たとき,片方の変数の大小(体重の大小)ともう一方の変数の大小(身長の大小)とが同時に変化する割合を表現するので,関連度としてはふさわしい指標と言える.平均と標準偏差によって標準化されたデータの分散は1になる.
平均値の大小に意味がなく,分散の大きさに意味があるときには,分散共分散行列が有効である.平均値に意味がないということは,測定尺度が相対的な場合である.たとえば,基準が与えられて,それと比較した結果であり,基準が時と場合によって変化するとき,あるいは,測定の原点を「ない」ことと理解すること問題がある場合である.分散の大きさに意味があるとは,分散が評価対象の差異の識別の指標に使える場合である.味の評価の場合,分散が大きければ,違いを明確に区別し,分散が小さければ違いが区別されていない,というような場合に当たる.このようなデータについて,分散共分散行列を用いて,次元縮小の因子分析(主成分分析と単純構造変換)を用いると,識別力のない尺度は,因子に寄与せず,結果的に因子構成上無視されることになるので,データにより忠実な結果を出力する.小さな分散が,測定尺度によって起こる場合(学力テストなどによく起こる)では,尺度に意味がありそうであっても相関係数の方が現象を正確に表現している可能性が高い.共分散行列は感覚関係の現象に用いられる.
測定の原点に意味があり(ゼロということ),単位にも意味があるとして,分析したい場合には,積和行列を用いる.出現率があまり高くない度数データなどのとき,積和行列の因子分析をすると,変数の関連性と総合的に反応率の高さに意味を持つ因子が抽出される.項目の分類というよりは,反応を持つ対称を,単一項目より信頼性の高い幾つかの項目の合計点によって検出するという目的に適している.積和行列の分析例はあまり多くないが,異常現象の尺度化(異常行動の相関関係),極端な特徴の片側尺度化(商品や人間のイメージや態度のプラスに極端なものの識別など)の適用例がある.ポアソン分布をするような現象の場合,目的によっては,対数変換しないデータの積和行列を因子分析するとデータをよく要約できることがある.
理論的には,2乗和で基準化した場合の積和行列もある.これは,原点の意味は生かすが,尺度自体の単位は基準化するという方法であり,変動係数の目的に似ている(変動係数は平均値を用いる).応用例はあまり多くないが,積和の因子分析が,極端な結果になるので,技術的な調整として用いると,相関行列の因子分析に原点の制約を与えたようになり,積和行列の分析より使いやすいし,相関行列の場合と違って,マイナスの因子負荷が出にくいので使いやすい.(2003.4)
共分散分析
分散分析を行うとき,一見,差がないように見えたり,差があるように見えたりするとき,他の変数を考慮すると結果が変わることがある.オフィスの快適性を評価したとき,性差が見られることが多いが,女性の就業者が比較的若いことから,年齢差を考慮すると性差がなくなったりする.このような要因を交絡要因と言うことがある.もともと共分散分析というときには,年齢による回帰傾向を調整したときの性差の分析というように回帰直線の切片の差の検定(回帰分析による交絡要因の除去後の分散分析)ということを指している.交絡要因を逆にすると,相関関係がないような結果に見えるが,例えば2つの回帰傾向が重なっているために回帰傾向が見えなくなることがある.たとえば,会社に対する不満度と収入の関係を見たとき,比較的高齢者の不満が高いと収入が高いと不満が大きくなるという関係が出てくる.年齢別に分析すると逆の関係になる.この場合,年齢を分ける変数を01型で加えると収入が低いと不満が高いという関係が出てくる.層別要因も連続変量も同等に考えられるので,一般的には,付け加えるべき要因を考慮したときの要因分析法と言え,回帰分析の偏回帰の問題になる.
共分散構造分析
複数の変数間の関係を表現したモデルが複数想定される場合には,パス分析などがある.線形関係を表現したモデルには,重回帰分析の場合のように従属変数と予測変数の因果関係だけでなく,単純な変数の平均による合成変数の構成や加重平均などの一種の因子分析モデルもある.主成分は加重平均の一つの例である.これらの変数間の関係は複数の線形方程式によって表現できる.一組の対応する変数のデータから,そのデータ数が十分であれば,複数の関係式のパラメータ(係数,変数のウェイト)は,誤差分散の正規性や複数の誤差の独立性などを仮定し,適当な制約を加えると,一度に解くことができる.関係式が多くなると,未知数とデータ数の関係(識別可能性)や制約条件を指定することが難しくなる.
共分散構造分析の場合の回帰係数は、通常の重回帰係数と同様に、説明変数が独立変数(本来的に相関関係を持たない変数)ではない場合、解釈できない数値を出力することも前提にしているので、調査などの場合、かなり適用を制限された方法になる。一般に、因果関係の部分は、妥当な形で解釈できないことが多く、単相関係数の方が有効なことが多い(「データ分析入門2」など参照)。
極限法(method of limits)・極小変化法(method of minimal changes)
音などについて,人間にとって聞こえる大きさ(高さ)を測定するときなどに用いられることがある.聞こえる音の大きさは絶対閾(ぜったいいき)と言われる.実際の測定では,絶対閾は,聞こえるような気がする程度に感じるものであるから,被験者は確信が持てないのが普通であるので,統計的に定義せざるを得ない.極限法で測定するときには,聞こえないような小さい音から順に大きくしていって,聞こえたと感じた時点で止める.逆に明らかに聞こえる音からはじめて,徐々に小さくしていき聞こえなくなったと感じた時点で止める.一般に,上昇系列と下降系列では結果が一致することはなく,何回か繰り返して,平均的な値を求めて絶対閾であると定義する.極限法は,弁別閾の測定にも利用される.絶対閾の測定には恒常法なども用いられる.人間の知覚機能を研究するために用いられることが多いが,応用では,味の変化に気づく量(甘さ,塩辛さ,香料など),重量の変化など,商品開発(官能検査)に用いられることがある.心理物理的測定法として,結果が歪まないような手続きが確立している.(2003.4)
曲線回帰
曲線的な傾向線について,偏差2乗和を最小にする方法(最小2乗法)で推定する方法.曲線の関数形は分かっている場合には,比較的簡単に曲線のパラメータを決めることができるが,データから関数形を決める必要がある場合には,独立変数の2乗,3乗,・・・の項の有意性を検討しながら関数形を決めたり,測定値の変換(対数変換,逆数など)をいわば試行錯誤的に行って当てはまりの良さを調べたりする.測定値が多数ある場合には,独立変数の大きさによってグループかして平均をプロットすると,傾向線をデータに合わせて求めることができる(適合度は相関比).階差(隣の数値との差)と独立変数との関係を2階(階差の階差),3階と調べるなどして,関数形を推定する.階差は,微分係数(速度に対応する).一般には,理論的に関数形は,おおよそ分かっていることが多いので,求めるパラメータ(未知数)を含んだまま偏差2乗和を定義して,最小値問題として解くことができる.ロジスティック関数など誤差分散が明らかに正規分布しない場合には,誤差分布(測定のランダム成分)が定義できれば最尤法などを用いることができる.
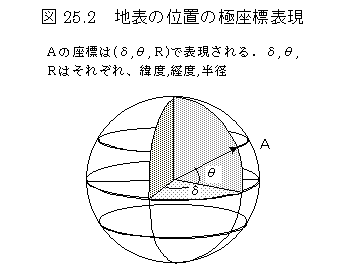
極座標
座標の位置を表すのに,座標軸との角度と原点からの距離を用いる方法.ベクトル表現に近い.地球上のように原点からほぼ一定の距離にある地表では,角度が距離よりも便利なことが多い.人間は空間把握(地図など)は基本的に方向と距離を用いるので,人間のモデルとしてよく適合する.
クラスカルのノンメトリックMDS(Kruskul's non-metric MDS)→ノンメトリックMDS.
クラスターの判定法(クラスターの外部分析)
すでに決まっているクラスターについて,新しい対象がどれに属するかを判定する方法.「A-59クラスター分析」 解説書.「M-17クラスター分析」プログラム.
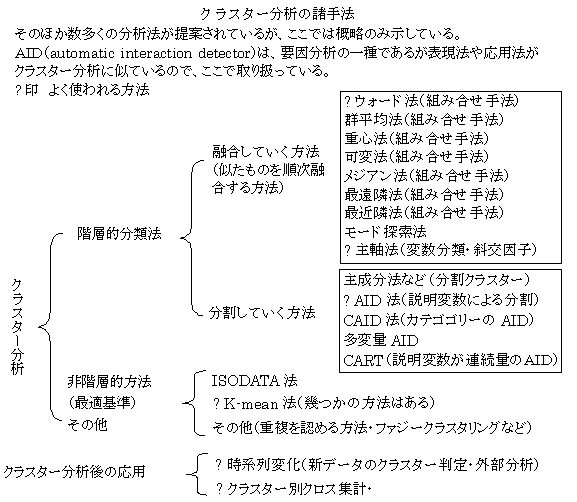
クラスター分析(cluster analysis)
人 人や物など多数の対象について,似ているものをまとめて,典型的なタイプを探す方法.まとめられた群をクラスターという。数多くの方法がある。明確な群のまとまりがあるならば,どのような方法を用いても、群が見つかると思われる.似ている対象を順次融合しながら,似ている対象をまとめる階層的な方法は、樹状図(トゥリー、デンドログラム)を描くことができ、視覚的に理解しやすいので、多く利用されている。昔は、計算機容量に制限されたが、現在は、1000対象など比較的簡単に計算できるので、利用しやすくなっている。
群数を事前に決めて、群分けの最適基準を実現する非階層的な方法は、信頼できる群が抽出されるが、事前に群数を決めたり、各群の初期値(シーズ点)を決める必要がある。計算しながら群数を変えることや、重心が修正されて、最適な結果になる。
応用的には、厳密な最適さよりも、解釈しやすさなどによって、幾つかの結果から選択するという使い勝手のよいことが好まれるので、階層的な方法が多く使われている。
質問項目をそのまま使うと,互いに相関を持つ項目が重視されてしまうので,独立したクラスターが得られなかったり,項目の一致度の偶然性が高くなったりして,解釈しにくいクラスターが形成される可能性がある.実際には、プロットされた因子得点をグルーピングしたり、プロットされた数量化3類のサンプルスコアをまとめること、MDSやコレスポンデンス分析の空間(マップ)などの得点をまとめることなどに利用される。
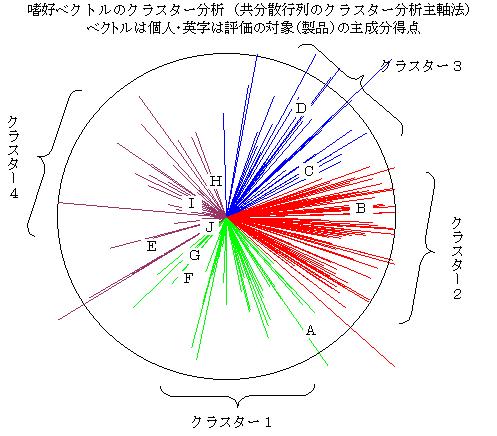
クラスター分析主軸法
相関行列などのクラスター分析の場合、距離を分類の基準にするよりも、相関係数(ベクトルの内積)を用いた方が自然である。相関係数を融合基準にした場合、融合後の値は、平均値(セントロイド)よりも主成分(主軸)を用いると球面上の距離を良く表現できる。新たな相関(角度、方向余弦、内積)は、主成分間の角度によって表現される。このように、融合された群の主成分(主軸)を計算しながらクラスターを構成する。分析結果は、斜交の因子分析とも言える。図は、嗜好度の評価結果に共分散行列の主成分分析を適用して、対象の布置を求め、2次元に主成分負荷量を基準化して(長さを1にして)、主軸クラスター分析を適用した場合である。
繰り返しが不揃いの分散分析法
分散分析(実験計画)では,要因が直交していないと検出力が極端に落ちるので,実験をする場合には,繰り返し数を一定にするなどの要因配置を立てる.欠測値がある場合はそのまま分析すると,要因が直交しなくなる.やむを得ず欠測値が出た場合には推定した方がよい.最小2乗推定が全体の結果に馴染む推定値になる.調査など,繰り返しを揃えることを目的にしないこともある.欠測値を推定しないときには要因が直交しない場合の分散分析になり,その場合,分散が要因に分割されず,どの要因に入れたらよいのか分からない部分がでる.一般的には,もっとも消極的に考えて,判定できる分散のみを検定することになる.
グループ主軸法(group axis method)
斜交因子を求める方法.前もって項目のグループを決めておいて,グループごとに主軸(主成分)を求める方法.軸(因子)の内容を前もって決めるので,因子の確認的な利用法になる.因子を利用する場合,因子が互いに直交するようなイメージを持つことが多いので,斜交因子の分析後,さらに直交因子を求めることもある.「M-10因子分析法」 因子分析のプルグラムに含まれている.
クロス集計
単純集計(Grand total,GT)に対して,性別,年齢別,特定の質問項目の回答などによって分けて集計すること.コンピュータを使わない場合には,クロス項目の回答によって分けてから,別々に集計分類作業をするので手間がかかったが,コンピュータが利用できるようになって,単純集計とクロス集計がほとんど同じ程度の作業量でできるようになった.クロス集計表を見るときには,全体の度数の大小の効果を除くために,パーセントの形にし,さらに絶対的なパーセントの大きさではなく,全体のパーセント値(あるいは比較対照のパーセント値)との大小比較をして結論を出す.このようなパーセント値に直した後,さらに,そのパーセント値の比較をするという方法は,周辺度数の絶対的な大きさを調整するカイ2乗統計量の大小をみるのと同じであり,このような見方から,行要素と列要素の関連を図的に表現する方法がコレスポンデンス分析の考え方と言える.→コレスポンデンス分析.
クロンバック(Cronbach)のα
測定された項目得点を合計した得点の一貫性の指標。合計した得点と他の変数との関係を分析するときの信頼性を表す。たとえば、項目の合計得点について性差を見るとき、α係数が小さいと、得点のバラツキの中に個人差や性差のバラツキのほか、得点を合計したことによるバラツキ(項目の意味が異なることによるバラツキ)が多く含まれるので、性差が検出ににくくなる。したがって、α係数の大きな合計点を用いなければならない。α係数は、項目間の相関がマイナスのとき、負の値になることもあるが、その場合には項目得点を逆転させれば正の値になるので、一般には、0から1の間の数値になる。決定係数と同様に分散の割合を表現しているので、0.8、0.9などの数値が望まれる。合計される個々の項目が、同じ測定内容を別々に測定したと考えると、α係数は信頼性係数の一つの推定値(下限値)を表している。信頼性係数やα係数については、池田央「調査と測定」新曜社、「心理学研究法テストⅡ」東大出版など参照。
景観の評価
当社では,複数項目の評定法(SD型評定法)によって評価する.多くの写真を用いて,目的に評価対象をその中に含めておき,相対的な位置を明らかにする.
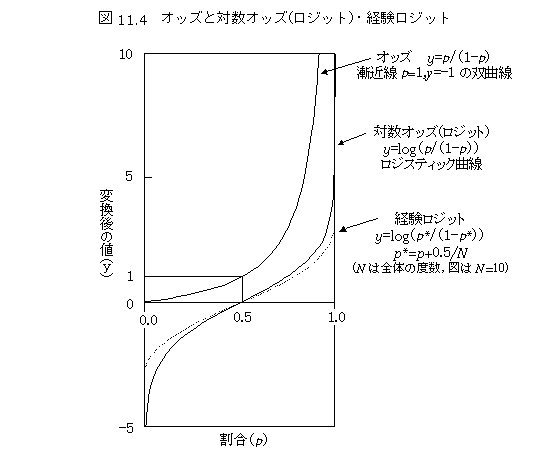
経験ロジット(empirical logit)
比率が0%になったり,100%になるときロジットは-∞と+∞になり,不都合になる.実際のデータでは,0%や100%は出現することがある.そこで,全体の度数に1を加え,0.5を該当と非該当に加えて,決して0%と100%にならないようにしておくことがよく行われる.サンプルが30の場合の100%の経験ロジットは,自然対数で約4.11になる.関数形としては,ロジスティック関数の漸近線がy=1よりも少し大きく,y=0より少し小さい所にくるので,100%と0%がy=1とy=0の直線と交差することになる.実際のデータを取り扱ってみると,0%と100%の問題だけでなく,比率がかなり大きい場合やかなり小さい場合には,ロジスティック関数の当てはまりが悪くなる感じがするので,常に経験ロジットの方を使いたくなる.100%の問題は,累積指数分布や累積ワイブル分布の場合にもよく起こる問題であるので,経験ロジットと同じ考え方で漸近線の位置を修正することがある.
K-MEAN法
非階層的クラスター分析の一つ。初期値を与え、各クラスターに属するメンバーを決める。クラスターの凝集度によって、初期値から群を増やしたり、減らしたりして、妥当なクラスターを決める。反復計算を行い、メンバーの所属が安定するまで続けるが、だいたい数回の反復で安定した解に到達することが多い。
系列効果(series effect)
人間の評価行動における系列効果は,官能評価の順序効果のような現象として観察される.人間の機能の側から見ると,回答の言葉の連続性の問題と刺激の効果に分けられる.刺激の効果は,同じ刺激であっても全体の中の位置の効果(文脈効果,系列位置効果)と直前刺激の残存効果に分けられる.どちらにしても,系列に考慮して,ランダム順提示,順序の逆提示によって,だいたい取り除くことができる.
欠測値の処理
欠測値は,本来,測定内容とは無関係な要因によって起こる場合であるが,実際のデータでは、読み飛ばしや誤解のほか,回答を躊躇したり拒否をしている場合、内容的に該当しない場合、質問の意味が不明の場合、などが多い.無回答があっても,分析をすることになるが,欠測値の処理には,次のような方法が採られる。欠測値に代入する数値またはカテゴリーを指定する(中性カテゴリーや中間値)方法.カテゴリーの場合,無回答カテゴリーを作ることもある.項目の平均値や最頻カテゴリーを代入する方法.無回答を使用しない方法(変数レベルの分析では無回答項目を除いたものを全体とし、サンプルベースの分析ではそのサンプルを除いたり、測定項目を除く).サンプルの平均値や最頻数を代入する方法.最小2乗推定をする方法(他の項目との相関関係から推定する方法で重回帰予測か判別予測をする).欠測値の部分のみ用いない解析法を使う場合(欠測値のみを用いない方法は、特定の推定値を代入する方法と等価な場合が多い).欠測値が多かったり、クラスター分析のようにサンプルの情報を直接用いる方法は、最小2乗推定が欠測値を用いない解析ほうよりも安定した結果のなることが多い。欠測値を用いない解析法は、他のデータの傾向のみから推定するので小さくまとまる特徴があるのに対して,最小2乗推定は、変数間の関連性を元にするので、意味をもってバラツク推定値が得られる.
検出力
統計的仮説検定において,実験や調査が持っている証明したいことを検出できる力.たとえば,2つの条件に差があることを証明したいとき,データ数が多い場合と少ない場合とを比較すると,測定された差が同じであっても,データ数が多い方が偶然ではないと言えることが多い(有意差あり).これは,データ数が多い方が検出力が高いことを意味している.検出力はデータ数だけでなく,実験の精密さ(分散の大きさ)や検定方法などにも関係する.
検定法→統計的仮説検定
ケンドールの順位の一致性検定
複数の人が順位を付けたときの一致性を確率的に検定する方法.確率は超幾何分布を利用するので,データ数が多い場合には,カイ2乗分布で近似できる.一致しているとは言えない場合には,順位数をそのまま使うか,変換したり,ノンメトリックな方法で順位の多次元解析をすると,順位付けが多次元なのか,誤差が大きいのかなどの判断ができる.
効果コーディングeffect coding
カテゴリー変数について数量的な分析をするときに,カテゴリーを変数として表現する必要がある。ダミーコーディング、効果コーディング、直交コーディングなどがよく使われる。図のように、最後のカテゴリーにすべて-1を与え、他のカテゴリーは、該当するカテゴリーの変数の1を与える。ダミーコーディングの最後のカテゴリーに-1を与えた場合になる。
要因分析の説明変数に使用する場合、3つのカテゴリーは2次元平面を形成する(ランクが2)。異なった3点が平面を形成するのと同じ。要因分析の場合、平面に対する目的変数の射影が問題となるので、どのような点をとって平面を形成しても構わない。したがって、3つのカテゴリーに与える数値は無数になる。ダミーコーディングは、最後のカテゴリーを基準にして(0として)、各カテゴリーの効果(回帰係数)が基準からの差異になるように決める方法であるが、効果コーディングは、コーディングされた変数の各点が、1、0、-1の3つで構成され、バランスをとった形になっているので、交互作用が変数コーディング変数の掛け算することによって、元の変数と直交するようになる。したがって、要因間の交互作用を重回帰分析によって表現するときに都合がよい(ダミーコーディングなどは、変数を掛け算したとき交互作用が直交しない)。高次の交互作用もコーディング変数の掛け算によって表現できる。詳しい内容は,「A-55重回帰分析の利用法」(2004刊)参照.

広告効果
一般に,製品の知名率(認知率)の大小を問題にする場合が多い.知名率をあげるには,GRPなどの広告接触の可能性を表した量(広告出稿量と単純な1次関係にある)と認知率との関係が問題になる.1方向的な情報の流れ(TVや新聞,雑誌の広告など)の場合には,指数曲線が当てはまると言われている.販売量と広告との関係を見るためには,広告の内容と消費者のニーズなどの把握が必要となる.広告効果測定を広い意味で捉えると,「広告による態度の変容」「広告の質や社会性の評価」なども含むことができる.
広告による態度変容
広告効果のうち,とくに,広告によって内容の理解や嗜好の度合いの変化が起こること.一般に広告効果と言ったとき,知名度の変化を指すことが多いが,内容の変化を測定したいことがある.内容理解の変化は,広告視聴の前と後でマインドシェアを測定やイメージ評価の変化を測定したり,インタビューによる自由な印象評価などを測定する.
広告評価
広告の特徴評価のうち,とくに,広告そのものの特徴を評価する場合に限って広告評価と言うことがある.おもに,デザイン的な要素の評価,映像的な評価,文章の正確さと誤解の可能性,わかりやすさ,演出効果と内容表現の逸脱,広告の社会性など,広告のインパクトの強さなどの広告効果測定とは別の側面の評価も含まれる.
交互最小2乗法(alternative least square method)
パラメーターが多くて通常の最小2乗法では推定できないような場合、適当な初期値を与えて、未知数の一部分を最小2乗法で推定し、推定された値を用いて、残りの未知数を最小2乗推定する。未知数を交互に変えながら収束するまで繰り返す。計算された数値より誤差を小さくすることを繰り返すので、一定の推定値に収束することが予想できるが、極小値である可能性がある。交互最小2乗法には、未知数を3分類したり、同一の推定パラメータを別のステップで重ねて推定したりするなど,かなり自由に未知数を決めることができるが、一定の数値を代入したときに、モデル式が最小2乗法が適用できる形になっていなければならない。最適化計算は,必ずしも最小2乗法である必要ななく,最急降下法やニュートン法などを用いても同じように解くことができる.
自由度が小さい場合には、基本的に、一つの測定値が多くの推定値にかかわるので、推定値が平均的に小さくまとまる傾向がでることは、最尤法や他の推定法に関わらず自由度の小さいデータの推定結果の特徴である。また,交互に分析するとき,推定パラメータのデータを記述する能力(誤差を小さくする機能)に偏りがあるとき,自由度が小さいので,記述能力の大きい(パラメータ数が多い場合など)方が,優位に推定されるという傾向が出る.本来,識別できないような分散(どちらの原因かわからない部分)を適当に振り分けている可能性があるので,必然的結果と言うよりは,1つの解釈,と言う意味になる場合がある.パラメータ数などは均等にした方が安全であるほか,できるだけ,交互最小2乗法は用いない推定法が望まれる.データ分析モデルでは、INDSCALの正準分解法が交互最小2乗法であるほか、ALSCALは名前の示されているように交互最小2乗法を用いている(当社では、特別の制約がない場合、コーホート分析を交互最小2乗法で解いている).(2003.3.18)
交互作用の多重比較
分散分析によって,交互作用が見出されたとき,特定の刺激の組み合わせのみの分散が大きい場合がある.主効果の多重比較も同じことが言えるが,分析結果を応用するときには,大きな枠組みとして細部を検討した方がよいか,細部を見ても生産的な方向性が見出せるか否か,というような見方がまず必要になり,現象としての交互作用は,どこかに一部分の突出した効果によるのか,全体的な交互作用機能があるのかということが次の問題になる.そのためには,結果を見誤らないような図(グラフ)表現によって全体を見渡すことが必要となり,数値的な結果は,その判断の妥当性を裏付けるような役割として利用する.その意味で,交互作用を理解するときには,データから主効果(平均効果)を取り除いた部分のみをグラフ化したり,要因が直交しない場合には,度数のウェイトを付けたときのグラフ表現が必要になる.「A-63分散分析における多重比較の応用的意味」参照.
恒常誤差(constant error)
測定する場合,系統的に入り込む誤差.測定値を特定の方向に歪める可能性がある.心理測定法は,恒常誤差を避けるために工夫されているといってもよい.味などの順序効果はその例.今まで,数多くの種類が報告されている.
恒常法(constant method)
心理物理的測定法の1つ.主観的等価値(比較対照として与えられた刺激と主観的に感じる刺激が異なっている場合の測定値,錯視量,時間誤差,系列効果などの広い意味の錯覚量の測定)や弁別閾(標準刺激と異なって感じられる量)の測定などに用いられる.複数の量の異なった刺激を用意して,標準刺激と多数回比較させ,回答の割合に正規分布などを適用して,測定値を求める.
恒常和法(constant sum method)
全体の得点を決めておいて,評価するいくつかの対象に得点を振り分けて,程度を表現する測定法.10個または11個のチップを好きな程度によって振り分けるチップゲームと呼ばれるマインドシェアを測定する方法がよく用いられている.対象の一対を比較する操作をすべての組み合わせについて行うことが多い.心理測定上は,比率の直接測定法として位置付けられる.開発当初は,比率の平均操作に苦心したが(ギルフォード,1954参照),対数変換して平均する方法(幾何平均)が比率平均の矛盾を解決した(田中,1961参照j).その後,①対数平均と最小2乗法,②正規分布を利用したプロビット変換と最小2乗法,③二項分布を想定した最尤推定法などにまとまられた(印東他,1977参照).現在では,対数変換はロジスティックモデル,二項分布の解析法はロジスティック回帰分析に帰着するとして,不完備型の分析にも比較的簡単に対応できることが理解されている.さらに,ランダム効用関数モデルの考え方から,多項ロジットモデル,多項プロビットモデル,入れ子型多項ロジットモデルのほか,より一般的な一般化極値分布モデルなどを利用して解くことが可能である(データ分析研究所,2003参照).「B-11 恒常和法によるマインドシェアの推定法」(解説書).「M-18 恒常和法とマインドシェア予測プログラムマニュアル,ロジットモデル」.「vbソフト」(Windows用,当社開発)など参照.
コーホート分析(cohort analysis)
コーホートは、メンバーが固定された群のことを意味するが、データ分析上は、生まれた年がほぼ同一の集団をコーホートと言い、その集団の、とくに時間の推移によって変化しない部分を取り出すことをコーホート分析と呼ぶことが多い。具体的には、時系列的なデータを規定する要因として、加齢による変化(年代効果)、調査測定時期の変化(時代効果)、生まれ年による差異(世代効果、コーホート効果)を区別することが分析の目的になっている。実際に分析をする場合には、要因が同時に変化してしまうので、通常の要因分析法では解けないので、加齢効果、時代変化、世代効果などに連続性の関数を仮定したりして解く。(当社では、内容によって既存のモデルを用いるほか、特別の制約がない場合には交互最小2乗法を用いる.比率のデータや集計度数のデータの場合,該当非該当の両方に依存するときのロジスティック回帰分析,出現率の少ないときのポアソン回帰分析や,ロジット変換等の変換と最小2乗法など時と場合によって使い分けている)
コクラン・アーミテッジの傾向検定(Cochran-Armitage trend test)
ノンパラメトリックな傾向検定.大小関係のある特性を持ついくつかの群があるとき(使用頻度の多少など),各群の中の該当者率(良いと答えた人など)に違いがあるかないかを検定する方法.医学などでは,オッズ比(危険度のオッズ表現)の傾向検定の方法として用いられることが多い.各群に数値を与え,全体の内積(相関)と群内の相関とを比較する形になる.各群に群の順位を与えたり,順位に群の度数の重みを付けた数値を用いたり(ウィルコクスンの順位和検定),外的に定義できる数値を与えたりすることができる.「M-53統計的仮説検定」にプログラムがある.
個人差を考慮した多次元解析法
距離行列が個人別にある場合(2相3元データ)や評価対象を複数項目で評価したデータが個人別にある場合(3相3元データ)では,MDSの刺激の布置を求めたり,因子分析の因子空間を求めたりするだけでなく,個人差を記述するモデルを想定することができる.INDSCALなどでは,次元のウェイトに個人差を反映させるので,次元に対する弁別のよさや識別のウェイトの違いに個人差を表現している.3相因子分析やその前身であるPOVモデルでは,刺激空間や尺度空間とは別に個人差空間を仮定している.通常の因子分析などは,因子構造を共通にして,因子に対する量的差異によって個人差を表現する.刺激と評価者との類似度から同時に空間に表現する展開法関係の分析(展開法,外部展開法,コレスポンデンス分析などの積和の分析法など)も片方の要素(相)が人間であるときには個人差分析の方法と言える.
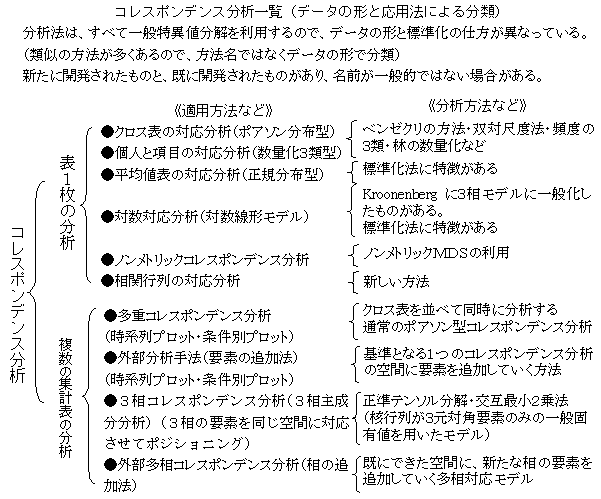
コレスポンデンス分析(correspondence analysis,対応分析)
集計表から、列要素(項目など)と行要素(評価対象など)を空間的にマッピングして、近さ遠さの対応関係を見る方法として、広く利用されている。
評価対象と評価項目を同一空間内に表現することは、因子分析や主成分分析なども用いられ、計算法も似ている部分が多い。コレスポンデンス分析の手順は、①分析前のデータの原点を行や列の主効果を除く位置に移動すること、②主成分分析と同じように固有値・固有ベクトルによって少ない次元で近似すること、③列要素と行要素が対応するように標準化して結果をプロットすること、の3つの段階になる。コレスポンデンス分析の特徴は、手順①の部分とそれに対応した手順③の部分にあることから、分析結果が空間内での距離の近さ遠さとして理解できる点にある。
コレスポンデンス分析は、クロス集計表の分析法として提唱されたが、上記のような原理に従えば、形式的に、横%表、平均値表などにも適用することができる。また、因子分析の因子得点のみを計算するのと同じように、既に分析された固有値・固有ベクトルを用いて、行要素や列要素の得点のみを計算することも可能である(列要素・行要素の追加法、Benzecri,1992)。さらに、最初に分析した相(評価対象など)と新しい相(嗜好度など)との関係を表した集計表から、新しい相(嗜好度など)を空間内に追加することも可能である(相の追加法、君山、2005)。そのほか、2元表のデータから3元表のデータに一般化して、3つの相の要素を同じ空間にプロットする3相コレスポンデンス分析も考えられている。
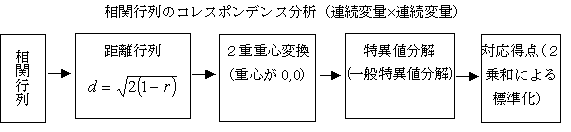
コレスポンデンス分析(相関行列の対応分析)
相関行列のコレスポンデンス分析は、連続変量群と連続変量群との関連性を分析する方法である。カテゴリー×カテゴリーが通常のコレスポンデンス分析、カテゴリー×連続変量が平均値表のコレスポンデンス分析である。正準相関分析に対応する分析法であるが、正準相関分析が、個別データサンプル得点の対応関係を目的にしているが、相関行列のコレスポンデンス分析は、変数の得点の対応関係を目的にしている点が異なっている。
分析の仕方は、図のように、相関行列を距離行列に変換し、2重重心変換を行い、特異値分解する。分散共分散行列、積和行列も同様に解くことができる。
正準相関分析はサンプル得点の合成変量の対応得点(正準得点)を求めることが目的であるが、ここでの相関行列の分析は、変数の得点を対応させているので、結果が異なる。また、シェーネマンの計量的展開法と目的は同じであるが、シェーネマンの展開法は、原点や得点の尺度値について、同一空間を求めようとしているが、ここでの分析法は、それぞれの尺度値の標準得点を対応されている(変数得点の相関係数最大化)。正準相関分析、シェーネマンの計量的展開法、相関行列のコレスポンデンス分析は、行要素と列要素の変数群が異なっている場合の、変数群間の関連性の次元軸(一種の主成分分析)を求める方法であるが、これらの方法は、異なった方法であると言える。
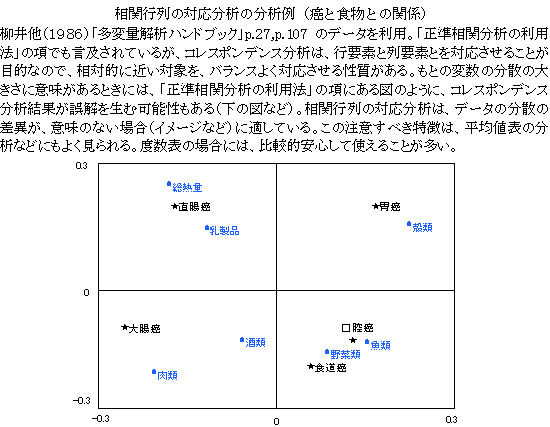
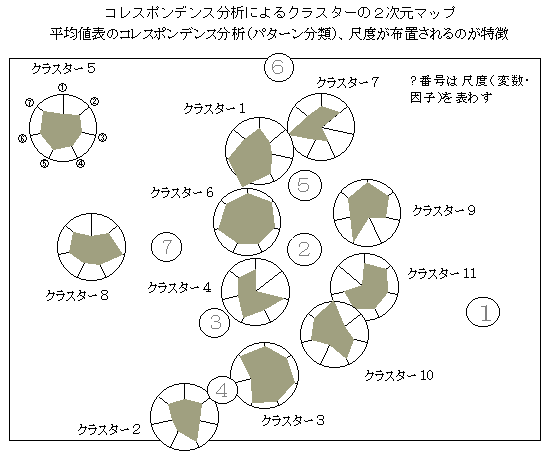
コレスポンデンス分析(平均値表の分析)
度数を表わす01データの2乗和は、合計と同じ値になるので、クロス表の標準化には、偏差計算の原点と分散調整の基準値は、理論度数として同じ値が用いられる(カイ2乗検定の理論度数、ポアソン分布の平均と分散)。平均値表の場合には、クロス表のようにゼロ点が事前に決まらないので、全体の平均値がゼロ点になり、測定値には正規分布が想定される(正規分布型)。したがって、コレスポンデンス分析のデータの標準化には、原点としては、分散分析と同じように行と列の平均値、全体の平均値が用いられ、単位調整の分母には、ゼロ点(全体平均)からの偏差2乗和が用いられる。このような操作は、その意味が、クロス表と全く同じになり、標準形への変換にも対応する。次元の縮小(2次元の近似)は、クロス表と同じように特異値分解がなされる。分析結果の行と列との対応関係は、偏差2乗和の平均値の平方根が用いられ、これは、データの標準化の数値と同じであり、一般化特異値分解の考え方からも矛盾しない。(「コレスポンデンス分析の利用法」参照。)

コレスポンデンス分析と双対尺度法・数量化3類との関係→「数量化3類・コレスポンデンス分析・双対尺度法」参照.
コンコーダンス
単語の文脈的な意味.言葉は,一般的な意味を持っているが,人間の行動を予測することを前提にして,言葉の意味を考えると,同一の言葉でも様々なメッセージを含んでいる.そこで、文脈を考慮して,言葉の意味や言葉の連鎖を捉えると、文章の意味は,単語ではなく,文脈を考慮することによって明確になる.文脈を考慮した言葉の種類は膨大な数になるが,意味を重視した比較的少数のコンコーダンスによって,文章を集計すると、文章の特徴が自動的に把握される.文章データを集計すると言うよりは,集計する意味要素(コンコーダンス)の構造をどのように定めるかという意味の把握モデルを決めることが最も重要なことになる.「文章意味集計システム」参照.
コンジョイント分析(conjoint analysis)
コンジョイント分析の特徴は,製品などの全体ではなく,構成要素を測定する点にある.評価は全体像であるが,推定すべき対象は構成要素である.この点は,分散分析と同じである.評価対象全体は,構成要因(属性)の統合として考えている.ゆえに,便利な点は,構成要因の内容を一部分変更するときなど,実際の製品全体の評価が分らなくても,要素が分っていれば,全体の評価を推定することができる.したがって,コンジョイント分析の最大の利点は,新製品のシェア予測などのシミュレーション予測にある.分析法としては,要因分析法(実験計画法)と同じであるが,応用の仕方として,幾つかの独自な特徴を持っている.①調査において,回答者一人一人推定ができるように,簡単で完備された計画が必要である.②簡単に測定ができるように,順序評価は中心に行われる(目的変数が順序データの要因分析法)③シミュレーションが目的なので,調査サンプルが母集団を代表する必要がある.(シェア推定のために多数のサンプルが必要).④そのほか,客観的に自動的に簡単に評価できるように,測定法が工夫されている.要因効果の測定法として,ペアワイズ法(トレードオフ法)とフルプロファイル法とがある.分析方法は,ノンメトリックな要因分析法であるノンメトリックカテゴリカル重回帰分析法が用いられるほか,累積ロジスティックモデルなどの順序データの分析法が用いられる.ノンメトリック(順序処理)の部分をはずすと,カテゴリカル重回帰分析になり,一般的な分散分析法,数量化1類などと同じ分析法になる.参考資料「A-58コンジョイント分析」5000円。
コンジョイントシミュレーション
コンジョイント分析結果を用いたシミュレーション.多数の調査サンプルのコンジョイントウェイト(ユーティリティスコア)から,個々人別々に複数の製品を,コンピュータシミュレーションとして選択させ,製品の選ばれた割合を集計する.製品の構成要素を変えながら,シェアの変化を見て,製造コストと売れ行きを見ながら,販売製品を決定する.本質的に,01型の重回帰分析,数量化1類,分散分析を個人レベルで適用した形になる.参考資料「A-58コンジョイント分析」5000円。
ゴンペルツ曲線
単調増加を表現する成長関数の一種.漸近線をy=1とすると,y=exp{-exp(1-λx)}のように表現できる.行動の記述としては,同じような形の関数であるロジスティック関数を用いることが多い.
Home 既刊書籍 会社概要 ア行 カ行 サ行 タ行 ナ行 ハ行 マ行 ヤ行 ラ行 ワ行 参考文献