|
1. 多層パーセプトロン 2. ニューロン 3. 何ができるのか？ 4. 学習機能 5. バックプロパゲーション法 1. 多層パーセプトロン多層パーセプトロン (Multi-Layer Perceptron : MLP) は、複数の層にニューロンを配置させた フィードフォワード型ニューラルネットワークです。 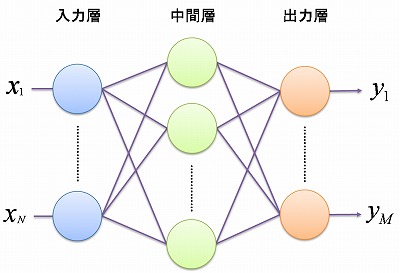 ニューロン（図では丸）を層状に並べたもの 2. ニューロンごく簡単に言えば、実際の生物のニューロンは、 自分につながっているニューロンから 受け取った電気信号の総和が あるしきい値を超えると、 他のニューロンへ電気信号を発します （これを発火といいます）。 これを模した ニューロンのモデルが次のようなものです。 N個のニューロンから信号を受け取るとします。 この信号を、ニューロンへの入力と呼び、
また、シナプスの伝達効率の良さにあたるものを結合重みと呼び、
さきほど述べたニューロンの性質を 簡単にモデル化したものが、 「入力と結合重みの積をすべて足し合わせたもの
大きくなければ発火しない」 というモデルです。 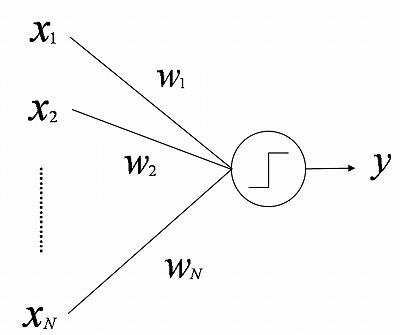 すなわち、ニューロンの出力を y とすると、
このモデルは McCulloch-Pitts モデルと呼ばれています。 （McCulloch さんと Pitts さんが提案したのです。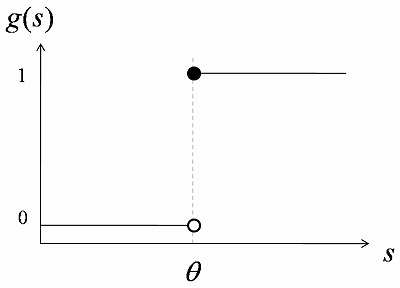）  この関数 g(s) は s = 0 で不連続なので、 微分できません。 後ほど紹介する結合重みの学習方法では ニューロンの関数が微分できる必要があるため、
（シグモイド sigmoid というのは 「S字型の」という意味です。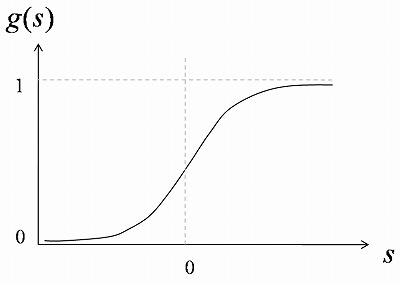）  多層パーセプトロンは このシグモイド関数を持つニューロンが 層状に配置されています。 （ただし、入力層のニューロンは 入力の値をそのまま出力します。） 各ニューロンへの入力は、 前の層の各ニューロンの出力の重み付き和となります。 出力層ニューロンの出力が、 多層パーセプトロン全体としての出力となります。 3. 何ができるのか？たとえば、ソフトコンピューティングのページでの例のように、 文字の画像を入力して それがどの文字であるかを出力する、 といったような、 入力と出力がどういう関係であるか？ ということを表現することのできるモデルです。 つまり、入力から出力への関数（写像）を 表わすことができるのです。 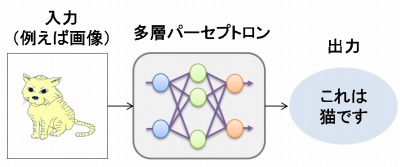 例えば画像から抽出した特徴量を入力すると その画像が何であるか判断して出力してくれる 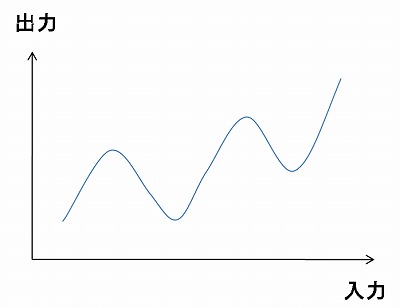 入力から出力への写像を表現する （非線形関数を近似できる） 結合重みを変更すると、 ニューロンのシグモイド関数の形が変わり、 ひいては多層パーセプトロンの関数の形が変わります。 つまり、結合重みをうまく調節することで、 いろんな形の関数を表現することが可能になります。 それも、多くのニューロンを使うほど、 多層パーセプトロンは あらゆる関数を表現できるようになります。 4. 学習機能入力値と出力値が対になったデータをもとにして結合重みを調節することで 入出力関係の学習を行うことができます。 「データをもとにして」 というのは、具体的には 「多層パーセプトロンの出力と データの出力値との 誤差を小さくするように」 ということになります。 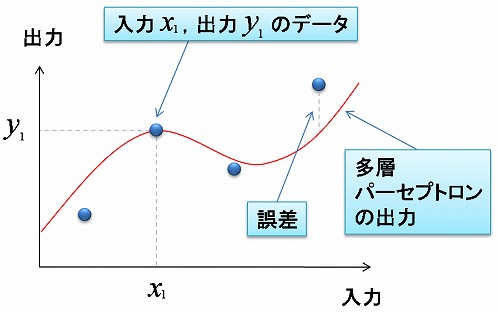 データとの誤差を小さくするように 結合重みを学習する 学習の方法として いちばんメジャーなものは、 バックプロパゲーション法です。 5. バックプロパゲーション法バックプロパゲーション法は、1986年に Rumelhart、Hinton、Williams によって 発表された学習方法です。 誤差関数をパラメータで微分することによって パラメータの修正方向を決めて パラメータの修正を繰り返すという勾配法を 多層パーセプトロン用に拡張したものです。 誤差を出力層から前の層へ伝搬していくことから バックプロパゲーション（Back Propagation : （誤差）逆伝搬）法 と名付けられています。 バックプロパゲーションのアルゴリズムについては 非常に多くの解説が 教科書やウェブ上にありますので、 ここでは詳しく解説しません。 原理もアルゴリズムも そんなに難しいものではないです。 プログラムにするのは 少しややこしいかもしれませんが。 次のページでは 3層パーセプトロンのバックプロパゲーションを シミュレーションするJavaアプレットをお見せします。 |