鉄道模型おきらく研究室:レイアウトと列車のページ
牽引力の簡易計測
(2003/11/4追記)
はじめに
牽引力は静摩擦係数×重量で決まることが牽引力の基礎理論で分かりました.そこで,手元にある車両を測定してみました.なお,厳密には,動摩擦係数(粘着係数)を求めるべきです.このコンテンツ作成後に実験した例では,動摩擦係数(粘着係数)を求めています.したがって,このコンテンツの実験結果は参考扱いとしてください.
計測車両
下表の9台です.
表 供試車両(順不同)
|
車種
|
画像
|
メーカー
|
備考
|
|
EF58 |
 |
KATO |
|
|
EF64−1000 |
 |
KATO |
|
|
EF64−1010 |
 |
TOMIX |
|
|
EF66−100 |
 |
TOMIX |
|
|
DD51 |
 |
KATO |
|
|
DD54 |
 |
KATO |
|
|
DE10 |
 |
TOMIX |
非対称(ゴム輪は2軸台車側のみ) |
C55流改九州型
(テンダーのみ) |
 |
ワールド工芸 |
非対称(8輪中,ゴム輪は1輪のみ) |
|
D51−78 |
 |
MICROACE |
非対象(ゴム輪第4動輪のみ) |
|
測定方法
摩擦係数(粘着係数):傾斜法
レールの上に車両を乗せ,線路(篠原のコンクリート枕木のフレキシブル線路を板に固定したもの( こちらの画像 の右側です)を傾けます.どんどん傾けていくと滑り出します.このときの角度をα求めます.
摩擦係数μは
μ=Tan α
で表せます.
試験は,車両の前を持ち上げるのを2回,後ろを持ち上げるのを2回の合計4回繰り返しました.その結果から平均値と標準偏差を求めました.なお,前後非対称の構造の車両(D51,DE10,C55)は標準偏差を求めていません.これは,偶然誤差ではなく偏り誤差(必然的な誤差)だからです.
車両重量:ばね計りで計りました.試験は1回だけです.計りのヒステリシスで3gぐらいの誤差がありそうなので,標準偏差を一律3gとしました.
測定結果
下図のようになりました.縦軸は摩擦係数(粘着係数)で縦軸は重量です.重量×摩擦係数(粘着係数)が牽引力になります.牽引力一定の線が青い線です.マーカーは測定結果の平均値です.マーカーの十字は,標準偏差をあらわしています.図中の矢印は,誤差(標準偏差)の大きさを表します.たとえば,平均値ではDD51のほうがEF66よりも牽引力は大きいのですが,誤差を考えると,牽引力の範囲ほとんど重なります.したがって,これら2両には牽引力の明らかな差はありません.でも,これらの機関車とEF58とでは矢印は重ならないので,明らかに牽引力が違います.
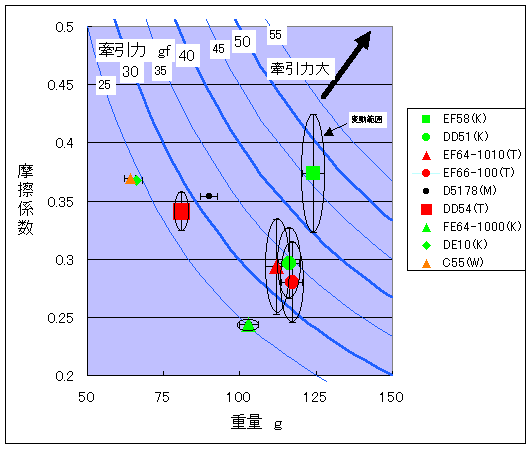
図 牽引力の推定結果
(静摩擦係数からの推定につき,参考データ)
|
考察
EF58では駆動力の変動範囲(標準偏差)が±5gぐらいあります.したがって,誤差を上回る差(有意差)を検出するには牽引力の差が10gf以上必要です.逆にいえば,10gf以下の差は気にしてもしかたありません.したがって,25gf級,35gf級,45gf級の3階級ぐらいのクラスに分類することが妥当だと思います.
摩擦係数(粘着係数)は0.24〜0.37ぐらいに分布しています.摩擦係数(粘着係数)の標準は最大0.05ぐらいですから,0.05単位で丸めると,摩擦係数の平均値は0.3ぐらいと見てよいと思います.したがって,大雑把には
牽引力=0.3×重量
と考えられます(誤差は5gfぐらいあります).
2003/11/4追記
現在,新幹線電車(実物)で用いられている粘着係数の式は文献(1)によれば
粘着係数μ=27.2/(V+85)
だそうです(鉄道技術研究所:高速鉄道の研究,研友社(1967)).ここでVは速度(km/h)です.
このコンテンツでは発進時,すなわちV=0を扱っているので,上の式にV=0を代入すると
μ=0.16
になります.この値は,図1にくらべると小さいですね.模型にはゴム輪がついているおかげでしょうか.
文献(1)自動車技術Vol.57No.10,2003,P52鉄道車両の空転・滑走とその制御,渡邉朝紀
|
今後
電車も測定してみたいと思います.


