鉄道模型おきらく研究室:レイアウトと列車のページ

牽引力の基礎理論
おきらく研究 〜牽引力の研究:牽引力≒静摩擦力〜
0.はじめに
モデラーが力を合わせて牽引力を測定しようというプロジェクト があります.そこで,車輪の駆動力についてお気楽研究(というよりも文献調査)してみました.
1.基本的な考察
はいでは,牽引を
牽引力=(動力車とレールとの)静摩擦係数×重量
との関係で大雑把には表せると考えています.それは,モーターが最大トルクを出すと空転してしまうことがほとんどなので,モーターのトルクは生かしきれず,駆動力の限界が摩擦力で決まってしまうからです.
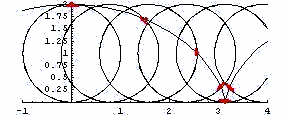
では,なぜ走行中は車輪が回転しているのに(冒頭で申し上げましたが)「静」摩擦なのでしょうか.そこで,下の図をご覧下さい.車輪のある一点(赤点)の軌跡を計算した結果です(車輪は45度回転ごとにプロットしました).なお,縦軸,横軸とも目盛1が半径を表しています.
赤点がレールに接触するときは,ハンコをおすように上から押し付けられ,上に離れていくことがわかります(接触前後の45度回転で,x方向に半径の10%ぐらいしか進んでいないことにご注目下さい).従って,回転中の車輪といえども,レールと接触している瞬間は止まっています.ですから,静摩擦係数で回転中のタイヤの摩擦係数(粘着係数)を表せると考えています.
ご参考:計算法
余談ですが,上の図の軌跡はサイクロイドと呼ぶらしいのです.計算式を記載しておきます.
上下方向の座標をz,前後方向の座標をx,車輪の回転角をα,車輪の半径をRとすると
z=R(1+Cos α)
x=Rα+Sinα
です.興味の有る方はEXCELで計算されてみてはいかがですか.
2.摩擦係数の考え方を文献で調べてみました.
鉄道総研月例発表会講演要 旨:摩擦ブレーキトルク推定とフィードバック制御への適用,車両制御技術研究部ブレーキ制御副主任研究員山崎大生 先生の論文(http://www.rtri.or.jp/infoce/getsurei/2002/Getsu06/g150_5.pdf でごらんになれます)の図1をご覧下さい.車輪の力を大雑把にモデル化されています.図1の縦軸のフラットな部分μmaxが静摩擦係数と思われます.と言いますのは横軸λの絶対値が5%よりも大きくなると(スリップが大きいほど)μが小さくなりますが,これが動摩擦係数(粘着係数)だと思われるからです(静摩擦係数>動摩擦係数(粘着係数)なので).このように,すべりの小さい領域における車輪の発生する力の限界を静摩擦係数とみなしている研究者がいることがわかりました.
なお,横軸λは山崎先生の式(3)に書いてあるようにスリップ率だそうです.式(3)を解釈すると,スリップ率とは,車輪とレールとの相対速度を車速で割った値です.たとえば,車輪の周上の速度が時速60Kmで車体の速度が時速50kmなら,車輪とレールとの相対速度(滑っている速度)は時速10kmになります.一方,車体の速度が時速50kmなので,λ=10/50=0.2となります.つまり,車体の速度の0.2倍の速度ですべっていることを表しています.(ただ,はいでの私見として,完全に滑っているときのλに本質的な意味はないように思います.動摩擦係数(粘着係数)は車輪とレールとの相対速度だけで決まるはずで,車体の速度は関係ないと考えるからです.)
このように,スリップ率が小いときは摩擦係数の最大値は静摩擦係数であらわすことがある――――――ことがわかりました.
3.ゴムタイヤの摩擦係数の測定例を調べてみました.
下記URLに,横浜国大の吉本貫太郎さんが計測された,ゴムタイヤとレールとの摩擦係数がプロットされています.
(http://www.kawalab.dnj.ynu.ac.jp/~kanta/train/train.html をご覧下さい)
この例結果は,上に凸なので,先の山崎先生の図1に似ています.違うのは,静摩擦領域が明確には現れていない(狭い)ことと,鉄道車輪に比べて,動摩擦係数の速度依存性が小さいことです.スリップ率100%で,鉄道車輪(鉄輪)では動摩擦係数が静摩擦の50%ぐらいの低下を想定していましたが,ゴムタイヤでは目測30%ぐらいの低下です.
この結果からは,「スリップ率が小いときは摩擦係数の最大値は静摩擦係数である」ことは言えませんでした.そこで,この吉本さんの図をもう少し解釈してみます.
4.自動車用タイヤの文献を調べてみました
ゴムタイヤの性質を調べるために,自動車のタイヤを調べてみました.
(株式会社)豊田中央研究所のHPにスリップ率とタイヤ発生力(垂直荷重で割れば摩擦係数となり,山崎先生の図1の縦軸と同じになります)との実測例が記載されています(http://www.tytlabs.co.jp/office/library/lib_01/taiyaundou.pdfの左下の図です).この図から,
鉄道のゴムタイヤも,自動車のゴムタイヤもだいたい同じ性質を持っていることが分かりました.
では,タイヤの力が最大の点は,静摩擦なのかどうかを調べてみます.タイヤの理論解析モデルを調べると「FIALAモデル」というものがありました.この概念図(http://www.nozomi.iis.u-tokyo.ac.jp/exhibition/tire.pdf の2ページ目,上に○3と書いているページの図です).タイヤ発生力の式はhttp://www.ynl.t.u-tokyo.ac.jp/publications/papers96/theses/yuji/main.htmlの式(4)です.この式は3次関数なので,上に凸になります.はいでの計算によると,この曲線のピーク値はμです(ちなみに,そのときのスリップ率は3μW/2Kです).μとは摩擦係数です.導出過程を読むとタイヤのゴムが変形したときに,滑り始める条件(滑り速度0)でμを定義していますので,μとは静摩擦係数のことです. したがって,FIALAモデルによると,吉本さんの図のピークは静摩擦と考えることができます.
なお,この式は前後力(制動・駆動力)ではなくて横力(旋回する力)を計算している(そのため,スリップ率ではなくてスリップ角となっています)ようですが,剛性Ky(ゴムの横剛性)を前後剛性と読み替えても成立します.
5.計算例
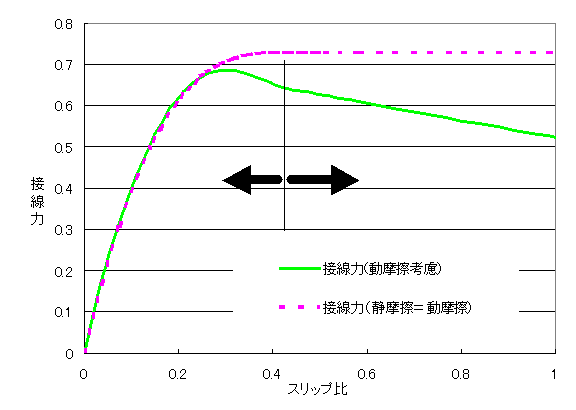
Fialaモデルに「摩擦係数の滑り速度(スリップ比)依存性」を考慮して計算してみました.下の図をご覧下さい.
緑の線は大石研究室の測定結果(http://hp73.nagaokaut.ac.jp/research/rail/traction.html )にだいたい合うように最大静摩擦係数(約0.7@スリップ率0.2)と動摩擦係数のスリップ比依存係数(摩擦係数0.5@スリップ率1)を決めたものです.赤の線は,「動摩擦係数のスリップ比依存係数=0」すなわち「動摩擦係数=静摩擦係数」として計算した結果です.駆動力(接線力)は静摩擦よりも5%ぐらい小さくなるようです.したがって, おおざっぱには
駆動力=0.95×静摩擦係数
ぐらいです.
したがって,
牽引力=(動力車とレールとの) 静摩擦係数× 0.95 × 重量
となります.
もし,5%(消費税率と同じです)を気にしないのであれば,冒頭の式と同じになります.
6.まとめ
牽引力は,大雑把には静摩擦力,すなわち摩擦係数と重量とできまりそうです.今度は,実測してみようかと思います.
7.ご参考
スリップ率の説明は,下記URLでわかりやすく説明されています.
http://homepage1.nifty.com/Kart-Monkeys-Cage/fun_to_race/riron/5/riron_5.htm
ゴムタイヤのモデル化の例,下記URLの図6にあります.静摩擦=動摩擦としてるようです.
http://www.tytlabs.co.jp/office/library/review/rev343pdf/343_047hattori.pdf
スリップ比と接線力係数の図に,粘着領域と滑り領域が記されています.
http://hp73.nagaokaut.ac.jp/research/rail/traction.html
かなり余談ですが,ゴムの材質と摩擦係数との関係があります.シリカとやらを入れると摩擦係数が増えるそうです.
http://www.toyo-tire.com/mailmaga/backno_09/tirekun/tirekun_09.html
スリップ率と駆動力との関係
http://www.jari.or.jp/ja/kuruma/kuruma52/4wd1.html
http://www.ysm.co.jp/literature.htm
氷とゴムとの摩擦力の関係
http://www.techno-qanda.net/dsweb/Get/Document-3300/%CE%BC%E3%83%BC%EF%BD%93%E7%89%B9%E6%80%A7.doc
http://www.techno-qanda.net/dsweb/GetRendition/Document-3300/html/index.html
タイヤの数学モデル
http://www.geocities.co.jp/MotorCity-Circuit/3632/f1/tire.html

鉄道模型おきらく研究室:レイアウトと列車のページ