|
【 振動数 ： 音の高さを決める 】 音は、空気の振動です。 振動とは、波のことです。 波とは、媒質の変位が周期的に規則正しく変化する現象です。 この周期的な変化が、一秒間に起こる数を、振動数といいます。 振動数の単位は、[Hz]（ヘルツ）です。 ラジオの周波数とかと一緒です（ラジオの場合は電磁波の振動数。）。 さらに、最大の変位を振幅といいます。 この振動数が高いほど、音は高くなります。 （また、振幅が大きいほど、音は大きくなります。） 振動数が倍になると、1オクターブ高い音になります。 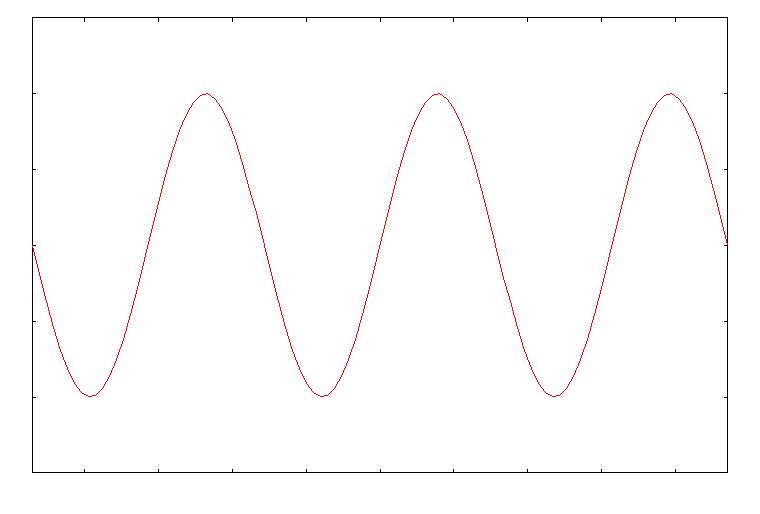 図1 低くて大きい音 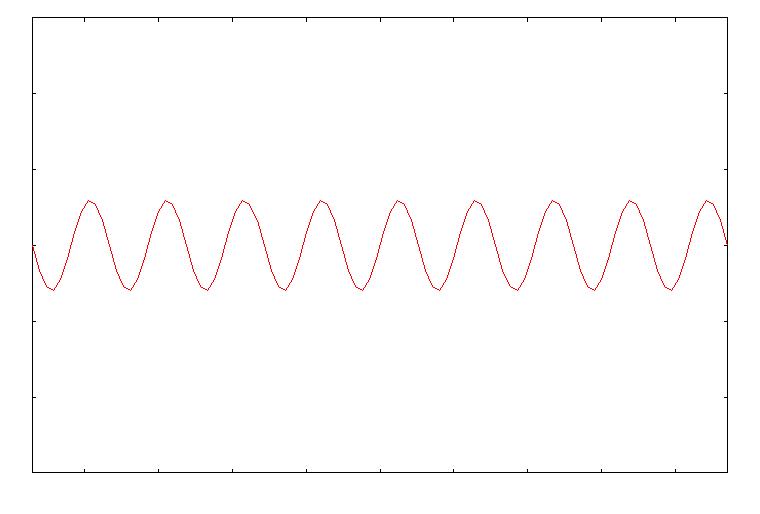 図2 高くて小さい音 さて、ある音があって、 この音の振動数は何Hzだろうと疑問に思ったとします。 そのためには、ある基準の音を決めないといけません。 そこで、基準として、440Hzの音を「A」としましょう。 （441Hzや442HzなどをAとするときもあるが、この説明では440Hzとする） このとき、1オクターブ上のAは880Hzです。 振動数が倍になると1オクターブ上の音になるのです。 さらに1オクターブ上のAは1760Hzですし、 基準のAより1オクターブ下のAは220Hzということになります。 Aのオクターブ上や下は、440を倍や半分にしていくだけなのですぐわかります。 じゃあ、他の「B」とか「bE」とか「bA」などの音は何Hzでしょう？ 例えば「bE」は、Aとそのオクターブ上のAのちょうど真ん中の音です。 では、bEは440と880の真ん中、660Hzでしょうか？ これはまちがいですね。 オクターブの間隔で振動数は倍倍で増えていきますから、 それぞれ半音は、振動数においては同じ間隔ではないのです。 では、各音の振動数はどうなっているでしょう？ まず、基準の440HzのAを「0（ゼロ）」と数字におきかえてみます。 1オクターブ上のAは「1」、2オクターブ上のAは「2」、 1オクターブ下のAは「-1」、といった具合です。 このように、音名を変数 x とします。 たとえば基準Aのすぐ上のbEは、x＝0.5です。 さて、このようにすると、 x＝-1 のとき 220＝440×(1/2) ＝440×{2^(-1)} Hz、 x＝0 のとき 440＝440×1 ＝440×(2^0) Hz、 x＝1 のとき 880＝440×2 ＝440×(2^1) Hz、 x＝2 のとき 1760＝440×4 ＝440×(2^2) Hz、 ということになります。（2^1 : 2の1乗） つまり、ある音 x は、440×(2^x) Hz であると言えそうです。 ここで、ある音 x に対して、1オクターブ高い音は（x＋1）です。 x が 440×(2^x) Hz だとすると、 （x＋1）は 440×(2^(x+1))＝440×{(2^x)×(2^1)}＝2×440×(2^x) Hz となり、 x の2倍になっています。 ということで、440HzのAを x＝0 とすると、 任意の音 x の振動数は 440×(2^x) Hz となります。 これにあてはめると、さきほどのbEは、 440×(2^0.5)＝622.2539…… となり、およそ622.3 Hz ということがわかります。 念のためその1オクターブ上のbEを調べましょう。 440×(2^1.5)＝1244.5079……となり、ちょうど2倍になっています。 これで、音程の最小単位を半音としたときはもちろんのこと、 半音よりも細かく音を区切っても、振動数が計算できます。 ちなみに、基準のAを441 Hz とすれば、 任意の音 x は 441×(2^x) Hz となることになります。 （スマートに言えば、音程というのは「振動数比」のことです。 それに関連して、「平均律」とか「純正律」とか そういう話もしたいところですが割愛します） 【 倍音 ： 音色を決める 】 楽器っていろいろありますよね。 で、音色がそれぞれ違います。 それではいったい何が音色を決めているのでしょうか。 例えば、ピアノの鍵盤をピンと弾いたとしましょう。 基準のAの音を弾いたとします。 上で見たように、このときのAの音は440Hz です。 ……と言いたいところですが、正確には正しくないのです。 このAの音の基本となる振動数は、たしかに440Hzです。 しかし、このとき、440Hz の2倍、3倍、4倍、……・と、 440Hz の整数倍の振動数の波も同時に発生して、鳴っているのです。 この、整数倍の振動数の音を「倍音」といいます。 順に、第2倍音、第3倍音、……と呼びます。 つまり、このAの音は、440、880、1320、1760、2200、……Hz の音が 合わさった音なのです。 音色の正体は、この「倍音の含まれ方の違い」なのです。 どういうことかというと、 違う楽器で同じAの音を鳴らしても、 この楽器は第3倍音が強く含まれているとか、 この楽器は第2倍音と第5倍音が比較的強く含まれているとかいうように、 各倍音の含まれ方が、楽器によって異なるのです。 これが、音色の違いとなるのです。 物理学的に言えば、波は「重ね合わせ」られます。 波と波は足し算ができるのです。 基本の波に各倍音の波を重ね合わせることで、 おのおのの楽器からでる音波は独自の波の形をもちます。 よって、音色の違いは波形の違い、ともいえます。 図3 基本の波形 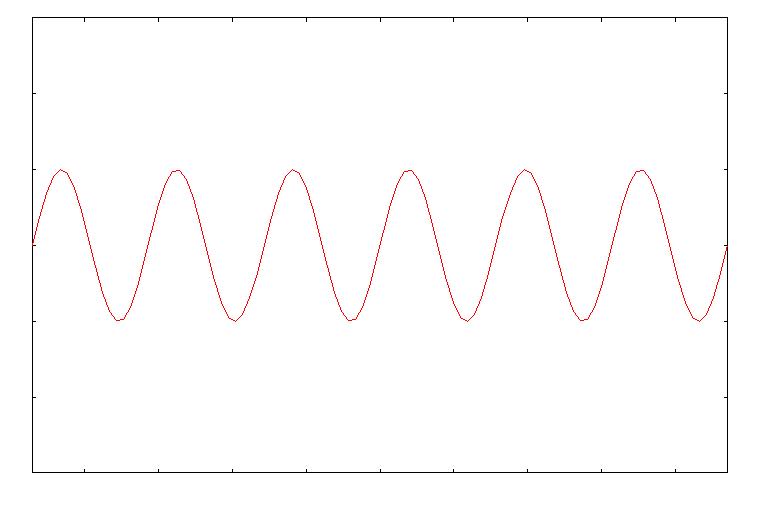 図4 図3の2倍の振動数の波形（弱め） 図5 図3の3倍の振動数の波形（もっと弱め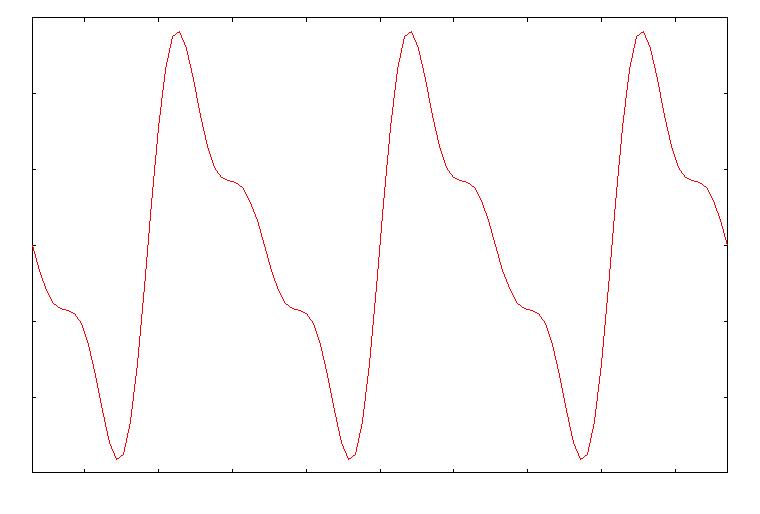）  図6 図3、4、5を重ね合わせた波形 楽器の種類（弦楽器とか管楽器とか）や楽器の形という、 楽器の構造上の違いが、倍音の生じ方の違いの原因でしょう。 こうして科学的に分析してみると、実に音は複雑なもんです。 |