|
1. RBFネットワーク 2. RBF？ 3. RBFの重み付き和 4. RBFネットワークの学習 1. RBFネットワークRBFネットワークは、3層からなるフィードフォワード型ニューラルネットワークです。 多層パーセプトロンと同様に、 任意の非線形関数を近似することができます。 2. RBF？RBFとは、Radial Basis Functionの略です。 日本語では、 動径基底関数とか放射状基底関数などと言われます。 これは、入力空間において 局所的に反応するような関数です。 つまり、中心で最大値（あるいは最小値）を取り、 そこから離れるにしたがって 単調に減少（あるいは増加）していくような関数です。 そのような関数はいろいろと考えられますが、 最もよく使用されるものが次のガウス関数です。
（ベクトル表記です。Tはベクトルの転置です。） σはガウス関数の標準偏差で、幅を決めるパラメータです。 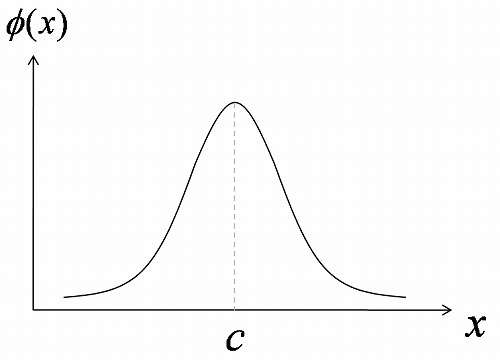 3. RBFの重み付き和RBFネットワークは、この基底関数の重み付き和によって 非線形関数を表現します。 N 個の基底関数 φi (i = 1, 2, ..., N) からなる RBFネットワークの出力 y は、 結合重みを wi として、
w0 はバイアスの値（y方向へのずれ）です。 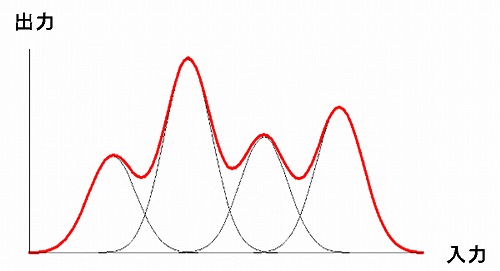 4. RBFネットワークの学習基底関数の中心、幅、結合重みを変更することでRBFネットワークの形は変化します。 データをもとにして、 つまりデータとRBFネットワークの出力との 誤差が小さくなるように 適切なパラメータを推定するのが RBFネットワークの学習です。 これらは勾配法によって学習することもできますが、 基底関数の中心と幅を適当に決めてやれば （データの入力分布をもとに決めるなど）、 結合重みを最小二乗法によって 一発で求めることができます。 |