補足:3次関数による緩和曲線の導出過程
ここでは,3次関数による緩和曲線の導出過程のご説明をいたしますが,正直言って,あまり説明が丁寧ではなく,私の忘備メモに近いのが現状です.とりあえず,中ほどの曲率(半径の逆数)の図(横軸:直線の延長の位置,縦軸:曲率)を見ていただければ,よろしいかと存じます.将来的には高校生の皆さんにも理解できるようにしたいものです.
第1段階 緩和曲線長さの誘導
まず,座標系を決めます.水平方向にx軸を,鉛直方向にy軸をとり,それぞれ右,上を正の向きとします.直線区間は水平で左から右に走り,原点で左旋回するものとします.
そこで緩和曲線を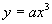 ――――――(1)
――――――(1)
とおきます.これをベクトル表示して,緩和曲線の位置ベクトルを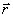 とすると,
とすると,
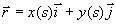 ――――――(2)
――――――(2)
とかけます.ここで,sは原点からの緩和曲線ぞいの長さ,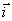 はx方向の単位ベクトル,
はx方向の単位ベクトル,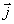 はy方向の単位ベクトルです.
はy方向の単位ベクトルです.
さて,緩和曲線上の微小長さdsは,三辺法の定理から
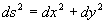 ――――――(3)
――――――(3)
です.したがって
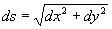 ――――――(4)
――――――(4)
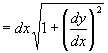 ――――――(5)
――――――(5)
ここで式(1)から
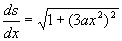 ――――――(6)
――――――(6)
となります.これで横方向の位置xを指定すれば曲線の長さsがもとまります.
第2段階 接線ベクトルの誘導
接線ベクトルを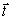 とします.
とします.
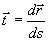 ――――――(7)
――――――(7)
ですが,いきなり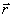 をsで微分できないので,xで微分すると
をsで微分できないので,xで微分すると
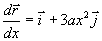 ――――――(8)
――――――(8)
となります.そこで,式(6),(8)を利用して
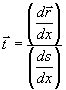
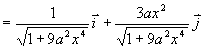
となります.
第3段階 曲率の誘導
曲率ベクトル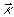 を求めます.なお,
を求めます.なお,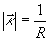 (R:半径)です.
(R:半径)です.
さて,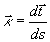 ――――――(9)
――――――(9)
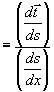
でもとめられます.そこで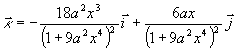 ――――――(10)
――――――(10)
となるので,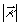 は
は
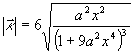 ――――――(11)
――――――(11)
となります.
ここで,気分をかえて,曲率(=1/半径)の絶対値のグラフをご覧下さい.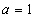 のグラフを下図に示します:横軸がx,縦軸が
のグラフを下図に示します:横軸がx,縦軸が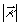 (=1/R)です.
(=1/R)です.
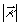
=1/R |
 |
|
位置 x
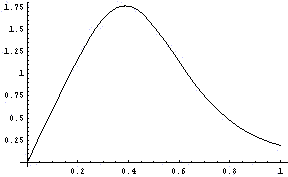
図1 3次曲線の曲率
|
このグラフの特徴は
1)x=0で曲率が0,つまり緩和曲線の始まりでは直線です.
2)xがある値(この場合x=0.4付近)で曲率が最大になる.しかも,この付近では曲率は変化しない,つまり円の一部(弧)が存在する.
そこで,上図の場合,x=0で直線に,x=0.4付近で曲率1.7(半径=1/1.7)の円にスムーズにつなげます.
第4段階 定数項aの決定
それでは,半径Roの円につなげるための定数項aもとめます.曲率が最大になるときのxをxoとすると,式(11)をxで微分したものを0とおくと求まり,
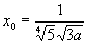 ――――――(12)
――――――(12)
のときです.そしてこのときの曲率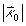 は
は
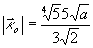 ――――――(13)
――――――(13)
です.ここで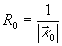 なので式(13)から
なので式(13)から
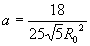
となります.このaを式(1)に代入することで,半径Roを指定したときの緩和曲線が求まります.
第5段階 緩和曲線と本来の曲線との接続
x=xoのときの緩和曲線の傾きは
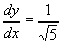
となるので,xoにおける緩和曲線とx軸とがなす角度pは
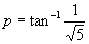 (rad)
(rad)
となります.これをdeg換算すると24.1°になります.したがって,Roにかかわらず,24.1deg向きを変えたところで半径一定の曲線に合流します.したがって,半径一定の円は24.1°のところで繋げばよいことがわかります.


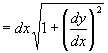 ――――――(5)
――――――(5)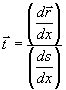
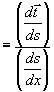
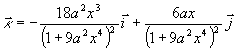 ――――――(10)
――――――(10)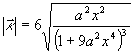 ――――――(11)
――――――(11)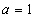 のグラフを下図に示します:横軸がx,縦軸が
のグラフを下図に示します:横軸がx,縦軸が
