EXCELによる数量化3類例題
主成分分析の例題を使用し、数量化3類の分析を実施する。ビジネスのカテゴリを削除し、それぞれのカテゴリで、該当あり:1 該当なし:0 の数量を与える。またカテゴリ反応数、アイテム反応数を求めておく。
|
|
ニュース |
スポーツ |
|
||
|
|
充実 |
不充実 |
充実 |
不充実 |
カテゴリ |
|
NO |
X11 |
X12 |
X31 |
X32 |
反応数 |
|
1 |
1 |
0 |
0 |
1 |
2 |
|
2 |
0 |
1 |
1 |
0 |
2 |
|
3 |
1 |
0 |
1 |
0 |
2 |
|
4 |
0 |
1 |
0 |
1 |
2 |
|
5 |
1 |
0 |
1 |
0 |
2 |
|
6 |
0 |
1 |
0 |
1 |
2 |
|
7 |
0 |
1 |
1 |
0 |
2 |
|
8 |
1 |
0 |
0 |
1 |
2 |
|
9 |
0 |
1 |
0 |
1 |
2 |
|
10 |
1 |
0 |
1 |
0 |
2 |
|
サンプル反応数 |
5 |
5 |
5 |
5 |
|
1. カテゴリスコア・サンプルスコアを求める。

とする。
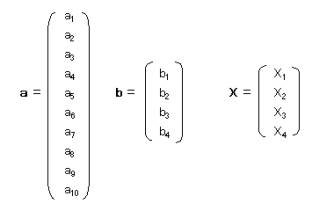 また
また
とする。aはサンプルスコア、bはカテゴリスコア、Xは固有ベクトルを求めるため行列である。

これより
λ2=0、1、0.6 0.4 λ2=0、1は無意味なので、λ2=0.6 0.4を採用する。
1.1 λ2=0.6 の時

X1=0.5 X2=−0.5 X3=0.5 X4=−0.5
1.1.1 カテゴリスコアを求める。
b = B-1/2・Xより

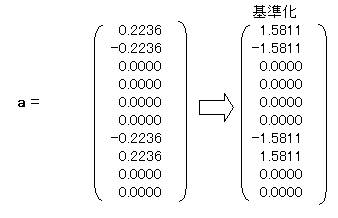
求められたカテゴリスコアを更にその標準偏差で割って基準化すると
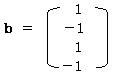
1.1.2 サンプルスコアを求める。
![]()
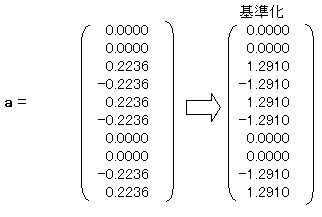
1.2 λ2=0.4 の時

X1=0.5 X2=−0.5 X3=−0.5 X4=0.5
1.2.1 カテゴリスコアを求める。
b = B-1/2・Xより

求められたカテゴリスコアを更にその標準偏差で割って基準化すると
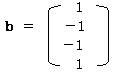
1.2.2 サンプルスコアを求める。
![]()
以上をまとめると
カテゴリスコア
|
λ2 |
ニュース |
スポーツ |
||
|
充実 |
不充実 |
充実 |
不充実 |
|
|
b11 |
b12 |
b31 |
b32 |
|
|
0.6 |
0.5 |
−0.5 |
0.5 |
−0.5 |
|
0.4 |
0.5 |
−0.5 |
−0.5 |
0.5 |
カテゴリスコアをグラフ化する
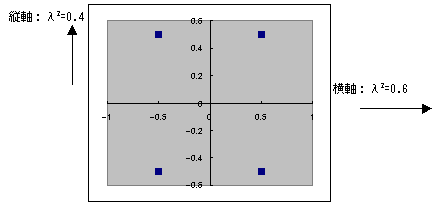
λ2=0.6を横軸に、λ2=0.4を縦軸にとりカテゴリスコアをグラフ化する。
これを見ると、横軸の+方向に紙面の充実度の程度、縦軸+方向に専門紙指向、−方向に大衆紙指向の度合いと考えられる。
次にサンプルスコアを同様にグラフ化する。
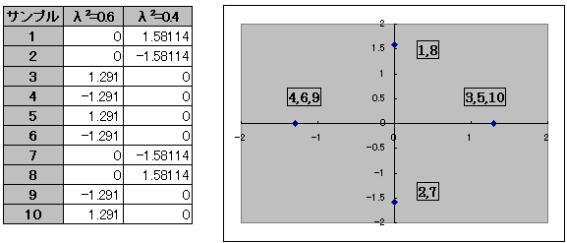
λ2=0.6を横軸に、λ2=0.4を縦軸にとりサンプルをグラフ化する。
横軸の+方向に紙面の充実度の程度、縦軸+方向に専門紙指向、−方向に大衆紙指向の度合いと考えられるので、紙面の充実度の高いのは、3,5,10の3紙であり、不充実の紙は4,6,9の3紙である。専門紙志向が強いのは、1,8の2紙であり、大衆紙志向の強いのは、2,7の2紙である。