EXCELによる数量化2類例題
判別分析の例題は、説明変量が量的データであり、目的変量が質的データであった。この表を元にして、説明変量において、6点以上を該当あり、5点以下を該当無しとして新しい表を作成する。この新しく作成された表はすべて質的データであるから、数量化2類の分析を実施する。
判別分析で使用した表
|
ＮＯ |
Ｘ1 礼儀 |
Ｘ2 積極性 |
Ｘ3 強調性 |
Ｘ4 業界区分 |
|
１ ２ ３ ４ ５ ６ ７ ８ |
３ ８ ６ ８ ７ ４ ６ ７ |
８ ２ ７ ６ ３ ７ ３ ５ |
４ ６ ６ ４ ５ ３ ６ ８ |
Ａ Ｂ Ａ Ａ Ｂ Ａ Ｂ Ｂ |
１． 数量化2類分析用に質的データの表にする。
6点以上を該当有り：「１」 5点以下を該当無し：「０」 A業界：「１」 B業界：「２」とする。
|
ＮＯ |
Ｘ1 礼儀 |
Ｘ2 積極性 |
Ｘ3 強調性 |
Y 業界区分 |
|||
|
|
有り |
無し |
有り |
無し |
有り |
無し |
|
|
１ ２ ３ ４ ５ ６ ７ ８ |
０ １ １ １ １ ０ １ １ |
１ ０ ０ ０ ０ １ ０ ０ |
１ ０ １ １ ０ １ ０ ０ |
０ １ ０ ０ １ ０ １ １ |
０ １ １ ０ ０ ０ １ １ |
１ ０ ０ １ １ １ ０ ０ |
１ ２ １ １ ２ １ ２ ２ |
新しく作成した表を見ると、説明変量X2と目的変量Yが1対1で対応状態となっている。このままでは変量X2さえあれば、他の変量はいらないということになるので、X2の変量を削除する。説明変量X1・X3と目的変量Yの表
|
|
礼儀： |
X1 |
協調性： |
X3 |
業界区分 |
|
|
有り |
無し |
有り |
無し |
|
|
標本 |
X11 |
X12 |
X31 |
X32 |
Y |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
0 |
2 |
|
3 |
1 |
0 |
1 |
0 |
1 |
|
4 |
1 |
0 |
0 |
1 |
1 |
|
5 |
1 |
0 |
0 |
1 |
2 |
|
6 |
0 |
1 |
0 |
1 |
1 |
|
7 |
1 |
0 |
1 |
0 |
2 |
|
8 |
1 |
0 |
1 |
0 |
2 |
上の表のデータを元にして数量化2類の分析を実施する。
X11･X31の成分を取り除き、業界区分をキーとして昇順にソートし、2群に分ける。
さらに各群の小計と2群の合計を求めると以下の様な表になる。
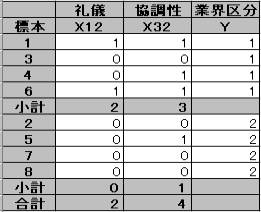
２． 上の表を元に線形判別式を求める。
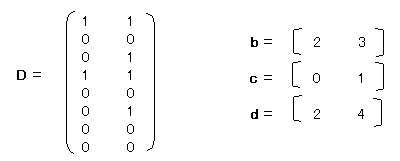
とすると
(0.25−η2 )･(0.125−η2)−0.25×0.125＝０
η2＝ 0，0.375
分散比（η2）は０で最小となり、0.375で最大となる。
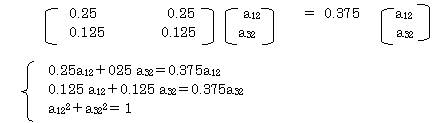
以上から a12 ＝ 0.894 a32 = 0.447
線形判別式は、Y＝ 0.894X12 ＋ 0.447X32
この式を基準化すると、Y＝ −0.2235X11＋0.6705X12−0.2235X31＋0.2235X32
この判別式を使用して予測値（Y')を求める。さらに求めた予測値の標準偏差を求め、各予測値を割って標準化（平均：０ 標準偏差：１）する。さらに標準化された予測値の各群の平均値を求める。
|
|
礼儀 |
|
協調性 |
|
業界区分 |
|
|
|
|
|
有り |
無し |
有り |
無し |
|
予測値 |
標準化 |
|
|
標本 |
X11 |
X12 |
X31 |
X32 |
Y |
Y' |
Y' |
各群平均 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0.894 |
1.52753 |
|
|
3 |
1 |
0 |
1 |
0 |
1 |
-0.447 |
-0.7638 |
|
|
4 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
6 |
0 |
1 |
0 |
1 |
1 |
0.894 |
1.52753 |
0.5728 |
|
2 |
1 |
0 |
1 |
0 |
2 |
-0.447 |
-0.7638 |
|
|
5 |
1 |
0 |
0 |
1 |
2 |
0 |
0 |
|
|
7 |
1 |
0 |
1 |
0 |
2 |
-0.447 |
-0.7638 |
|
|
8 |
1 |
0 |
1 |
0 |
2 |
-0.447 |
-0.7638 |
-0.573 |
|
|
|
|
|
|
平均 |
0 |
0 |
|
|
|
|
|
|
|
標準偏差 |
0.58526 |
1 |
|
以上から1群（A社）の重心：0.573 2群（B社）の重心：−0.573 である。
３．レンジ（範囲）を調べる。
各アイテムの各カテゴリを基準化して、最大値−最小値からレンジを求める。
|
|
礼儀 |
|
協調性 |
|
業界区分 |
|
|
有り |
無し |
有り |
無し |
|
|
標本 |
X11 |
X12 |
X31 |
X32 |
Y |
|
1 |
0 |
0.6705 |
0 |
0.2235 |
1 |
|
3 |
-0.2235 |
0 |
-0.2235 |
0 |
1 |
|
4 |
-0.2235 |
0 |
0 |
0.2235 |
1 |
|
6 |
0 |
0.6705 |
0 |
0.2235 |
1 |
|
2 |
-0.2235 |
0 |
-0.2235 |
0 |
2 |
|
5 |
-0.2235 |
0 |
0 |
0.2235 |
2 |
|
7 |
-0.2235 |
0 |
-0.2235 |
0 |
2 |
|
8 |
-0.2235 |
0 |
-0.2235 |
0 |
2 |
|
合計 |
-1.341 |
1.341 |
-0.894 |
0.894 |
|
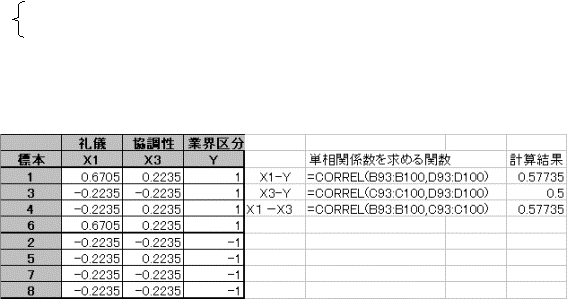アイテム1：0.6705−(−0.2235)＝0.894
アイテム２：0.2235−(−0.2235)＝0.447
アイテム1(礼儀)の方がレンジが大きい。よってアイテム1の方が外的基準に与える影響は大きい。
４．各アイテムと外的基準間の単相関係数を調べる。
B業界区分に数量−１を与える。
X1(礼儀)とYの単相関係数：0.57735 X2とYの単相関係数：0.5
X1の単相関係数が大きい。X1(礼儀)の方が外的基準に与える影響は大きい。
またX1-X3の単相関係数：0.57735であり、X1-X3間の多重共線性はないと考えられる。
５．偏相関係数を調べる。
相関係数行列を作成し、その逆行列を求める。
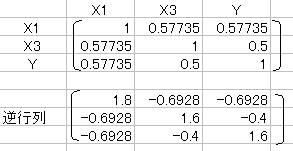
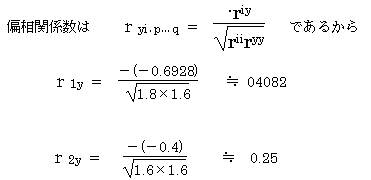
各アイテムと外的基準との偏相関係数も、X1−Yの方が大きい。X1(礼儀)の外的基準に与える影響の方が大きい。