EXCELによる数量化1類例題
重回帰分析の例題は、店員充実度・売場面積・商品充実度などが量的データであった。これをいま、6点以上を「良い」、5点以下を「悪い」と質的データにして、数量化1類の分析を行う。重回帰分析の例題を書き直すと下のような表となる。この表を元にして分析を実施。該当あり：１ 該当なし：０ とする。
|
ＮＯ |
アイテム1 店員充実度 |
アイテム2 売り場面積 |
アイテム3 商品充実度 |
売上高 （単位：百万円） |
|||
|
良いa11 |
悪い a12 |
良いa21 |
悪いa22 |
良い a31 |
悪い a32 |
Y |
|
|
１ ２ ３ ４ ５ ６ ７ ８ |
１ １ ０ ０ １ ０ ０ １ |
０ ０ １ １ ０ １ １ ０ |
０ １ １ ０ １ ０ １ １ |
１ ０ ０ １ ０ １ ０ ０ |
１ １ １ ０ １ ０ １ １ |
０ ０ ０ １ ０ １ ０ ０ |
１８ １２ １４ ６ １２ ８ １０ １６ |
１．予測式を求める
1.1 正規方程式を得て、予測式を求める。
各カテゴリについて行列式を作成し、Dとする。
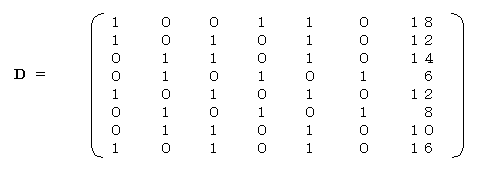
D'を求める。
＝TRANSPOSE(範囲）により、Dの転置行列D'を求める。
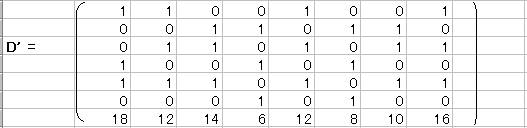
D'Dを求める。
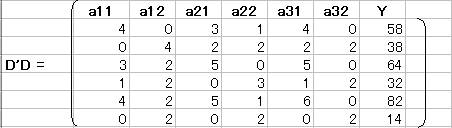
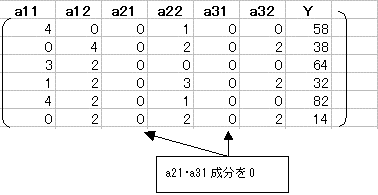成分a21・a31を０にする。
以上から下のような正規方程式を得る。
4a11 + a22
= 58
4a12 + 2a22 + 2a32 =38
3a11 +2a12 =64
a11 + 2a12 + 3a22 + 2a32 =32
4a11 + 2a12 + a22 =82
2a12 + 2a22 + 2a32 = 14
これを解くと、
a11 = 13.33 a12 = 12 a21 = 0 a22 = 4.667 a31 = 0 a32 = −9.667
1.2 成分a21･a31を取り除いた行列を使用して予測式を得る。
成分a21･a31を取り除いた行列をDとすると
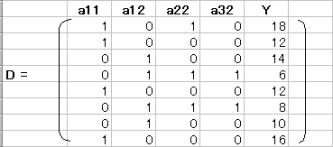
その転置行列D'は、＝TRANSPOSE(範囲）により、Dの転置行列D'を求める。
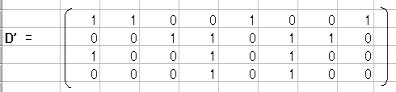
D'Dを求める
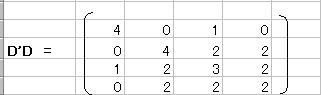
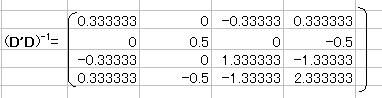
（D'D)-1を求める
（D'D)-1･D'を求める
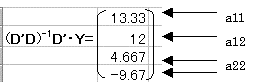D'D)-1･D'･Yを求める
以上から
a11 = 13.33 a12 = 12 a21 = 0 a22 = 4.667 a31 = 0 a32 = −9.667
予測式は、Y = 13.33X11 + 12X12 + 4.667X22 − 9.667X32
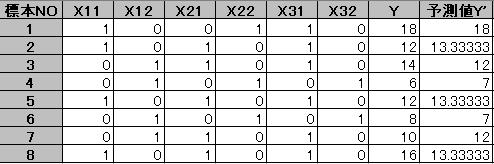
1.3 予測式 Y = 13.33X11 + 12X12 + 4.667X22 − 9.667X32で予測値を求める。
1.4 カテゴリ数量の基準化を行う。
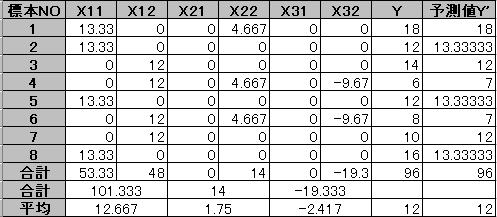
第1アイテム内のカテゴリ平均：12.667 第2アイテム内のカテゴリ平均：1.75
第３アイテム内のカテゴリ平均：−2.417 外的基準の平均：12
以上から
基準化した予測式Y'は
Y'−12＝(13.33−12.667)X11+(12−12.667)X12+(0−1.75)X21+(4.667−1.75)X22+(0−(−2.417))X31+(− 9.667−(−2.417))X32
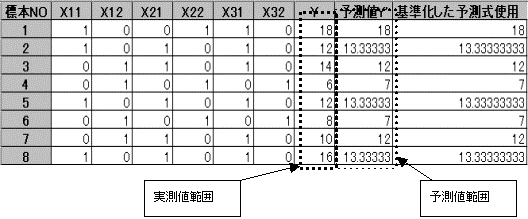
Y '= 0.667X11−0.667X12−1.75X21＋2.917X22＋2.41X31−7.25X32＋12
この基準化した予測式を使用して予測値を求めても同じ予測値を得ることができる。
２．重相関係数と偏相関係数を求める。
2.1 実測値と予測値から重相関係数求める。
重相関係数は、実測値と予測値の相関係数であるから、＝CORREL(範囲1，範囲2)から重相関係数を求める。
R＝CORREL(実測値範囲、予測値範囲）＝0.903037
2.2 基準化されたカテゴリデータから重相関係数を求める。
aij･Xijで各カテゴリを求める。
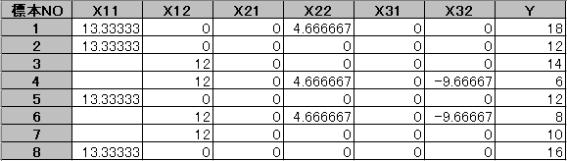
上のデータにおいて、それぞれのアイテムの各カテゴリを合計する。
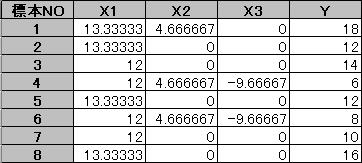
この新しい表を用いて、関数を使用し、各アイテム間の単相関係数を求める。
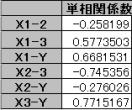
単相関係数行列をRとする
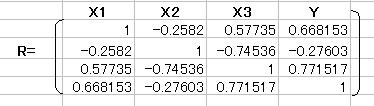
単相関係数Rの逆行列R-1を求める。
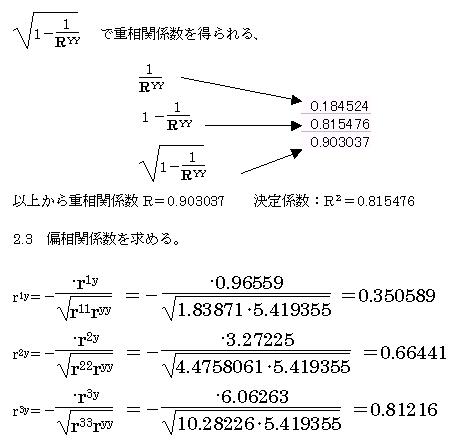
以上から求められた線形予測式により、実測値の約81.5%が説明されており、アイテム3の偏相関係数が一番大きいので、アイテム3がもっとも重要な要因であるといえる。
2.4 各アイテムの範囲（レンジ）を調べる。
各アイテムのレンジは基準化されたカテゴリデータの最大値−最小値で求められる。
アイテム1：13.333−12＝1.333
アイテム２：4.667−０＝4.667
アイテム３：0−(−9.667)＝9.667
アイテム３のレンジが一番大きい、よってアイテム３が外的基準に与える影響がもっとも大きいので、アイテム３が一番重要な要因である。