�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�z�[���ɖ߂�
�U�D�@EXCEL�ɂ��听�����͗��
�@�V���P�O���ɂ��āA�L���̓��e���j���[�X�E�r�W�l�X�E�X�|�[�c�ɂ��Ă��̏[���x���P�O�_�]���Œ��������B���̌��ʂ����̕\�ł���B
|
�m�n |
�j���[�X |
�r�W�l�X |
�X�|�[�c |
|
�w1 |
�w2 |
�w3 |
|
|
�P �Q �R �S �T �U �V �W �X �P�O |
�W �Q �W �R �V �S �R �U �T �U |
�X �T �T �T �S �R �U �W �S �V |
�S �V �U �S �X �S �W �Q �T �U |
��Ϗ[�����Ă���c�P�O�@�@�[�����Ă��Ȃ��c�O
�ȏ�̂P�O���ɂ��āA���̎��ʂ̏[���x��]�����邽�߂Ɏ听�����͂����{����B
���͂ɐ旧���ď�̃f�[�^����͂��Ă����B
�U�D�P�@���W���s���p���ĕ��͂����{����B
6.1 �听�������߂�B
6.1.1�@�ŗL�l�E�听�����חʂ����߂�
���W���s������߂�
2�ϗʊԂ̑��W�������߂���́A��CORREL(�͈�1�A�͈�2)�ł���B
���̊����g�p���ĕϗ�X1�|X2�AX1�|X3�AX2�|X3�Ԃ̑��W�������߂�B
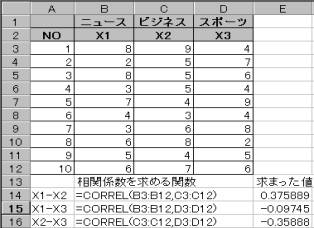
���W���s��́A
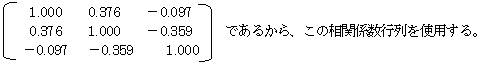
�ŗL�l�F�Ɂ@�ŗL�l�ɂɑ�����ŗL�x�N�g���F��1�E��2�E��3 �Ƃ���B

������A�R�̌ŗL�l�@��1=1.571
��2=0.903 ��3=0.527 �����߂���B
�A�ŗL�x�N�g�������߂�
�@�@�ŗL�l ��1=1.571�̎�
�@�@
�@�@
������ŗL�x�N�g���́@��1��0.531�@��2��0.673�@��3���|0.514
�@�@
�@�@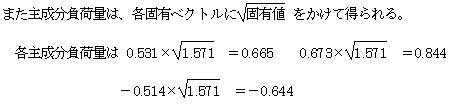
�@�@�ŗL�l�@��2��0.903 �̂Ƃ�
�@�@ �ŗL�x�N�g���́@��1��0.689 ��2��0.0095
��3��0.724�@�@�@�@
�听�����חʂ́@ 0.655 0.009 0.688
�ŗL�l�@��3��0.527 �̂Ƃ�
�@�@ �ŗL�x�N�g���́@��1���|0.492 ��2��0.738
��3��0.459 �@�@�@�@
�听�����חʂ́@ �|0.357 �@
0.536 0.333
�ȏ���܂Ƃ߂��
|
�ŗL�l |
��P�听�� 1.571 |
��Q�听�� 0.903 |
��R�听�� 0.527 |
|
�ŗL�x�N�g�� |
0.531 0.673 -0.514 |
0.689 0.0095 0.724 |
�|0.492 0.738 0.459 |
|
�听�����ח� |
0.665 0.844 -0.644 |
0.655 0.009 0.688 |
�|0.357 0.536 0.333 |
�U�D�Q�@�ׂ���@����ŗL�l�E�ŗL�x�N�g�������߂�B
�@���W���s��A����������悤�ȌŗL�l�Ȃ�тɌŗL�x�N�g�������߂邱�Ƃ́A��ςł���B�����ŁA�ׂ���@��p���ČŗL�l�ƌŗL�x�N�g�������߂�B
�@�@
�@�@
�ׂ���@�Ƃ́A���W���s����`�Ƃ���Ƃ��A���������ׂĂP���w�s����l����B
�@�@
���̋��߂�ꂽ�s��ōő�̐�����1�ɕϊ�����
�@�@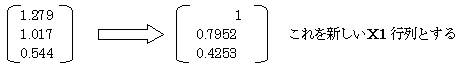
�����āA�`��w1���v�Z����B
�@�@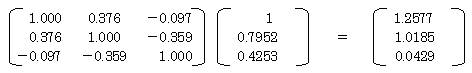 �@
�@
���̋��߂�ꂽ�s��ōő�̐�����1�ɕϊ�����
�@�@
�����āA���l�ɂ����`��w2���v�Z����B
���̍�Ƃ��J��Ԃ����{���A���߂�ꂽ�s��̐����ŁA�ő�̒l�̂��̂�1�O�ɔ��10-5���x�܂ł̍��ƂȂ�����A�I������B���̎��ő�̐�����1�Ԗڂ̌ŗL�l�ƂȂ�A�܂����̎��̂w������W��������ƁA1�Ԗڂ̌ŗL�l�ɑ�����ŗL�x�N�g�������߂���B
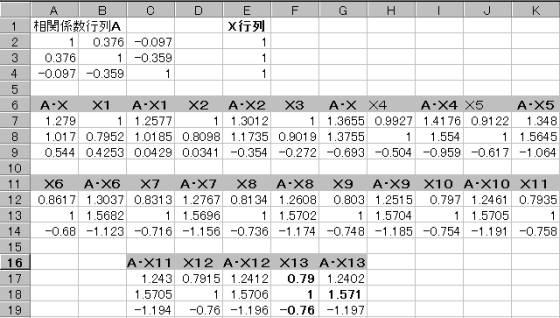
���߂�ꂽ�s��ōő�̐����̒l�́A��̕\�ł͕�����Ȃ����A���{�v�Z���Ă����ƁA1.57056�|1.157055��0.00001�@�ƂȂ�AA�X13�Ŏ����������ł���B
���̎��̍ő�̐�����1.57056�ł���A���ꂪ1�Ԗڂ̌ŗL�l�ł���B
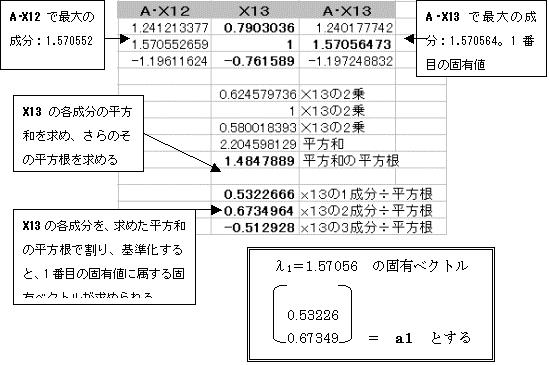
2�Ԗڈȍ~�̌ŗL�l�����߂�ɂ́AA1��A�|���Pa1a1�f
�Ƃ��čēx�ŏ�����ׂ���@���J��Ԃ��B
A1��A�|���Pa1a1�f�ɂ��V����A1�����߂�B
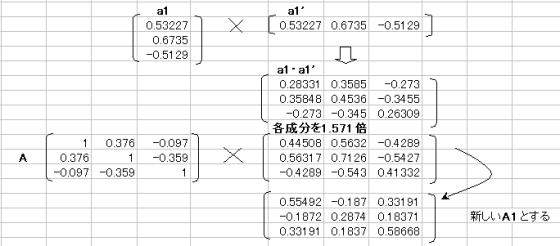
���̐V����A1���g�p���čēx�ׂ���@�����{��2�Ԗڂ̌ŗL�l�E�ŗL�x�N�g�������߂�B
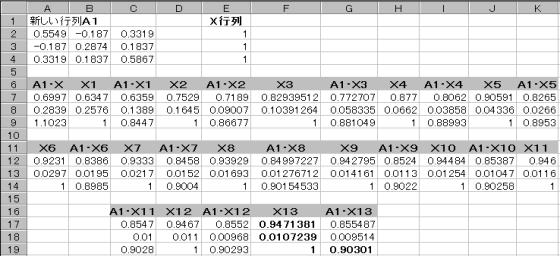

3�Ԗڂ̌ŗL�l�E�ŗL�x�N�g�������l�ɂ��ċ��߂�B
�U�D�R�@�听�����חʂ̃v���b�g������B
�����ɑ�P�听���A�c���ɑ�Q�听�����Ƃ�A�听�����חʂ��O���t�ɕ`���Ă݂�B
�@�@�@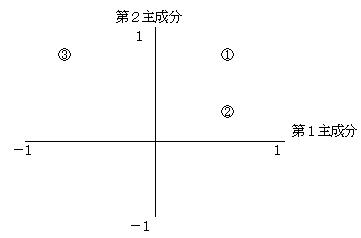
�@�听�����חʂ́A�听���Ɗe�ϗʂ̊Ԃ̑��W���Ɉ�v���A�听�����חʂ��P�ɋ߂��قǂ��̕ϗʂƎ听���̊W���[�����Ƃ������Ă���̂ŁA�e�ϗʂ̎听�����חʂ��݂Ă����B
�@��P�听���̎听�����חʂ́A�j���[�X�F0.665
�r�W�l�X�F0.844 �Ɠ����x�ɑ傫���A�X�|�[�c�͕��i�|�j�ƂȂ��Ă���B���̂��Ƃ���A��P�听���̓j���[�X�ƃr�W�l�X�W�𒆐S�Ɏ听�����חʂ��傫���A�X�|�[�c�W�̕��חʂ͒Ⴂ�̂ŁA��历�u���x���v��ړx�ƍl����厏�u���x�Ɩ��t����B��Q�听���̎听�����חʂ́A�j���[�X�F0.655 �X�|�[�c�F0.688 �Ɠ����x�ɑ傫�����A�r�W�l�X�F0.009 �ƂȂ��Ă���B���̂��Ƃ����Q�听���͑�O���u���x���v��ړx�ƍl����O���u���x�Ɩ��t����B
�@�܂��A��P�听���E��Q�听���E��R�听���̂��ꂼ��̌ŗL�l�E�ݐϊ�^���i���j���݂�ƁA
�ŗL�l���P�ȏ�܂��͗ݐϊ�^�����U�O���ȏ�̂��̂��̗p����Ƃ���ƁA��Q�听���܂ō̗p����悤�ɂ���B
�U�D�S�@�听�����_�����߂�B
6.4.1�@��1�听�����_�����߂�B
![]()
���̎���p���āA��P�听�����_�����߂�B

X1�`X3�̐����ϗʂɕW���������l��p���Ď听�����_�����߂�B���̎��听�����_�̗L�l����v���Ă��邱�Ƃ�������B���߂��听�����_������ɕW���������l�����߂�B
6.4.2�@��2�听�����_�����߂�B
![]()
���̎���p���āA��Q�听�����_�����߂�B
|
NO |
�听�����_ |
�W���� |
|
1 2 3 4 5 6 7 8 9 10 |
0.424 �|0.545 1.123 �|1.286 1.859 �|0.959 0.158 1.957 �|0.256 0.458 |
0.447 �|0.573 1.182 �|1.354 �|0.976 �|1.010 0.167 �|1.028 �|0.269 0.482 |
|
���� |
0.000 |
0.000 |
|
���U |
0.903 |
1.000 |
|
STD |
0.950 |
1.000 |
��R�听���ɂ��Ă��A��R�听���̌ŗL�x�N�g����p���āA���l�Ɍv�Z���ċ��߂�B
��P�听�����_�E��Q�听�����_�E��R�听�����_�̂��ꂼ�ꂨ�݂��̑��W�������߂�ƁA��������O�ƂȂ薳���ւł��邱�Ƃ��킩��B���݂��ɓƗ��ł��邱�Ƃ��킩��B
�@
��P�听���̌ŗL�l�F1.571 ��Q�听���̌ŗL�l�F0.903 ��R�听���̌ŗL�l�F0.527�@ ����́A��P�听�����_�̕��U�A��Q�听�����_�̕��U�A��R�听�����_�̕��U�Ɉ�v���Ă��邱�Ƃ��킩��B���U�̑傫���f�[�^�Q�قǐ����͂��傫���̂ł��d�v�ȃf�[�^�ł���B�ŗL�l�̑傫���قǏd�v�ȃf�[�^�ł���Ƃ�����B
�@��P�听�����_����A��厏�u���x����ԍ����̂͂m�n�P���ł��莟�ɂm�n�W���ł���A��ԏ������̂͂m�n�Q���ł��邱�Ƃ��킩��B���ɑ�Q�听�����_�����O���u���x����ԑ傫���̂͂m�n�T���ł���A��ԏ������̂͂m�n�S���ł��邱�Ƃ��킩��B
�U�D�T�@���U�E�����U�s���p������@
6.5.1 �听�������߂�B
�i�P�j���U������U�����߂�
�@���U�����߂���́A��VARPA(�͈�)�ł���B�܂������U�����߂���́A��COVAR(�͈�1�A�͈�2)�ł���B����2�̊����g�p���ĕ��U�E�����U�����߂�B
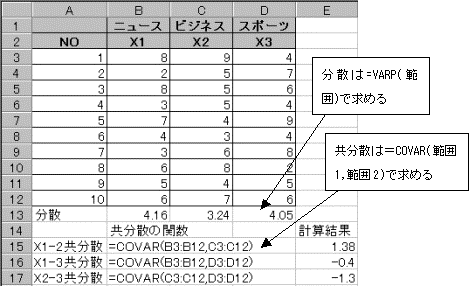
�i�Q�j�ŗL�l�E�听�����חʂ����߂�
���U�E�����U�s���
�@�@�@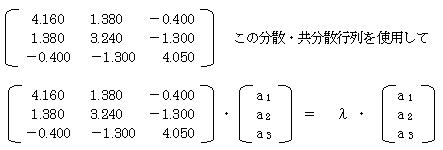
������A�R�̌ŗL�l�@��1=5.8731
��2=3.7023 ��3=1.8746 �����߂���B
�i�R�j�ŗL�x�N�g�������߂�
�@�@�ŗL�l ��1 = 5.8731�̎�
�@�@�@
������ŗL�x�N�g���́@��1��0.598�@��2��0.582�@��3���|0.548
�ȉ����l�ɂ���
�@�@�ŗL�l��2��3.7023�̂Ƃ��̌ŗL�x�N�g���@��1�� 0.683 ��2���|0.0148 ��3��0.7305
�ŗL�l��3��1.8746�̂Ƃ��̌ŗL�x�N�g���@��1���|0.419 ��2�� 0.812
��3��0.408
�ȏ���܂Ƃ߂��
|
�ŗL�l |
��P�听�� 5.8731 |
��Q�听�� 3.7023 |
��R�听�� 1.8746 |
|
�ŗL�x�N�g�� |
0.5986 0.5843 �|0.548 |
0.683 �|0.0148
0.7303 |
�|0.4185 0.8114 0.4079 |
6.5.2�@�听�����_�����߂�B
�i�P�j ��P�听�����_�����߂鎮�́A
�@�@�@�@![]()
���̎���p���āA��P�听�����_�����߂�B
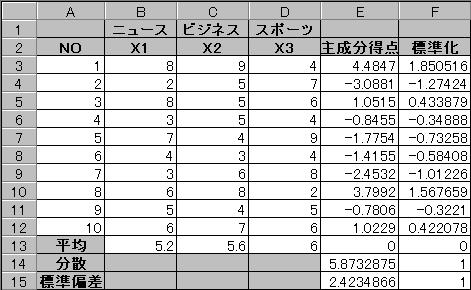
���߂�ꂽ�听�����_������ɕW�������A���ρF�O�@���U�F�P�@�Ƃ���B
�i�Q�j��Q�听�����_�����߂�B
�@�@�@![]()
���̎���p���āA��Q�听�����_������B
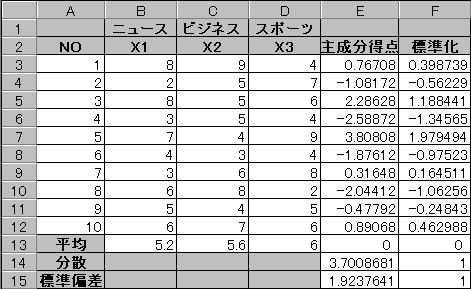
��R�听�������߂鎮��
�@�@�@![]()
���̎���p���āA��R�听�����_�����߂�B
�@��P�听�����_����A��历�u���x����ԍ����̂͂m�n�P���Ŏ��ɂm�n�W���ł���A��ԏ������̂͂m�n�Q���ł��邱�Ƃ��킩��B���ɑ�Q�听�����_�����O���u���x����ԑ傫���̂́A�m�n�T���ł���A��ԏ������̂͂m�n�S���ł��邱�Ƃ��킩��B
�@�听�����_�����߂�̂ɁA���W���s��o�������߂���@�ƁA���U�����U�s��o�����ċ��߂���@�ƂQ�ʂ���s�������A���W���s��o�����ċ��߂��听�����_�ƕ��U�����U�s��o�����ċ��߂��听�����_�̏��ʂ͕K��������v���Ȃ��B����̗�ł́A�R�ϗʂ̒P�ʂ������ł���̂ŁA�ʏ핪�U�����U�s��听�����_�����߂�B