�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�z�[���ɖ߂�
�T�D�@�听������
�@�听�����͂́A���֊W�ɂ��邢�����̗v���������i���k�j���āA�������̐����ɂ��A���̑����͂���������߂���@�ł���B�听�����͂ł́A�d��A���͂┻�ʕ��͂̂悤�ɖړI�ϗʂ͗^�����Ă��Ȃ��B�����ϗʂ����k���Ă��̓����ׂ���̂ł���B
�@�Ⴆ�A���l���̐��k�̉p��E���w�E���ȁE�Љ�̂S�̐��уf�[�^����A���̂S�̗v�������k���P�����̃f�[�^�ɂ��邱�Ƃɂ��A���̐��k�̑����ׂ͂���A�܂����n�\�́E���n�\�ׂ͂�Ȃǂ̂悤�ɂ�����������߂��肷����@�ł���B
�T�D�P�@�听�������߂�
�@�W�l�̐��k�̉p��Ɛ��w�̕]�������\�̂悤�ł������Ƃ���B���̌X�̐��т��瑍���͂͒N����Ԃ���̂��A�܂����n�\�́E���n�\�͂̂ǂ��炪����̂��ׂ�B
|
No |
�W�{ |
�p�� ��1 |
���w ��2 |
���v |
���� |
|
�P �Q �R �S �T �U �V �W |
�` �a �b �c �d �e �f �g |
�T �T �V �W �V �S �W �S |
�W �T �S �T �Q �R �V �U |
�P�R �P�O �P�P �P�R �X �V �P�T �P�O |
�Q �T �S �Q �V �W �P �T |
|
|
���@�� |
�U |
�T |
|
|
�P���ɉp��Ɛ��w�̍��v���珇�ʂ�����ƁA��̕\�̂悤�ɂȂ�B���������̏��ʂ������͂������Ă��邩�ǂ����͕s���ł���B�����ʼnp��i��1�j�Ɛ��w�i��2�j�̃f�[�^�����k���ĂP�����ɍ������A�ړx���P�ɂ��Ă��瑍���͂����߂邱�Ƃ��l����B
�Q�����ł��邾�����̏�������Ȃ��悤�ɂ��āA�P�̏��ɍ������Ă��炻�̑����ׂ͂Ă݂�B�Q�ϗʂ������������̂��y�Ƃ���ƁA�Q�ϗʂ���������̂ŁA�K���ȏd�݂�i�����āA�y����1�x1�{��2�x2�@�Ƃ���B
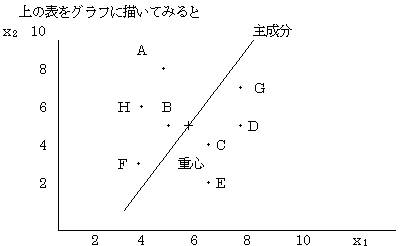
�ʏ�A�听�������߂�ɂ́A�W�{�f�[�^�̏d�S��ʂ钼�����P�{�����B���̒����͓K���ȏd�݁@��i����
�y����1�x1�{��2�x2�{�c�{��n�xn �Ȃ钼�����l����B�����Ă��̒����́A�e�_����̒����ւ̋������ŏ��ɂȂ�悤�Ɉ����K�v������B���̂悤�ɂ���ɂ́A��12�{��22�{�c�{��n2���P�̏������ō����ϐ��y�̕��U���ő�ɂȂ�悤�ɂ���B�܂��A�����鍇���ϐ��y�̂������U���ő�̂��̂��P�听���A���̎��ɕ��U���傫����P�听���Ƃ͖����ւ̂��̂��Q�听���Ƃ����B��ʂɂ͕ϗʂ�������A���̎听���܂ŋ��߂邱�Ƃ��ł���B
�@�O�̗�ɂ����āA�d�S��ʂ钼�����y����1�x1�{��2�x2�Ƃ���B���̒����́A�e�W�{�f�[�^����̂��̒�����ւ̋������ŏ��ɂȂ�悤�Ɉ����B
�@���܁A�}�̂P�_�c���炱�̒����y��ɍ~�낵���_���p�Ƃ����
�@�@�@�@�@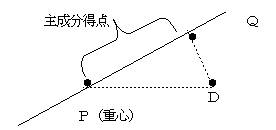
�o�c2���o�p2�{�c�p2 �ł���A�o�c2 �͎��ۂ̏��ʂł��邩����ł���B���ܓ_�c���炱�̒�����ւ̋������ŏ��ɂ���i�������邱�Ƃɂ�莸������ʂ��ŏ��ɂ���j���Ƃ��l����̂łc�p2���ł��邾���������������A����Ƃo�p2 ���ő�ɂ���i�������ċ��߂���ʂ��ő�ɂ���j���Ƃ��l����悢�B
�@�Ȃ��A�d�S�o����_�p�܂ł̋������听�����_�Ƃ����B���̎听�����_���Q�ϗʂ����������l�ł���B���听�����y1����1�x1�{��2�x2 �Ƃ���ƁA�听�����_�̕��U�p��
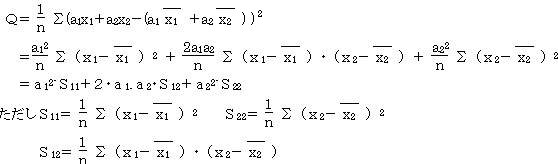
��12�{��22���P�̏������ŁA���̎听�����_�̕��U�p���ő�ɂ���悤�Ȃ�1���2�����߂�B
�@ ���O�����W���̖���搔�@��p����
�@�@�f���p�|�Ɂi��12�{��22�|�P�j�Ƃ����āA�f����1���2�ŕΔ������O�Ƃ������Ƃɂ�蕪�U�p���ő�ɂ��邁1���2 �����߂�B
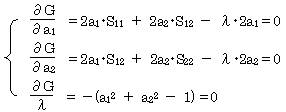
![]() �i�r11�|�Ɂj���1�{�r12���2���O
�i�r11�|�Ɂj���1�{�r12���2���O
�r12���1�{�i�r22�|�Ɂj���2���O
��12�{��22���P
������s����g�p���ĕ\���ƁA���̂悤�ȌŗL�������ƂȂ�B
�@�@�@
��P�听���Ƃ��ẮA�傫�����̃ɒl���̗p����B
5.1.1�@���U�����U�s��听�������߂�B
�听�����_�̕��U�p���ő�ɂ��邁1���2�����߂�ɂ́A���U�����U�s����g�p���čs�����Ƃ��ł���B
�i�P�j�����ϗʂQ�̎��A���U�����U�s��o�����Ď听�������߂�B
�@�@�@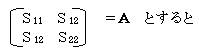
�`�w�����w �i�ɁF�����j
�������A�ɂ��`�̌ŗL�l�A�w���ɂɑ�����ŗL�x�N�g���Ƃ����B�ŗL�l�ɂ͎听�����_�̕��U�Ɉ�v����B
�@�@�@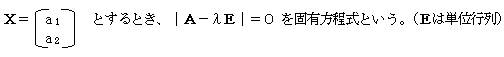
���̌ŗL����������ŗL�l�ɂ����߂�B
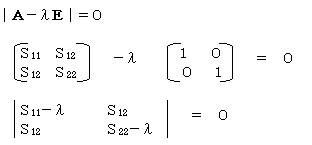
�i�r11�|�Ɂj��i�r22�|�Ɂj�|�r122���O �ƂȂ�A��قnjv�Z�������ʂƓ������̂邱�Ƃ��ł���B
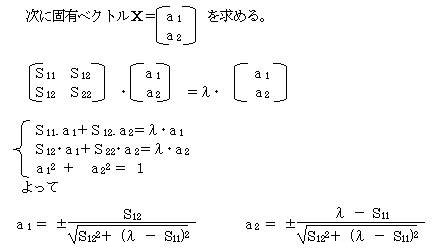
��P�听���̎��͂y1����1���1�{��2���2�@�ł��邪�A���_���O����f�[�^�̏d�S�i��1�C��2�j�Ɉړ�����ƁA![]() �ƂȂ�B���̎���p���Ď听�����_�����߂邱�Ƃ��ł���B
�ƂȂ�B���̎���p���Ď听�����_�����߂邱�Ƃ��ł���B
�i�Q�j�����ϗʂ������鎞�A���U�����U�s��o�����Ď听�������߂�B
�����ϗʂ������鎞�̕��U�����U�s����`�Ƃ����
�@�@�@�@�@
���̎� �`�w�����w
�i�ɁF�����j �̌ŗL�������������ČŗL�l�ɂ�B�ŗL�l�ɂ���1����2���c����p���O�Ƃ���ƁA�ŗL�l�̑傫�����@���珇�ɁA��P�听���E��Q�听���c�悐�听���ƂȂ�̂ŁA�e�ɂɑ�����ŗL�x�N�g�������߂�ƁA�e�听���̌W���邱�Ƃ��ł���B
�@�@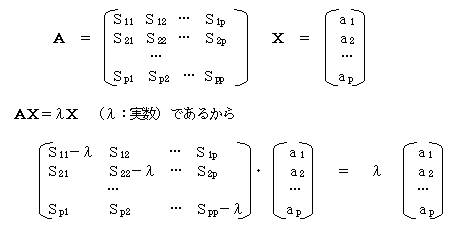
����ŗL�l��i��B
�ő�̌ŗL�l��1����A��P�听����������̂ŁA��1�ɑ�����ŗL�x�N�g����i�����߂đ�P�听���̎������߂���B
��P�听�̎��c �y1����1���1�{��2���2�{�c��p���p�{��0
���l�ɂ��āA�Q�Ԗڂɑ傫���ŗL�l��2�����Q�听���̎��邱�Ƃ��ł���B��2�ɑ�����ŗL�x�N�g����j�����߂đ�Q�听���̎������߂���B
��Q�听�̎��c �y2����1���1�{��2���2�{�c��p���p�{��0
�ȉ��A���l�ɂ��đ悐�听���܂ŋ��߂邱�Ƃ��ł���B
5.1.2�@���֍s��听�������߂�B
�@�����ϗʂ̒P�ʂ��قȂ�Ƃ��ɂ́A�P�ʂ̉e�����Ă��܂��听�������߂邱�Ƃ��ł��Ȃ��B���̂悤�ȂƂ��A�P�ʂ̉e������菜���ɂ́A�f�[�^�̕W����������悢�B
�f�[�^�̕W������
![]()
�ŕϊ������f�[�^�ɂ��Ď听�������߂�悢�B�f�[�^�̕W�������s���ƁA���ρ��O�@���U���P�ƂȂ�B���U�����U�s��̓f�[�^�̕W�������s���ƁA���֍s��ƂȂ�B
�i�P�j�ϗʂ��Q�̎��A���֍s��o�����Ď听�������߂�B
�ŗL��������
�b�`�|���d�b���O �i�P�|�Ɂj2 �|��122 ���O�@�Ɂ��P�}��12

�i�Q�j�ϗʂ��Q�̎��A���֍s��o�����Ď听�������߂�B
�����ϗʂ������鎞�̑��֍s����`�Ƃ����
���U�����U�s��o�������Ƃ��Ɠ��l��
�`�w�����w�@�i�ɁF�����j�̌ŗL�������������ČŗL�l�ɂ�B�ŗL�l�ɂ���1����2���c����p���O�Ƃ���ƁA�ŗL�l�̑傫�����@���珇�ɁA��P�听���E��Q�听���c�悐�听���������A�e�ɂɑ�����ŗL�x�N�g�������߂āA�e�听���̌W����B
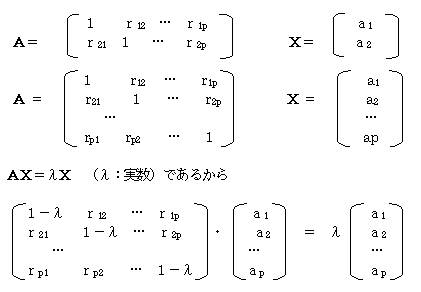
����ŗL�l��i��B
�ő�̌ŗL�l��1����A��P�听����������̂ŁA��1�ɑ�����ŗL�x�N�g����i�����߂đ�P�听���̎������߂���B
��P�听�̎��c �y1����1���1'�{��2���2'�{�c��p���p'�{��0
�������A��i'�͕W���������l�ł���B
���l�ɂ��āA�Q�Ԗڂɑ傫���ŗL�l��2�����Q�听���̎��邱�Ƃ��ł���B��2�ɑ�����ŗL�x�N�g����j�����߂đ�Q�听���̎������߂���B
��Q�听�̎��c �y2����1���1'�{��2���2'�{�c��p���p'�{��0
�ȉ��A���l�ɂ��đ悐�听���܂ŋ��߂邱�Ƃ��ł���B
�Ȃ��V�������߂�ꂽ�听���́A�����ϗʂ��������ē�������̂ł��邩��A�V���Ɏ����ł��̎听���������Ӗ�����ϗʂł��邩��������K�v������B
�T�D�Q�@���ɂ���
5.2.1�@�听�������߂�
|
No |
�W�{ |
�p��i��1�j |
���w�i��2�j |
|
�P �Q �R �S �T �U �V �W |
�` �a �b �c �d �e �f �g |
�T �T �V �W �V �S �W �S |
�W �T �S �T �Q �R �V �U |
|
|
���@�� |
�U |
�T |


(2.5�|��)�(3.5�|��) �| 0.1252=0
��=3.515 , 2.484
�听�����_�̕��U��傫������̂Ń� = 3.515���P�听���Ƃ��č̗p����B
��P�听��
��1 = 3.515 �̎��̌ŗL�x�N�g�������߂��
�@�@�@�@�@�@��1 = �|0.122 ��2 =
0.9925
����� Z1 ���|0.1222�(x1�|6)�{0.9925�(x2�| 5) =�|0.1222�x1�{0.9925�x2�|4.229
��Q�听��
��2 = 2.484 ����
�@�@�@�@Z2 �� 0.9925�x1 �{ 0.1222�x2 �| 6.566 �ƂȂ�B
5.2.2�@�听�����_�����߂�
��P�听�����_�́AZ1���|0.1222�x1�{0.9925�x2�|4.229 ���狁�߂�Ɖ��\�̂悤�ɂȂ�B
|
No |
�W�{ |
�p�� ��1 |
���w ��2 |
��P�听�����_ |
���� |
|
�P �Q �R �S �T �U �V �W |
�` �a �b �c �d �e �f �g |
�T �T �V �W �V �S �W �S |
�W �T �S �T �Q �R �V �U |
3.0997 0.1222 �|1.1147 �|0.2444 �|3.0997 �|1.7406 1.7406 1.2369 |
�P �S �U �T �W �V �Q �R |
|
���� |
|
�U |
�T |
|
|
|
���U |
|
|
|
|
3.515 |
��P�听���̎�������Ƃ�1�i�p��j�̌W�����i�|�j�ł�2�i���w�j�̌W�����i�{�j�ƂȂ��Ă���B���ꂩ��A��P�听���͗��n�\�͂������ƍl������B�听�����_���炻�̓_���̑傫�����ɏ��ʂ�����ƁA���̏��ʂ����n�\�͂̏��ʂł���Ƃ�����B
������O���t�ɕ`���Ă݂��
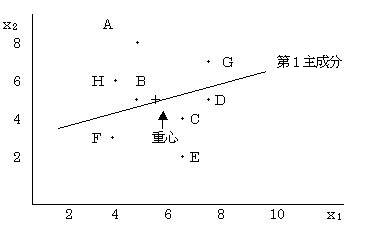 �@
�@
��Q�听�����_�́AZ1��0.9925�x1�{0.1222�x2�|6.566 ���狁�߂�Ɖ��\�̂悤�ɂȂ�B
|
No |
�W�{ |
�p�� ��1 |
���w ��2 |
��Q�听�����_ |
���� |
|
�P �Q �R �S �T �U �V �W |
�` �a �b �c �d �e �f �g |
�T �T �V �W �V �S �W �S |
�W �T �S �T �Q �R �V �U |
�|0.6259 �|0.9925 0.8703 1.985 0.6259 �|2.2294 2.2294 �|1.8628 |
�T �U �R �Q �S �W �P�V |
|
���� |
|
�U |
�T |
2.484 |
|
|
���U |
|
|
|
|
|
��Q�听���̎�������Ƃ�1�i�p��j�̌W���Ƃ�2�i���w�j�̌W�����Ƃ��Ɂi�{�j�ƂȂ��Ă���B���ꂩ��A��Q�听���͑����͂������ƍl������B�听�����_���炻�̓_���̑傫�����ɏ��ʂ�����ƁA���̏��ʂ������͂̏��ʂł���Ƃ�����B
������O���t�ɕ`����
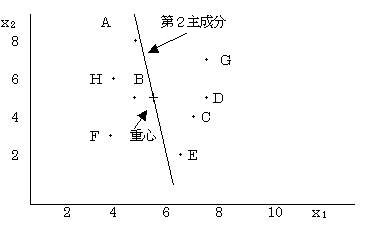
��P�听�����_�̕��U��3.515�@��Q�听�����_�̕��U��2.484�ł���B���̒l�͌ŗL�l�Ɉ�v���Ă��邱�Ƃ�������B�܂���P�听���Ƒ�Q�听���Ƃ͖����ւł��邩��A���݂��̒����͒����s����B�W�����u�|�����킹��ƂO�ƂȂ�B
�@�@�@(�|0.1222)�~0.9925�{0.1222�~0.9925 = 0
�T�D�R�@��^��
���̕ϗʂ�����ƁA�听���������߂邱�Ƃ��ł���B�������A�听�����͂́A���̕ϗʃf�[�^�����k���ĕ��͂�����@�ł��邩��A�听���������߂�K�v�͂Ȃ��B
�����ŁA��P�听�����珇�ɑ�Q�听���c�悐�o�����Ƃ��ꂼ��̎听�������Ƃ̃f�[�^���ǂ�ʐ������Ă���̂��������ړx�Ƃ��āA��^��������B
�ŗL�l�̑傫���قǁA�听�����_�̕��U���傫���A���Ƃ̃f�[�^���������͂��傫���i���ʂ������j�̂ŏd�v�ł���Ƃ�����B
���܁A���̂悤�ɑ悐�听���܂ł���A���̌ŗL�l�����ꂼ���i�Ƃ����
��^���́A���ꂼ��̌ŗL�l���ŗL�l�̍��v�Ŋ��������̂ł���B
|
�听�� |
�ŗL�l |
��^�� |
|
��P�听�� ��Q�听�� �c �悐�听�� |
��1 ��2 �c ��p |
��1�^��T ��2�^��T �c ��p�^��T |
|
���@�v |
����i����T |
|
��^�����P�听�����珇�ɗݐς��Ă��������̂��A�ݐϊ�^���ƌĂԂ��A��ʂɗݐϊ�^�����U�O���ȏ�ɂȂ�܂ł̎听�����̗p����B�܂����֍s��听�������߂�Ƃ��@�@�@�ɂ́A�ŗL�l���P�ȏ�̂��̂��̗p����B
���֍s��听�������߂��Ƃ��̊�^����
�@�@�@![]()
�T�D�S�@�听�����ח�
�@���Ƃ̃f�[�^�Ǝ听���ŋ��߂��f�[�^�Ԃɂǂꂭ�炢�W�����邩���邽�߂̂��̂Ƃ��āA�听�����חʂ�����B�听�����חʂ́A�\���W���Ƃ��Ă�Ă���B
�@�听�����חʁ����Ƃ̃f�[�^�Ǝ听�����_�Ƃ̑��W��
�听�����חʂƌŗL�l�Ƃ̊W
�@���U�����U�s��听�������߂���

�T�D�T�@�̗p����听���̐��ɂ���
�@��ʂɁA�����ϗʂ�������Ύ听�����悐�听���܂ŋ��߂邱�Ƃ��ł���B�������听�����̖͂ڕW���̂������ϗʂ̈��k�ł���A�悐�听���܂Ŏg�p�Ȃ��Ă��\���ɂ��Ƃ̏�������ł���ꍇ�����Ȃ��Ȃ��B����ł́A�听���������܂Ŏ��グ��悢���Ƃ������ƂɂȂ�B�听���́A��P�听������ԕ��U���傫�����ʂ������Ƃ�����B���ɑ�Q�听���Ƃ����悤�ɏ��X�ɏ��ʂ��������Ȃ�̂ŁA��P�听������悎�听���܂ł̊�̎听�������グ����悢������������B
5.5.1 ��܂ł̎听�������グ����悢���̖ڈ�
(1)�ݐϊ�^�����U�O���ȏ�̂��̂܂Ŏ听�������グ��B
�ݐϊ�^���������ȏ�ɂȂ�܂Ŏ��グ��ׂ����ɂ��ẮA���Ɋ�͂Ȃ����A�Œ�ł��U�O���ȏ�ɂȂ�܂ł̎听�������グ���ق����悢�B
(2)���֍s��o�������Ƃ��ɂ́A�ŗL�l���P�ȏ�̂��̂����グ��B