ホームに戻る

８．　正準相関分析例題

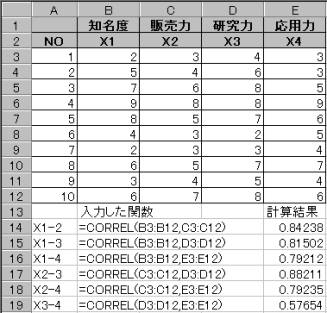
　１０社についてその知名度・販売力・研究力・応用力について１０点満点で評価をし、下のような表を得たとする。

 

標本NO	知名度 Ｘ1	販売力 Ｘ2	研究力 Ｘ3	応用力 Ｘ4
１ ２ ３ ４ ５ ６ ７ ８ ９ １０	２ ５ ７ ９ ８ ４ ２ ６ ３ ６	３ ４ ６ ８ ５ ３ ３ ５ ４ ７	４ ６ ８ ８ ７ ２ ３ ７ ５ ８	３ ３ ５ ９ ６ ５ ４ ７ ４ ６

 

　いま上記のように４変量ある時、知名度（Ｘ₁）と販売力（Ｘ₂）を合成した営業力と、研究力（Ｘ₃）と応用力（Ｘ₄）を合成した技術力とがどの様な関係にあるか正準相関係数を求めて調べてみる。

知名度（Ｘ₁）と販売力（Ｘ₂）の正準変量をＺ、研究力（Ｘ₃）と応用力（Ｘ₄）の正準変量をＷとする。それぞれの正準変量をＺ＝ｌ₁･Ｘ₁＋ｌ₂･Ｘ₂　  Ｗ＝ｍ₁･Ｘ₃＋ｍ₂･Ｘ₄　とする。

８．１　重み係数を求める。

　相関係数行列を求める。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

	Ｘ1	Ｘ2	Ｘ3	Ｘ4
Ｘ1	1.000	0.842	0.815	0.792
Ｘ2	0.842	1.000	0.882	0.792
Ｘ3	0.815	0.882	1.000	0.577
Ｘ4	0.792	0.792	0.577	1.000

　　

     Ｒ₁₁^-1・Ｒ₁₂・Ｒ₂₂^-1・Ｒ₂₁ を求めると

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

　　

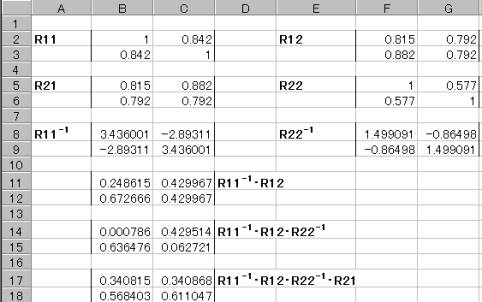
    また　ｌ’･Ｒ₁₁･ｌ ＝ １　であるから

　　

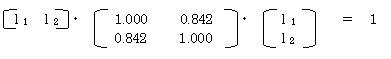
 以上から

           ｌ₁²＋1.684･ｌ₁･ｌ₂＋ｌ₂²＝１ 　　　　

           0.34081･ｌ₁＋0.34086･ｌ₂＝0.936･ｌ₁  

           0.56840･ｌ₁＋0.61104･ｌ₂＝0.936･ｌ₂  

 

 これより　ｌ₁＝  ±0.378  ｌ₂＝  1.746×（±0.378）＝±0.660

　ＺとＷは正の相関がありそうなので、正の値を採用して

　　　

 

 

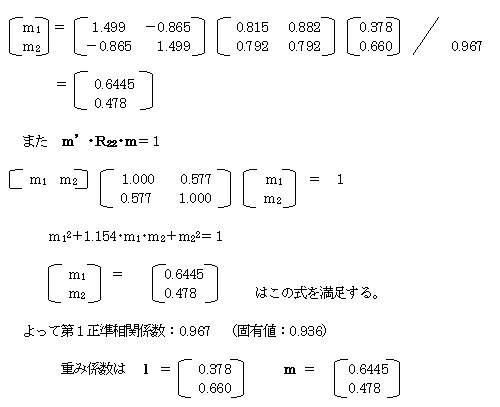
  第２正準相関係数についても、λ²＝0.124（固有値：0.0154）を使用して同様にして求める。

 

 

　　

                        

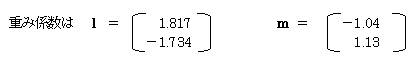
	第1成分	第２成分
固有値	0.936	0.0154
相関係数	0.967	0.124
重み係数	Ｘ1    Ｘ2    Ｘ3     Ｘ4 0.378  0.660  0.6445  0.478	Ｘ1    Ｘ2  Ｘ3   Ｘ4 1.817 −1.734 −1.04  1.13

 

８．２　正準変量を求める。

  　　実際に求めた第１正準変量の重み係数を用いて正準変量のＺ₁とＷ₁ 求める。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

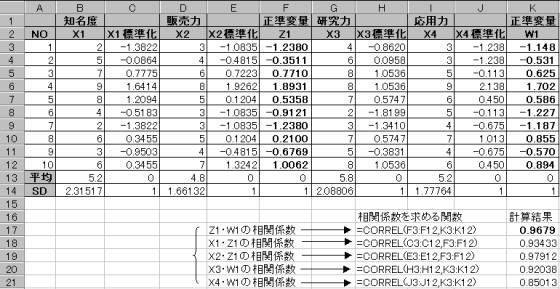
  標準化した値を使用して、第１正準変量のＺ₁とＷ₁を求めると上の表のようになる。

  このＺ₁とＷ₁の相関係数を求めると　Ｒ_ZW ＝0.9679　となり第１正準相関係数に一致。

 

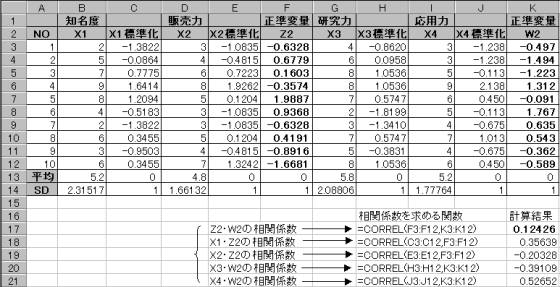  次に、第２正準変量の重み係数を用いて正準変量のＺ₂とＷ₂ 求める。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  第２正準変量のＺ₂とＷ₂を求めその相関係数を求めると0.124となり同様に第２正準相関係数に一致している。

  それぞれの正準変量間の相関係数を求めると、Ｚ₁とＺ₂　Ｚ₁とＷ₂　Ｗ₁とＺ₂　Ｗ₁とＷ₂のいずれにおいてもその相関係数は０となっている。

 

 

８．３　構造係数を求める。

　構造係数は、各変量と正準変量間の相関係数であるから、標準化した各変量と正準変量と　　　の相関係数を求める。

      標準化した変量Ｘ₁ と第１正準変量Ｚ₁の相関係数をＲ_X1−Z1 とすると

             　　　　　 　Ｒ_X1−Z1 ＝ 0.9343

      同様に求めていくと  Ｒ_X2−Z1＝ 0.9791   Ｒ_X3−W1＝ 0.204  Ｒ_X4−W1＝ 0.8501

      標準化した変量Ｘ₁ と第２正準変量Ｚ₂の相関係数をＲ_X1−Z2 とすると

                          Ｒ_X1−Z2 ＝ 0.3564

      同様に求めていくと  Ｒ_X2−Z2＝ −0.2033  Ｒ_X3−W2＝−0.3910 Ｒ_X4−W2＝ 0.5266

８．４　正準相関係数の検定を行う。

（１）母集団における第１正準相関係数の検定を行う

      母集団における第１正準相関係数をρ₁ とする。

　 (1)仮説をたてる

　　　帰無仮説：Ｈ₀　　ρ₁＝０

　　　対立仮説：Ｈ₁    ρ₁≠０

   (2)検定統計量χ² を求める

　　　固有値：　λ₁＝0.9679  λ₂ ＝0.1243  標本数（ｍ）：10    変量数（ｐ）：2

     

 

　　　

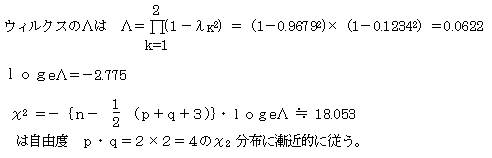
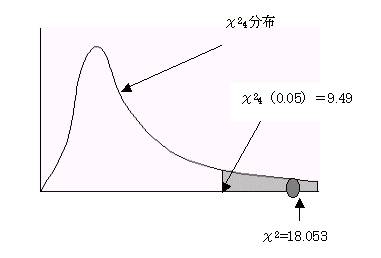
      χ²=18.053 ＞ χ²₄（0.05）＝9.49

　　　棄却域にはいる。帰無仮説を棄却する。よって対立仮説（Ｈ₁）：ρ1≠０を採択する。

　　　母集団における第１正準相関係数は０ではないといえる。

　

 

（２）母集団における第２正準相関係数の検定を行う

      母集団における第２正準相関係数をρ₂ とする。

　 (1)仮説をたてる

　　　帰無仮説：Ｈ₀　　ρ₂＝０

　　　対立仮説：Ｈ₁    ρ₂≠０

   (2)検定統計量χ² を求める

　　　固有値：　λ₁＝0.9679  λ₂ ＝0.1243  標本数（ｍ）：10    変量数（ｐ）：2

     

 

　　　　

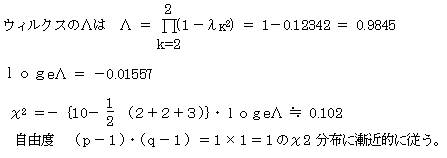
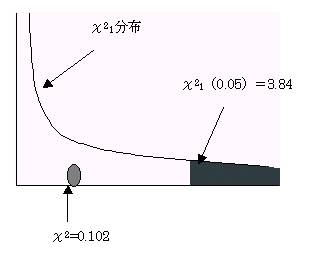
      χ²=0.102 ＜ χ²₁（0.05）＝3.84

　　　棄却域に入らない。よってρ₂＝０という帰無仮説を棄却できない。

  以上から、採用する正準相関係数は第１正準相関係数までとする。

  第１正準相関係数＝０．９６７９であり、今回実施した会社の営業力（知名度と販売力の合成した変量）と技術力（研究力と応用力の合成した変量）の相関は非常に高いと考えられる。