７． 正準相関分析
２つの量的変量ｘ1とｘ2がある時、この２変量間の関係を調べたいときには、２変量の標本を幾つか集め、その相関係数を求めることにより２変量間の関係の度合を調べることができる。しかし変量がｘ1・ｘ2・ｘ3の３変量になったとき、ｘ1・ｘ2の組とｘ3の関係をみたいとか、変量がｘ1・ｘ2・ｘ3・ｘ4の４変量で、ｘ1・ｘ2の組とｘ3・ｘ4の組の関係をみたいとき、そのままでは相関関係をみることができない。そこで、ｘ1・ｘ2の組とｘ3の関係をみたいときには、まずｘ1・ｘ2のデータを合成して、その合成した変量と
ｘ3との相関係数を求めて、関係をみるようにする。このようにｘ1・ｘ2を合成して得られる変量を正準変数と呼び、得られる相関係数を正準相関係数と呼ぶ。
７．１ 正準相関係数を求める。
いま下の表のように４変量（ｘ1・ｘ2・ｘ3・ｘ4）の標本データがあるとする。
|
標本NO |
Ｚ |
Ｗ |
||
|
ｘ1 |
ｘ2 |
ｘ3 |
ｘ4 |
|
|
１ ２ … ｎ |
ｘ11 ｘ12 … ｘ1n |
ｘ21 ｘ22 … ｘ2n |
ｘ31 ｘ32 … ｘ3n |
ｘ41 ｘ42 … ｘ4n |
変量ｘ1・ｘ2の組とｘ3・ｘ4の組がどれくらい関係があるかを調べる。
ｘ1・ｘ2を合成して得られる変量をＺ、ｘ3・ｘ4を合成して得られる変量をＷとすると、
Ｚ＝ｌ1･ｘ1＋ｌ2･ｘ2
Ｗ＝ｍ1･ｘ3＋ｍ2･ｘ4
この時、Ｚ・Ｗを正準変量といい、ｌ・ｍは正準変量の係数である。この正準変量ＺとＷの相関係数（正準相関係数）を最大にするような、ｌ・ｍを求める必要がある。
（合成変数間の関係をできるだけ残すように集約させなければならないので）
正準相関分析では、正準変量Ｗが１変量の時には、重回帰分析と同じとなる。また、正準変量Ｗが１変量で２群以上に分かれているときには、判別分析と同じとなる。
一般に、ｐ個の変数とｑ個の変数間には、ｐ・ｑ個の相関関係を求めることができるが、これはｐ個の正準相関に集約することができる。（但しｐ≦ｑ）
正準相関係数を求める。
Ｚ＝ｌ1･ｘ1＋ｌ2･ｘ2
Ｗ＝ｍ1･ｘ3＋ｍ2･ｘ4
この分散をＳZZ・ＳWW、共分散をＳZWとすると、ＺとＷの相関係数ｒZWは
合成変量ＺとＷのそれぞれの分散を１・平均を０と仮定する。標準化された変量ｘ1〜ｘ4を使用して、それぞれの分散共分散を求める。
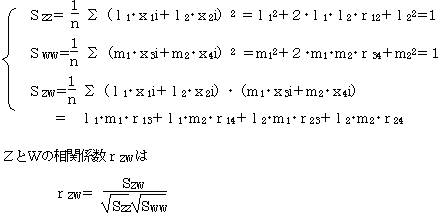
ＳZZ＝１、ＳWW＝１の条件下で、このｒZWを最大にするようなｌ･ｍを求める。
４変量ｘ1･ｘ2･ｘ3･ｘ4の単相関係数をみると
|
|
ｘ1 ｘ2 |
ｘ3
ｘ4 |
|
ｘ1 ｘ2 |
ｒ11
ｒ12 ｒ21
ｒ22 |
ｒ13 ｒ14 ｒ23 ｒ24 |
|
ｘ3 ｘ4 |
ｒ31
ｒ32 ｒ41
ｒ42 |
ｒ33 ｒ34 ｒ43 ｒ44 |
なおｒ11＝ｒ22＝ｒ33＝ｒ44＝1
ここで
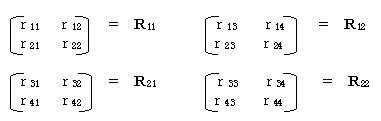
とおくと
前の表は
|
|
ｘ1 ｘ2 |
ｘ3 ｘ4 |
|
ｘ1 ｘ2 |
Ｒ11 |
Ｒ12 |
|
ｘ3 ｘ4 |
Ｒ21 |
Ｒ22 |
この固有方程式から、λ2を得る。第１正準相関は値の大きい方のλ値を採用する。
いま、λ1≧λ2 とすると、λ1を使用して固有ベクトルを求める。
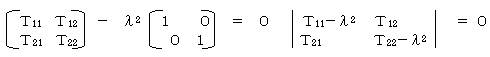
ＺとＷが正の相関があるときには正の固有値（λ）を採用し、負の相関があるときには負 の固有値を採用する。
また ｌ’･Ｒ11･ｌ＝１ であるから、これからｌ1とｌ2 を求める。
次に
これからｍ1とｍ2が求められる。
以上から正準変量ＺとＷは
Ｚ＝ｌ1･ｘ1＋ｌ2･ｘ2
Ｗ＝ｍ1･ｘ3＋ｍ2･ｘ4 の式を得る。また第１正準相関係数：λ1となる。
正準相関係数の個数は、ｐ個の変数とｑ個の変数があると（ｐ≦ｑとする）、ｐ個の正準相関係数を求めることができる。しかし、この全てを使用するとは限らない。そこで、母集団において有効な正準相関係数の個数を決めるための検定を行う。この検定をバートレットの検定という。
いま、ｐ個の変数とｑ個の変数があり（ｐ≦ｑ）、ｐ個の固有値（λ）が、
λ12≧λ22≧…≧λp2と得られたとする。
この時、「１番目からｋ番目までの固有値は０である。」という仮説下で、検定統計量をχ2 とすると、
検定統計量 χ2 ＝−｛ｎ−0.5×（ｐ＋ｑ＋3）｝･ｌｏｇe（Λ）
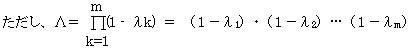
は、自由度ｐ･ｑのχ2 分布に漸近的に従う。
検定をおこなう。
(1)仮説をたてる
帰無仮説
Ｈ0：ρj＝０ （j＝1,2,…k）
（１からｋ番目迄の正準相関係数＝０）
対立仮説
Ｈ1：ρj≠０ （j＝1,2,…k）
（１からｋ番目迄の正準相関係数≠０）
(2)検定統計量χ2 は、自由度ｐ･ｑのχ2 分布に従う
(3)有為水準αで検定する
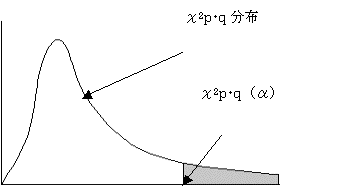
χ2 ≧χ2p･q であれば、仮説を棄却する。つまり、第１正準相関係数から第ｋ正準相関係 数まで、０ではない。
また、ｋ＋１番目の正準相関係数の検定については、
検定統計量 χ2k ＝−｛ｎ−０．５（ｐ＋ｑ＋３）｝・ｌｏｇe（Λk）
