11.@P³zuªUªÍ
3QÈãÌê½ÏÌ·Ìèðs¤ÉÍA2QÌê½ÏÌ·Ìèð»ÌgÝí¹ÌñªJèÔµÀsµÈ¯êÎÈçÈ¢B±Ìæ¤ÈÉ1ñÅè·éàÌÉuP³zuªUªÍvª éBªèf[^ÉÎç«ð^¦évöð1Âl¦éà̪uP³zuªUªÍvÅ èA2Âl¦éà̪uQ³zuªUªÍvÅ éB½¾µAef[^ÍÙÚ³KªzÉ]¢©ÂªUÅ éàÌÆ·éB
11.1@P³zuªUªÍ
éGßÌî̬çð3næŲ׽Bî̬·ÍnæÉæè·ª é©L× 5%Åèðs¤BÏ®vöÍnæÉæéá¢Å èA3QÌê½ÏÌ·ðè·éÌÅAP³zuªUªÍðÀs·éB
P³zuªUªÍÍAªUðÔÏ®iöqÔÏ®:næÉæéÏ®jÆàÏ®iöqàÏ®:¯ênæàÅÌÏ®jÆɪ¯ÄªUäðßAÔÏ®ªàÏ®æèàå«¢©èµAÔÏ®ªàÏ®æèà嫯êÎAê½ÏÉ·ª éÆ·éèÅ éBµ©µAÇÌQÔÅ·ª é©Ís¾Å éBÇÌQÔÅê½ÏÉ·ª é©ÍA{EtF[jÌû@âVFbtFÌû@ÈǪ éB
11.2@1³zuªUªÍÌÀ{
i1jW{f[^ðü͵Ac[ðgpµAP³zuªUªÍðÀs
W{f[^ÅWßçêÈ©Á½f[^Í»ÌÜÜóɵĨB
c[¨ªÍc[¨ªUªÍ:1³zuªUªÍðIð
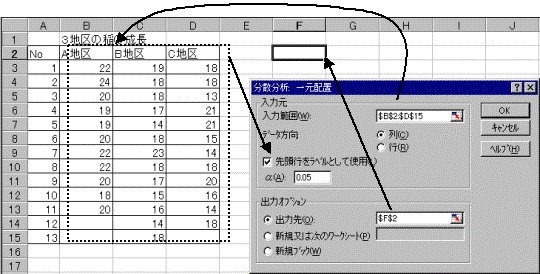
üÍÍÍÍAÚsiAnæEBnæECnæ̶ÌsjðÜßÄêxÌhbOµÄªÍ·éf[^ÍÍðwè·éBæªÌ¶ñÌsÍxƵÄgp·éÌÅAuæªsðxƵÄgpvÌðNbNµÄ`FbN·éBoÍæðwèµAOK{^ðNbN·éÆ·×ÉuP³zuªUªÍ\vªvZ³ê\¦³êéB
i2j쬳ê½u1³zuªUªÍ\vð¢·éB
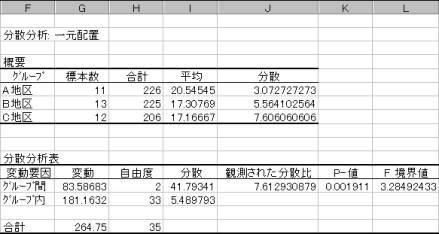

@ÔϮ̽ûaSAÍAeO[v̽ϪS½Ï©çÇêç¢Îç¢Ģé©Å éBe
iO[vjÅ̽ÏÆSW{̽ÏÆ̷̽ûaÉe
ÅÌW{ð©¯ÄßéB![]() @@ܽÔϮ̩RxÍA
(O[v)-1Å éB
@@ܽÔϮ̩RxÍA
(O[v)-1Å éB
AàϮ̽ûaSEÍAe
Ìf[^ªe
̽ϩçÇêç¢Îç¢Ģé©Å éBe
iO[vjÅ̽ÏÆef[^Æ̷̽ûaðe
ÅßA³çÉS
Åvµ½àÌÅ éB![]()
@ܽàϮ̩RxÍASW{- Å éB
BSϮ̽ûaSTÍAÔÏ®SAÆSEàÏ®ðÁ¦½àÌÅ éBܽSϮ̩RxÍAÔϮ̩Rx+àϮ̩RxÅ éB
èvÊͪUä(F): ![]() Å èA©RxfA,fEÌFªzÉ]¤B
Å èA©RxfA,fEÌFªzÉ]¤B
(3)èðÀ{
@¼àð½Äé
A³¼à@H0:ÔÏ®ÍøʪȢiVAàVE)
Χ¼à@H1:ÔÏ®Íøʪ éiVAVEj
AèvÊiFjðßé
@èvÊ(F): ![]() =7.612930879@Í©Rx2,33ÌF2,33ªzÉ]¤
=7.612930879@Í©Rx2,33ÌF2,33ªzÉ]¤
BL×m¦5%ÅãФèðÀ{(VAVEÌèÅ é©çEФèðÀ{)
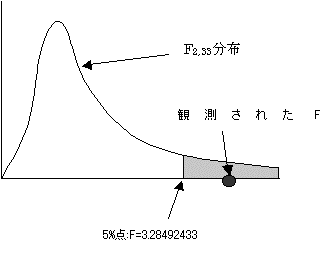
F2,33ªzÌ5%_Í3.28492433Å éBϪ³ê½FlÍ7.612930879Å èA±ÌlÍ5%_Flæèàå«¢BܽÂÌÌm¦:0.001911Å è±ÌlÍ0.05æ謳¢B±ê©çA³¼àðüp·éBÔÏ®Íøʪ éÆ¢¦éB3QÌê½ÏÉ·ª éÆ¢¦éBî̬·ÍnæÉæè·ª éÆ¢¦éBµ©µÇÌnæÔÅê½ÏÉ·ª é©s¾Å éB
12.@JèÔµÌÈ¢2³zuªUªÍ
3QÈãÌê½ÏÌ·ÌèðÀ{·éA»Ìf[^ªÙÚ³KªzÉ]¢©ÂÎç«ð^¦évöª2Â(ÔÏ®ð2Â) éðl¦éB½¾µAöqÌgÝí¹ÉæèÎç«ɽç©ÌøÊð^¦éðÝìp(¨Ý¢Ée¿ð^¦éìp)ªÈ¢Æ·éB±ÌðÝìpªFßçêéÉÍAJèÔµÌ é2³zuªUªÍðÀ{·éB
12.1@JèÔµÌÈ¢2³zuªUªÍ
jÊÆ7ÂÌÆEÊÉC𲸵½Æ±ëAºÌæ¤ÈÊð¾½B±Ìf[^©çCÌ^ÍÆEÔÅ·Ùª é©AܽjÔÅ·Ùª é©AL×m¦5%ÅèðÀ{·éBCÉÎç«ð^¦évöÍ2 éB1ÂÍÆEÔÌá¢Å èA¼Ì1ÂÍjÔÌá¢Å éBJèÔµÌÈ¢2³zuªUªÍÍA1³zuªUªÍƯlÉASªUðÔÏ®ÆàÏ®Æɪ¯AÔÏ®ªàÏ®æèå«¢©Ç¤©èðs¤B
12.2@JèÔµÌÈ¢2³zuªUªÍÌÀ{
(1)f[^ðüÍ·éB
(2)c[ðgpµAJèÔµÌÈ¢2³zuªUªÍðÀ{
c[¨ªÍc[¨ªUªÍ:JèÔµÌÈ¢2³zuðIð
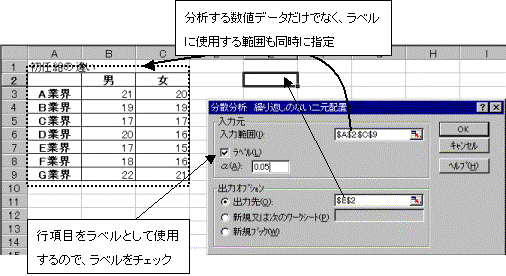
ªÍÉgp·éf[^ðÍÍwèµAOK{^ðNbN·éƪÍʪ\¦³êéB
(3)ªÍÊð¢
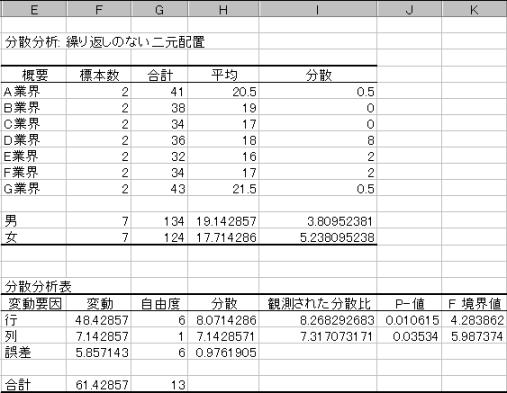

@SÏ®(T)̽ûaÍ(ST)ASf[^ªS½Ï©çÇêç¢Îç¢Ģé©Å éB
![]() ÆÂXÌf[^(Xij)·Ì½ûaÅßéB
ÆÂXÌf[^(Xij)·Ì½ûaÅßéB![]()
AÔÏ®(A)̽ûaSAÍAe
(ÆE)Å̽ϪS½Ï©çÇêç¢Îç¢Ģé©Å éBe
iÆEjÅ̽ÏÆSW{̽ÏÆ̷̽ûaÉe
ÅÌW{𩯽ßéB![]()
ܽÔÏ®(SA)Ì©RxÍA (ÆE)-1Å éB
BÔÏ®(B)̽ûaSBÍAe
(j)Å̽ϪS½Ï©çÇêç¢Îç¢Ģé©Å éBe
ijjÅ̽ÏÆSW{̽ÏÆ̷̽ûaÉe
ÅÌW{𩯽ßéB![]()
ܽÔÏ®(SB)Ì©RxÍA (j)-1Å éB
CàϮ̽ûaSEÍASE=ST-SA-SB©çßéB
(3)èðÀ{
(3-1)ÔÏ®A(ÆEÔÌ·Ù)Íøʪ é©è·é
@¼àð½Äé
A³¼à@H0:ÔÏ®AÍøʪȢiVAàVE)
Χ¼à@H1:ÔÏ®AÍøʪ éiVAVEj
AèvÊiFjðßé
@èvÊ(F):FA@=@![]() @=@8.268292683@Í©RxfA,fE(6,6)ÌFªzÉ]¤
@=@8.268292683@Í©RxfA,fE(6,6)ÌFªzÉ]¤
BL×m¦5%ÅãФèðÀ{
Ϫ³ê½Fl:8.268ÍAF6,6(0.05):4.2838æèàå«¢Bܽ±ÌÌm¦:0.00106Í0.05æèଳ¢AæÁÄüpæÉüéBA³¼àðüp·éBÔÏ®AÍøʪ éÆ¢¦éBÆEÔÅCÉᢪ éÆ¢¦éB
(3-2)ÔÏ®B(jÔÌ·Ù)Íøʪ é©è·é
@¼àð½Äé
A³¼à@H0:ÔÏ®BÍøʪȢiVBàVE)
Χ¼à@H1:ÔÏ®BÍøʪ éiVBVEj
AèvÊiFjðßé
@![]() Í©RxfB,fE(1,6)ÌFªzÉ]¤
Í©RxfB,fE(1,6)ÌFªzÉ]¤
BL×m¦5%ÅãФèðÀ{
Ϫ³ê½Fl:7.31707ÍAF1,6(0.05):5.98737æèàå«¢Bܽ±ÌÌm¦:0.003534Í0.05æèଳ¢AæÁÄüpæÉüéBA³¼àðüp·éBÔÏ®BÍøʪ éÆ¢¦éBjÔÅCÉᢪ éÆ¢¦éB
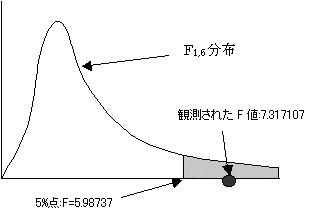
12.3@ðÝìpÌ¢
JèÔµÌÈ¢2³zuªUªÍÅÍAðÝìpÌL³ÍmFÅ«È¢BðÝìpÌL³É¢ÄÍAJèÔµÌ é2³zuªUªÍðÀ{·éKvª éBJèÔµÌÈ¢2³zuªUªÍðÀ{µÄAðÝìpªFßçêé©Ç¤©ÍAOtð`¢ÄÝéÆÂ\«ÌL³ªª©éBOtÌ¡²É AiO[vA:ÆEjðÆèAc²ÉCÌlðÆèA aijjÌ^ðüOtÉ쬷éB±ÌOtª½µ½èð·µ½èµÄ¢éÉÍAðÝìpª éÂ\«ª éB
Otð`ÆA2Â̼üÍð·àȽàµÄ¢È¢ÌÅAðÝìpÍÈ¢àÌÆvíêéB
13.@JÔµÌ é2³zuªUªÍ
ªèf[^ÉÎç«ð^¦évöð2Âl¦éB±Ì2ÂÌvöÉÂ¢Ä¢Â©Ì (O[v)ɪ¯¡ñf[^ðªè·éB2ÂÌvöÉ¢Ļê¼êøʪ é©Aܽ2ÂÌöqÔÉðÝìpª é©ðè·éB
13.1@JÔµÌ é2³zuªUªÍ
4ÐÌA¨ÌíqÌèóµð_ògpEL@Í|E³_òÌ3íÞɪ¯Ä3ñ¸ÂϪµ½BA¨ÌèóµÉ¢ÄA A(O[vAFïÐÌá¢)Æ BiO[vB:Í|û@Ìá¢jÉæèAèóµÉᢪ é©Ü½öqÔÌðÝìpÍ é©ðAL×m¦5%Åèðs¤B
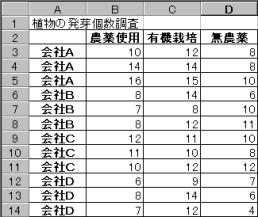
(1)f[^ðüÍ
f[^Í A(ïÐÊ)ðcûüÉA B(Í|û@Ìá¢)¡ûüÉÆèAA±µÄ3ñ¸ÂÌf[^ðü͵ĢB
(2)c[ðgpµAJèÔµÌ é2³zuªUªÍðÀ{
c[¨ªÍc[¨ªUªÍ:JèÔµÌ é2³zuðIð
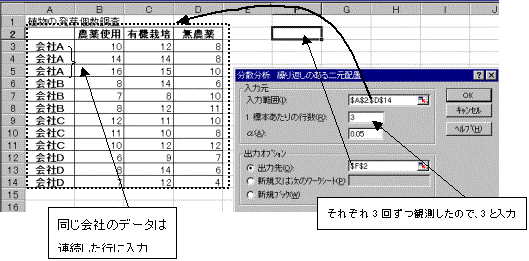
ªÍÉgp·éf[^ðÍÍwèµAOK{^ðNbN·éÆ·®ÉªÍʪ\¦³êéB
(3)ªÍÊð¢
ºÌæ¤ÈªÆCʪ\¦³êéB
|
ªUªÍ: JèÔµÌ éñ³zu |
|
|
|
|
|||||||
|
Tv |
_ògp |
L@Í| |
³_ò |
v |
|
|
|||||
|
ïÐ` |
|
|
|
|
|
|
|||||
|
W{ |
3 |
3 |
3 |
9 |
|
|
|||||
|
v |
40 |
41 |
26 |
107 |
|
|
|||||
|
½Ï |
13.33333 |
13.66667 |
8.666667 |
11.88888889 |
|
|
|||||
|
ªU |
9.333333 |
2.333333 |
1.333333 |
9.111111111 |
|
|
|||||
|
ïÐa |
|
|
|
|
|
|
|||||
|
W{ |
3 |
3 |
3 |
9 |
|
|
|||||
|
v |
23 |
34 |
27 |
84 |
|
|
|||||
|
½Ï |
7.666667 |
11.33333 |
9 |
9.333333333 |
|
|
|||||
|
ªU |
0.333333 |
9.333333 |
7 |
6.75 |
|
|
|||||
|
ïÐb |
|
|
|
|
|
|
|||||
|
W{ |
3 |
3 |
3 |
9 |
|
|
|||||
|
v |
33 |
33 |
30 |
96 |
|
|
|||||
|
½Ï |
11 |
11 |
10 |
10.66666667 |
|
|
|||||
|
ªU |
1 |
1 |
4 |
1.75 |
|
|
|||||
|
ïÐc |
|
|
|
|
|
|
|||||
|
W{ |
3 |
3 |
3 |
9 |
|
|
|||||
|
v |
21 |
35 |
17 |
73 |
|
|
|||||
|
½Ï |
7 |
11.66667 |
5.666667 |
8.111111111 |
|
|
|||||
|
ªU |
1 |
6.333333 |
2.333333 |
9.861111111 |
|
|
|||||
|
v |
|
|
|
|
|
|
|||||
|
W{ |
12 |
12 |
12 |
|
|
|
|||||
|
v |
117 |
143 |
100 |
|
|
|
|||||
|
½Ï |
9.75 |
11.91667 |
8.333333 |
|
|
|
|||||
|
ªU |
9.295455 |
4.628788 |
5.515152 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
ªUªÍ\ |
|
|
|
|
|
|
|||||
|
Ï®vö |
Ï® |
©Rx |
ªU |
Ϫ³ê½ªUä |
P-l |
F «El |
|
||||
|
W{ |
72.22222 |
3 |
24.07407 |
6.37254902 |
0.002483 |
3.008786 |
|
||||
|
ñ |
78.16667 |
2 |
39.08333 |
10.34558824 |
0.000575 |
3.402832 |
|
||||
|
ðÝìp |
50.94444 |
6 |
8.490741 |
2.24754902 |
0.073123 |
2.508187 |
|
||||
|
JèÔµë· |
90.66667 |
24 |
3.777778 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
v |
292 |
35 |
|
|
|
|
|||||
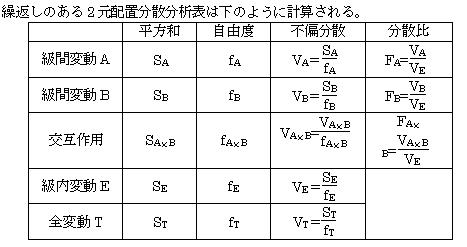
ÅÉe ²ÆÌW{¥v¥½Ï¥ªUªvZ³êÄ\¦³êA±¯ÄªUªÍ\ª\¦³êéBªUªÍ\ðÝÄèðÀ{·éB
(4)èðÀ{
(4-1)ÔÏ®A(ïÐÔÌ·Ù)Íøʪ é©è·é
@¼àð½Äé
A³¼à@H0:ÔÏ®AÍøʪȢiVAàVE)
Χ¼à@H1:ÔÏ®AÍøʪ éiVAVEj
AèvÊiFjðßé
@![]() @Í©RxfA,fE(3,24)ÌFªzÉ]¤
@Í©RxfA,fE(3,24)ÌFªzÉ]¤
BL×m¦5%ÅãФèðÀ{
Ϫ³ê½Fl:6.37254902ÍAF3,24(0.05):3.008786æèàå«¢Bܽ±ÌÌm¦:0.002483Í0.05æèଳ¢AæÁÄüpæÉüéBA³¼àðüp·éBÔÏ®AÍøʪ éÆ¢¦éBïÐÔÅA¨ÌíqÌèóµÉᢪ éÆ¢¦éB
(4-2)ÔÏ®B(Í|û@Ìá¢)Íøʪ é©è·é
@¼àð½Äé
A³¼à@H0:ÔÏ®BÍøʪȢiVBàVE)
Χ¼à@H1:ÔÏ®BÍøʪ éiVBVEj
AèvÊiFjðßé
@![]() @Í©RxfB,fE(2,24)ÌFªzÉ]¤
@Í©RxfB,fE(2,24)ÌFªzÉ]¤
BL×m¦5%ÅãФèðÀ{
Ϫ³ê½Fl:10.34558824ÍAF2,24(0.05):3.402832æèàå«¢Bܽ±ÌÌm¦:0.000575Í0.05æèଳ¢AæÁÄüpæÉüéBA³¼àðüp·éBÔÏ®BÍøʪ éÆ¢¦éBÍ|û@Ìá¢ÉæèA¨ÌíqÌèóµÉᢪ éÆ¢¦éB
(4-2)ðÝìpÍøʪ é©è·é
@¼àð½Äé
A³¼à@H0:ðÝìpÍøʪȢiVA~BàVE)
Χ¼à@H1:ðÝìpÍøʪ éiVA~BVEj
AèvÊiFjðßé
@![]() @Í©RxfA~B,fE(6,24)ÌFªzÉ]¤
@Í©RxfA~B,fE(6,24)ÌFªzÉ]¤
BL×m¦5%ÅãФèðÀ{
Ϫ³ê½Fl:2.24754902ÍAF6,24(0.05):2.508187æèଳ¢Bܽ±ÌÌm¦:0.073123Í0.05æèàå«¢AæÁÄüpæÉüçÈ¢BA³¼àðüp·éÍÅ«È¢BðÝìp©øʪȢðüpÅ«È¢B
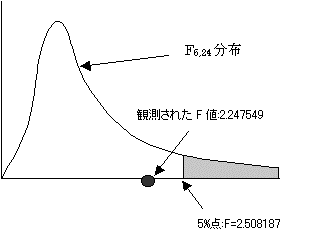
Èã©çíqÌèóµÍAïÐÔÅ·Ùª èܽÍ|û@Åà·ÙªFßçêéBµ©µA 1(ïÐÔÌá¢)Æ 2(Í|û@Ìá¢)Æ¢¤2ÂÌöqÔÌðÝìpÍøʪȢƢ¤¼àÍüpÅ«È¢B
(5)v[O
@ðÝìpÉøʪȢƻ¾µ½ÉÍAðÝìpÌÏ®ðàÏ®Év[iêÉ·éjµÄÄx2³zuªUªÍðÀ{·é̪]ܵ¢B
v[µ½ãÌàÏ®E'̽ûaðSE'ܽ©RxðfE'Æ·éÆ
½ûaÍSE'=SE+SA~B@©RxÍfE'=fE+fA~BÆÈéB![]()
±êÉæèv[OãÌ
A̪Uä(FA')ÍA![]()
v[OãÌ
B̪Uä(FB')ÍA![]()
Èã©çv[Oµ½ãÌ2³zuªUªÍ\ð쬷éÆ
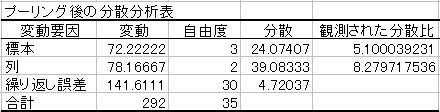
v[Oµ½ã̪Uäðp¢ÄÄxèðÀ{
v[OãÌ A̪Uä:@@©RxÍ3Æ30
v[OãÌ B̪Uä:8.279717@©RxÍ2Æ30
±ê©çFªzÉÖ·éÖðgpµÄm¦ðßéB
AFF3,30=5.10039@Í0.005693@@ BFF2,30=8.279717@Í0.005693
±ÌlÍ¢¸êà0.05æ謳¢BæÁÄüpæÉüéBv[ãàüpæÉüéÌÅA AE BÆàÉøʪ éÆ¢¦éB

14.@2ÏÊÔÉÖ·éªÍ
14.1@2ÏÊÔÌÖ
2ÏÊiX¥Y)Ôɽç©ÌÖWª é©ð²×éBÏÊXÆ»êÉ˶·éÏÊYª èA±ÌXEYÌyAÉÈÁÄ¢éf[^ªn éA±Ì2ÏÊXEYÔÌÖWªÇêç¢ é©ð²×éB¢ÜlÔÌg·ÆÌdÌf[^Ôɽç©ÌÖWª é©ð²×éBg·àÌdà³KªzÉ]¤f[^Å éB2ÏÊÔŽç©ÌÖWª é©ð²×éÉÍAuUz}ð쬷év¨uÖWðßévÌÔÉÀsµAÖÖWð²×éB
14.1.1@Uz}Ìì¬
2ÏÊÌÖWðoIÉ\¦µAÇÌæ¤ÈÖWª é©ð²×éB
10lÌw¶ªêÆw̱ðó¯½B»ÌʪºÌæ¤ÉÈÁ½AêÌ_ÆwÌ_Ôɽç©ÌÖWª é©ð²×éB
¡²ÉêÌ_Ac²ÉwÌ_ðÆèA10lÌw¶Ì_ðY·éÊuÉvbgµÄ¢B(Uz}ð쬷é)
@EXCELÉÍOtì¬@\ª éÌÅA±êðpµÄUz}ð쬷éB

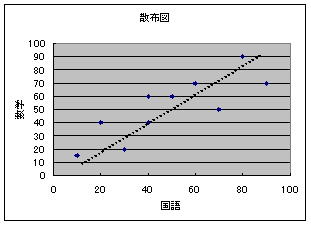 쬳ê½Uz}
쬳ê½Uz}
쬳ê½Uz}ð©éÆAEãªè̼üóÉf[^ªÀñÅ¢éXüª éBêÌ_ªÈêÎAwÌ_àÈéXüÉÈÁÄ¢éB±Ìæ¤ÈA³ÌÖª éÆ¢¤Bܽ±ÌtÉEºªè̼üÌXüª éÉÍAÌÖª éÆ¢¤Bf[^ª½ç©Ì¼üóÌXüð¦³È¢ÍA֪ȢƢ¤B
Uz}ð쬵½AºÌæ¤ÈXüª©çê½A»ê¼ê³ÌÖEÖ³µEÌÖÆ¢¤B
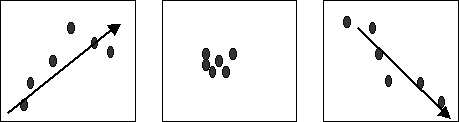
u³ÌÖ:EãªèÌXüvuÖ³µ:½XüȵvuÌÖ:EºªèÌXüv
14.1.2@ÖW
Uz}ð쬵½ÊAEãªèEEºªèÌæ¤ÈXüª©çê½ÉÍA2ÏÊÔɽç©ÌÖª 軤ÈÌÅAÇêç¢ÌÖª é©ðuÖWvðßÄB»Ìx¢ðmF·éB
ÖWðrÆ·éÆAÖWÍ-1 r +1ÌÍÍÌlðÆéB
rª-1ÉߢÙÇÌÖª¢Brª+1ÉߢÙdzÌÖª¢Bܽrª0ÉߢÙÇ֪ȢB
(1)c[ðgpµÄÖWðßé
c[¨ªÍc[¨ÖÆIðµAÖWðßéQÏÊÌÍÍðwè
ÅãÉOK{^ðNbN·éÆAÖWsñª\¦³êéB


êÌf[^ÆwÌf[^ÌÖW:0.826305Æßçê½B±ÌlÍ+1ÉߢÌÅA¢³ÌÖª éÆ¢¦éB
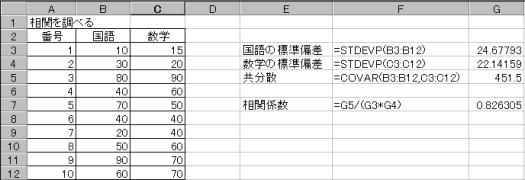
(2)ÖðgpµÄÖWðßéB
ÖWðßéÖccorrel(Ï1ÍÍ,Ï2ÍÍ)

(3)WηE¤ªUðp¢ÄÖWðßéB
ÏÊXÌêWcÉηéWηðÂxAÏÊYÌêWcÉηéWηðÂyA2ÏÊ(X,Y)̤ªUðSxyÆ·éAÖW(r)ÍA![]() ÅßçêéB
ÅßçêéB
êWcÉηéWηðßéÖ: =stdevp(ÏÍÍ)
2ÏÊ(X,Y)̤ªUðßéÖ: =covar(Ï1ÍÍ,Ï2ÍÍ)
15. PñAªÍ
15.1@PñA®ðßéB
2ÏÊÔÉÖª éA±Ì2ÏÊÔÉü`ñA¼üðl¦éB
ü`ñA¼üð:Y=b1x+b0ƵÄAÀf[^Ʊ̼üÆÌc·ðÃÆ·éBY=b1x+b0̼üÍA·×ÄÌW{f[^É¢ÄA»Ìc·ªÅ¬ÉÈéæ¤ÉÝè·éKvª éB±Ì¼ü©çeW{f[^Æ̸êïðvé½ßÉAec·Ì½ûaðÆèA±Ìc·½ûaªÅ¬ÉÈéæ¤É·éB±Ìæ¤Èû@ðŬ2æ@Æ¢¤BW{f[^ÍA¼ü:Y=b1x+b0©çc·(Ã)¸êÄ¢éÌÅAy=b1x+b0+ÃÆ\·B±ê©çü`ñAfðyi=À1xi+À0
+Ãi@(i=1,2,cn)Æ·éB
c·(Ã)É¢Ä
@ÃiÆÃjͨݢÉƧŠèA³KªzN(0,Â2)É]¤B
AÃiÌúÒl(½Ïl)Í0Å èAܽªUÍêèÅ éB
̼èºÅAPñA®ðY=b1x+b0Æ·éÆAb1,,b0ÍÀ1,À0ÌèÊÅ éB
c·ÉÚµAÃi=yi-Yi@©ç@Ãi=yi-b1¥xi-b0@±Ìc·ð·×ÄÌW{É¢ÄvµA»ÌvðŬɷéæ¤Èb1¥b0ðßéÆAPñA®ªßçêéB

°(Ãi)2=°(yi-b1¥xi-b0)2@@f=°(yi-b1¥xi-b0)2@Ƶ½A±ÌfðŬɷéb1¥b0ðßAPñA®ðßéB
15.2@à¾ÏÊÆÚIÏÊ
@êÌ_ðXAwÌ_ðYÆ·éBêÌ_ÆwÌ_ÔÉͳÌÖª èAêÌ_ªÈéÆAwÌ_ªÈéBwÌ_(Y)ÍêÌ_(X)É˶µÄ¢éB±Ìæ¤É2ÏÊÔɼüIÈÖWªFßçêéB±Ì¼üðvZµÄßéÆPñA®ªßçêéB±ÌPñA®ðp·éÆAêÌ_©çwÌ_ð\ª·é±ÆªÅ«éB¢Ü\ªµÄßéÌÍuwvÌ_Å èA»Ì\ªÌ³ÆÈéÌÍuêvÌ_Å éB±Ìæ¤ÉßéÏÊðuÚIÏÊܽÍ]®ÏÊvÆÄÑA»Ì\ªÌàÆÆÈéÏÊðuà¾ÏÊܽÍƧÏÊvÆ¢¤BÚIÏÊÍíÉ1ÂÅ èAà¾Ïʪ1ÂÌðuPñAªÍvÆÄÑAà¾Ïʪ2ÂÈãÌðudñAªÍvÆ¢¤B
15.3@PñAªÍðÀ{
15.3.1@ªÍc[ðgpµPñAªÍÀ{
(1)ªÍ·éf[^ðü͵Ac[¨ªÍc[¨ñAðIð·éB
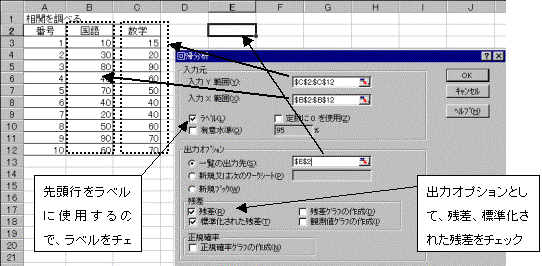
@üÍYÍÍÍAÚIÏÊÌÍÍðwè·éBæªsðxƵÄgp·éÍA¶ÌüÁ½ÚsàÍÍÉüêéB
AüÍXÍÍÍAà¾ÏÊÌÍÍðwè·éBæªsðxƵÄgp·éÍAüÍYÍÍƯlÉwè·éB
BªÍÍÍÌæªsðxƵÄgp·éÍAxÌðNbNµÄ`FbNB
CoÍæÍAªÍÊð\¦·éæªÌZÊuðwèB
DoÍIvVƵÄAc·AW»³ê½c·ðNbNµÄ`FbNB
ÈãðµÄ²OK{^ðNbN·éÆ·®ÉªÍʪ\¦³êéB
(2)ªÍÊð²×é
ºÌæ¤ÈªÍÊð¾çêéB
|
Tv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dÖ R |
0.826305 |
|
|
|
|
|
|
|
|
dè R2 |
0.68278 |
|
|
|
|
|
|
|
|
â³ R2 |
0.643127 |
|
|
|
|
|
|
|
|
Wë· |
13.94262 |
|
|
|
|
|
|
|
|
Ϫ |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ªUªÍ\ |
|
|
|
|
|
|
|
|
|
|
©Rx |
Ï® |
ªU |
Ϫ³ê½ªUä |
LÓ F |
|
|
|
|
ñA |
1 |
3347.328 |
3347.328 |
17.21907 |
0.003211 |
|
|
|
|
c· |
8 |
1555.172 |
194.3966 |
|
|
|
|
|
|
v |
9 |
4902.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
Wë· |
t |
P-l |
ºÀ 95% |
ãÀ 95% |
ºÀ 95.0% |
ãÀ 95.0% |
|
ØÐ |
15.17241 |
9.802094 |
1.547875 |
0.160242 |
-7.43127 |
37.7761 |
-7.43127 |
37.7761 |
|
ê |
0.741379 |
0.178663 |
4.149587 |
0.003211 |
0.32938 |
1.153378 |
0.32938 |
1.153378 |
|
|
|
|
|
|
|
|
|
|
|
c·oÍ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ϫl |
\ªl: w |
c· |
Wc· |
|
|
|
|
|
|
1 |
22.58621 |
-7.58621 |
-0.57711 |
|
|
|
|
|
|
2 |
37.41379 |
-17.4138 |
-1.32472 |
|
|
|
|
|
|
3 |
74.48276 |
15.51724 |
1.180447 |
|
|
|
|
|
|
4 |
44.82759 |
15.17241 |
1.154215 |
|
|
|
|
|
|
5 |
67.06897 |
-17.069 |
-1.29849 |
|
|
|
|
|
|
6 |
44.82759 |
-4.82759 |
-0.36725 |
|
|
|
|
|
|
7 |
30 |
10 |
0.760733 |
|
|
|
|
|
|
8 |
52.24138 |
7.758621 |
0.590224 |
|
|
|
|
|
|
9 |
81.89655 |
-11.8966 |
-0.90501 |
|
|
|
|
|
|
10 |
59.65517 |
10.34483 |
0.786965 |
|
|
|
|
|
(2-1)ñAWÉÖ·éªÍÊð¢
|
ñAv |
|
|
dÖ R |
0.826305 |
|
dè R2 |
0.68278 |
|
â³ R2 |
0.643127 |
|
Wë· |
13.94262 |
|
Ϫ |
10 |
@dÖR
dÖRÆÍAdÖWÅ èAÚIÏÊY(ÀÛÌwÌ_)ÆñA®æè¾çê½\ªlY'(ñA®©ç¾çê½wÌ\ª_)Ì2ÏÊÔÌÖW̱ÆÅ éBR=0.826305Å èA2ÏÊÔÌÖÍ©Èè¢Æ¢¦éBà¾ÏÊ(êÌ_)ÆÚIÏÊ(wÌ_)ÔÌÖWÅÍÈAÚIÏÊÆ\ªlÏÊÆÌÖÅ éB
AdÖR2
Àªf[^ÍAPñA¼üÌÜíèÉÎç¢ÄUݵĢéB±ÌÎç«̬³¢ÙÇPñA®Ì ÄÍÜèªÇ¢(¸xª¢)¼üÆ¢¦éBܽà¾ÏÊ(X)ÌÚIÏÊ(Y)É^¦ée¿ªå«¢Æ¢¦éBÂÜèèͪ嫢Ƣ¦éÌÅAR2ðèWÆࢤB

ñA¼ü
Bâ³R2
èWâdÖWÍAà¾ÏÊÌÂðâµÄ¢ÆPÉå«ÈéXüª éB»±ÅAPÉà¾ÏÊÌðâµÄàAèWªå«ÈçÈ¢æ¤É²®µ½àÌÉ©Rx²®ÏÝèW(â³R2)ª éB

(2-2)ñA®ÌM«ðè
(2-2.1)@ªUªÍ\ðgp·éû@
ñA®ðgpµÄAà¾ÏÊ©çÚIÏÊÌlð\ª·éA»Ì\ªlªÇêç¢M«ª éÌ©ðè·éû@ÉAªUªÍ\ðgp·éû@ª éBªUªÍ\ÅÍASÏ®(ST)ðñAæéÏ®(SR)Æc·ÉæéÏ®(SE)Æɪ¯AñAÉæéÏ®(SR)ªc·ÉæéÏ®(SE)æèଳ¯êÎAñA¼üÅß½\ªlÍAc·Éæée¿Ìûªå«¢ÌÅ\ªÉÍð§½È¢Æ·éû@Å éBÀªlÌÏ®(ST)=ñAÉæéÏ®(SR)+c·ÉæéÏ®(SE)B
c·ª¬³¢ÙÇAÀªlÌÏ®(ST)àñAÉæéÏ®(SR)ÆÈèAÇ¢\ªlð¾çêéB
PñAÌ̪UªÍ\ͺÌæ¤ÉÈéB
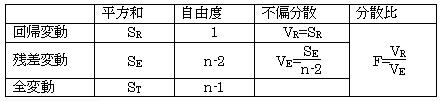
![]() ©Rx1,n-2ÌFªzÉ]¤BVRªVEæèàå«¢©è·éÌÅAEФèðÀ{·éB
©Rx1,n-2ÌFªzÉ]¤BVRªVEæèàå«¢©è·éÌÅAEФèðÀ{·éB
|
ªUªÍ\ |
|
|
|
|
|
|
|
©Rx |
Ï® |
ªU |
Ϫ³ê½ªUä |
LÓ F |
|
ñA |
1 |
3347.328 |
3347.328 |
17.21907 |
0.003211 |
|
c· |
8 |
1555.172 |
194.3966 |
|
|
|
v |
9 |
4902.5 |
|
|
|
@¼àð½Äé
A³¼à@H0:ñA¼üÍ\ªÉð§½È¢((VRàVE)
Χ¼à@H1:ñA¼üÍ\ªÉð§Â(VR>VE)
AèvÊ(F)ð²×é
![]()
BL× 5%ÅEФèðÀ{
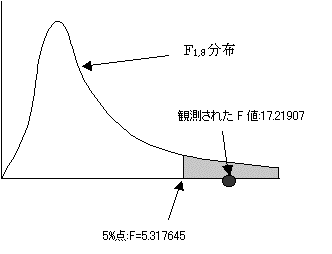
©Rx1,8Ìã¤0.05%ÍÖðgpµÄA=FINV(0.05,1,8)=5.317645ÆvZ³êéB
Ϫ³ê½FlÍAF1,8(0.05)=5.317645æèàå«¢BܽÂÌÌm¦:0.003211Å èA±ÌlÍ0.05æèଳ¢BæÁÄüpæÉüéBA³¼àðüp·éBñA®Í\ªÉð§ÂÆ¢¦éB
(2-2-2)@èWðgp·éû@
èWiR2)ðgpµÄAñA®ÌèðÀ{·éBèWð©éÆASÏ®ÉηéñAϮ̪ª©éÌÅA±Ìlªå«¢ÙÇñA®ÌM«Í¢Æ¢¦éBSÏ®ÉèßéñAÏ®ªR2% éÆ¢¦éB

(2-3)@ÎñAWÆYØÐÌM«ðè
ñA®©ÌͪUªÍÌÊM«ª éÆ»¾µ½BPñA®ÍAY=b1x+b0Å\³êéB±Ìb1ðÎñAWÆÄÑAb0ðYØÐÆ¢¤B±ÌÎñAWÆYØЪMÅ«é©èðs¤B
@Wë·(SE:Standard Error)
Wë·(SE)ÆÍAèlÌWη(SD)ð¢¤B
à¾ÏÊ(X)¥Àªl(y)¥\ªl(Y)¥c·(Ã)¥c·½û(Ã2)ÌÖWð\É·éB

|
|
W |
Wë· |
t |
P-l |
ºÀ 95% |
ãÀ 95% |
ºÀ 95.0% |
ãÀ 95.0% |
|
ØÐ |
15.17241 |
9.802094 |
1.547875 |
0.160242 |
-7.43127 |
37.7761 |
-7.43127 |
37.7761 |
|
ê |
0.741379 |
0.178663 |
4.149587 |
0.003211 |
0.32938 |
1.153378 |
0.32938 |
1.153378 |
à¾ÏÊ(ê)ÌWë·ÍAãÌvZ®©ç0.178663BܽYØÐÌWë·F9.802094ÆvZ³êßçêÄ¢éB
(2-3-1)@ÎñAW(b1)ÌM«ðè·éB
@¼àð½Äé
A³¼à@@H0:À10@(à¾ÏÊXÌêñAWÍ0Å éj
Χ¼à@@H1:À10@(à¾ÏÊXÌêñAWÍ0ÅÍÈ¢j
AèvÊ(T)ðßé
![]()
BL× 5%ż¤èðÀ{
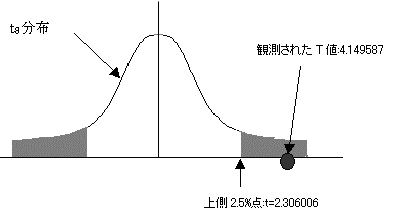
©Rx8Ìtªzã¤0.025_Í=tinv(0.05,8)=2.306006Å éBϪ³ê½tl:4.149587ͱÌlæèàå«¢Bܽ±ÌÌm¦:0.003211Å è0.05æèଳ¢BæÁÄüpæÉüéBA³¼àðüp·éBÎñAW(b1)Í\ªÉð§ÂÆ¢¦éB
(2-3-2)@YØÐ(B0)ÌM«ðè·éB
@¼àð½Äé
A³¼à@@H0:À00@
Χ¼à@@H1:À00@
AèvÊ(T)ðßé

BL× 5%ż¤èðÀ{
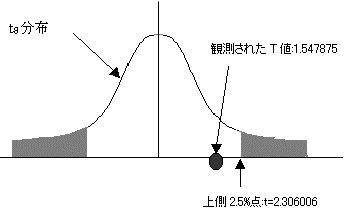
©Rx8Ìtªzã¤0.025_Í=tinv(0.05,8)=2.306006Å éBϪ³ê½tl:1.547875ͱÌlæèଳ¢Bܽ±ÌÌm¦:0.160242Å è0.05æèàå«¢BæÁÄüpæÉüçÈ¢BA³¼àðüp·é±ÆÍÅ«È¢BYØÐ(b0)Í\ªÉð§½È¢Æ¢¤A³¼àðüpÅ«È¢B
Èã©çAñA¼ü©ÌÍ\ªÉð§ÂÆ¢¦éBܽÎñAW(b1)Í\ªÉð§ÂªAYØÐ(b0)Í\ªÉð§ÂÆÍ¢¦È¢B
(2-4)@ñA®ðgpµ½\ªl
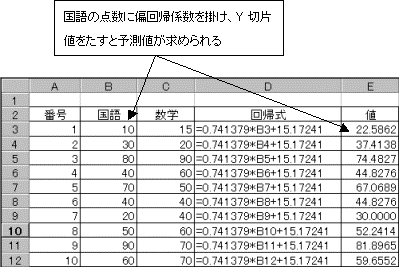
ñAªÍÉæèßçê½PñA\ª®ÍAY=0.741379x+15.17241Å éB±Ì®ðp¢ÄAêÌ_©çwÌ_ð\ª·éB
x:êÌ_Å é©çA±ÌêÌlðüêÄwÌ_YðvZµÄßéBȨAªÍc[ÅÍA±Ì\ªlàvZ³êÄ\¦³êÄ¢éB
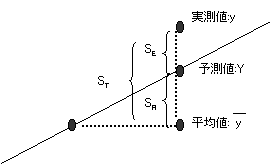
(2-5)@c·ð²×é
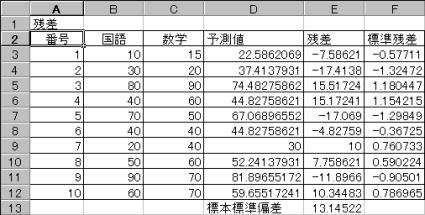
c·(Ã)ÍAÀªl(y)Æ\ªl(Y)Ì·Å éBÃi=yi-Yi
±Ìc·ðW»·éÆA³Ìf[^Ì嫳âPÊðCɹ¸ÉÏÞBW»³ê½c·ÍAW{ÉîÃc·ÌWηðßAec·ð»ÌWηÅéB
![]() @±ÌWc·Ìlª}3.0ðz¦Ä¢êÎu͸êlvÌÂ\«ª éB
@±ÌWc·Ìlª}3.0ðz¦Ä¢êÎu͸êlvÌÂ\«ª éB
(2-6)@PñA®ðgpµÄA¢mÌlð\ª·éB
à¾ÏÊ(ê)ÌlÍí©ÁÄ¢éªAÚIÏÊ(w)Ì_ªs¾ÈAß½PñA®ðgpµÄAlð\ª·éB±Ìæ¤Éß½PñA®ðgpµÄ¢mÌlð\ª·éÍAgpµ½à¾ÏÊÌÍÍàÅ\ª·éª]ܵ¢Bgpµ½à¾ÏÊ©çå«Oê½ÍÍÅ\ª·éÆAë·ªå«ÈèÀpÉK³ÈÈéB
à¾ÏÊÅ éêÌ_Í10Èã90ȺŠéB»±Å±ÌÍÍàÅÌêÌ_ðgpæ¤É·éB¢Üê̱¾¯ó¯½à̪3¼¢½Æ·éB»Ì_ÍA25A68A72A80_Å Á½B±Ì4¼ÌwÌ_ͽ_Æ\z³êé©BPñA®ðgpµÄ\ª·éB
ß½PñA®:Y=0.741379x+15.17241@x̪ÍêÌ_Å é©çA±±ÉêÌ_ð¢êÄlðvZ·éB
ºÌ\Ìæ¤É\ªlð¾é±ÆªÅ«éB
|
|
ê |
ü͵½® |
vZÊ |
|
11 |
25 |
=0.74137931*B15+15.17241379 |
33.7068966 |
|
12 |
68 |
=0.74137931*B16+15.17241379 |
65.5862069 |
|
13 |
72 |
=0.74137931*B17+15.17241379 |
68.5517241 |
|
14 |
80 |
=0.74137931*B18+15.17241379 |
74.4827586 |
15.3.3@ñAÉÖ·éÖ
ªÍc[ðgpµÈÄàAñAÉÖ·éÖðgp·êÎñA¼üÆ\ªlðßé±ÆªÅ«éB
(1)PñA¼üÉÖ·éÖ
@PñA¼üÌX«ðßéÖ(ÏÊXÌWj
@@@=slope(ÚIÏÊÌÍÍ,à¾ÏÊÌÍÍ)
APñA¼üÌYØÐðßéÖ
@@@=intercept(ÚIÏÊÌÍÍ,à¾ÏÊÌÍÍ)
BêxÉPñA¼üÌX«ÆYØÐðßéÖ
@@@=linest(ÚIÏÊÌÍÍ,à¾ÏÊÌÍÍ,[è],[â³])
èÍwèµÈÄàæ¢Bâ³Ítrue,falseÌ¢¸ê©ðwèAȪ·éÆfalseÆÝȳêéBtrueðwè·éÆAñAÉÖ·éªÍîñª\¦³êé½¾µlinestÖÅÍAzñ®ð쬵ȯêÎ\¦³êÈ¢BB
(2)ÖWÉÖ·éÖ
@2ÏÊÔÌÖWðßéÖ
@@@=correl(ÏÊ1ÍÍ,ÏÊ2ÍÍ)
AèWiR2)ðßéÖ
@@@=rsq(ÚIÏÊÌÍÍ,à¾ÏÊÌÍÍ)
(3)PñA®ðgpµÄ\ªlðßéÖ
@\ªlðßéÖ
@@@=trend(ÚIÏÊÌÍÍ,à¾ÏÊÌÍÍ,è)
@@@=forecast(è,ÚIÏÊÌÍÍ,à¾ÏÊÌÍÍ)
(2)ÖðgpµÄAPñA®ðßéB
PñA®ÍAY=b1x+b0
ÚIÏÊ(wÌ_)ÌÍÍ:C3:C12Aà¾ÏÊ(êÌ_)ÍÍ:B3:B12Å éB
X«:=slope(ÚIÏÊÍÍ,à¾ÏÊÍÍ)©ç0.74137931ÆßçêéB
YØÐ:=intercept(ÚIÏÊÍÍ,à¾ÏÊÍÍ)©ç15.1724438ÆßçêéB
æÁÄAPñA®ÍAY=0.74137931X+15.1724438ÆßçêéB
dÖW:=rsq(ÚIÏÊÍÍ,à¾ÏÊÍÍ)æè0.68277972
ÖWÍ2ÏÊX¥YÌÖÅ é©ç=correl(ÏÊ1ÍÍ,ÏÊ2ÍÍ)æè0.82630486

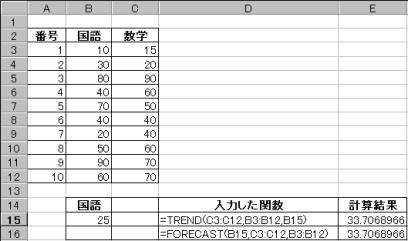
(3)à¾ÏÊ(êÌ_)ª25_ÌÌÚIÏÊ(wÌ_)ðÖÅßéB
êÌ_)(25)Z:B15@
=trend(ÚIÏÊÍÍ,à¾ÏÊÍÍ,êÌ_)æèwÌ_Í33.7068966_Æ\ª
=forecast(êÌ_,ÚIÏÊÍÍ,à¾ÏÊÍÍ)æèwÌ_Í33.7068966_Æ\ª
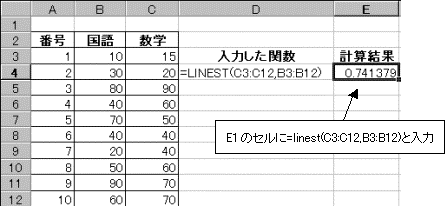
(3)PñA¼üÌX«ÆYØÐðêxÌßéÖÌgp
vZÊƵÄAuX«vÆuYØÐvÌ2ÂÌlª~µ¢B»Ì¼ÌªÍÊà\¦³¹éB
@=linest(ÚIÏÊÍÍ,à¾ÏÊÍÍ,,true)Åܸ¼üÌX«ðßéB
@@@¦trueðȪ·éÆAeÏÊÌWÆYØÐl¾¯Ì\¦ÆÈéB
Azñ®ð쬷éB
ß½¢ÏÍ2ÂA¢Ü1ÂßÌX«ªßçêÄ¢éÌÅA¼Ì1Âðzñ®Å\¦³¹éB
Öðü͵½Êu©çE¤É1ZªhbOµAXɺûüÉ5sªÍÍwè·é(ß½¢lª2 é)¨®o[ðNbNµÄANeBuÉ·é¨CTRLL[+SHIFTL[+ENTERL[ð·ÆA2ÔÚÉl:YØÐâ»Ì¼ÌªÍʪ\¦³êéB
![]()
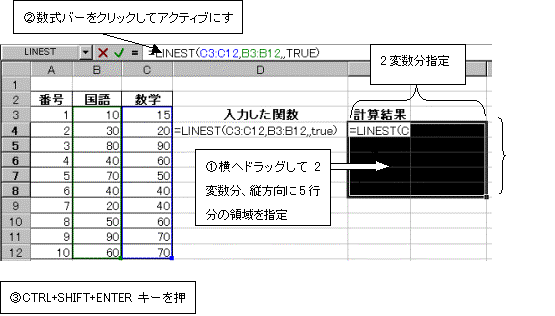
BlinestÖÌvZÊðmF
linestÖðgpµAzñ®É·éƺÌæ¤ÈvZʪ\¦³êéB
|
|
YØÐ |
|
X1ÌWë· |
YØÐÌWë· |
|
èW |
Wë· |
|
ªUä |
©Rx |
|
ñA̽ûa |
c·Ì½ûa |
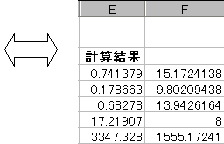
±ê©çAX«:0.741379@YØÐ:15.1724138@
æÁÄPñA®:Y=0.741379X+15.1724438ÆßçêéB
ܽ±ÌPñA®ÌM«ÍªUä(F):17.21907@©Rx1A8ÌFªzð²×êÎæ¢BiPñAÅÍ1ÔÚÌ©RxÍ1)
ñA̽ûaÍ3347.328@©Rx:1@c·Ì½ûa:1555.17241@©Rx:8
VR=3347.328@VE=1555.172418=194.39655@![]() @ÆßçêéB
@ÆßçêéB
=finv(0.05,1,8)=5.317645©ç©Rx1,8Ìã¤0.05m¦ÌFlðär·êÎæ¢B
èvÊ(F)=17.219F1,8(0.05)=5.317645@Å é©ç@VRàVEÆ¢¤A³¼àðüpÅ«éB
16.@dñAªÍ
PñAªÍÅÍAÚIÏÊÍ1Âà¾ÏÊà1ÂÅ Á½BÚIÏÊÍíÉ1Â(\ª·élÍ1Â)Å éªAà¾Ïʪ2ÂÈãÌðdñAªÍÆ¢¤BPñAÉä׸xÍãªéªAÀ±ãÅÍA³ÊÈÏÊðgÁĢȢ©è·éKvª èA³ÊÈÏÊðgí¸(ÏÊIð@)ÅÇÌdñA®ð¾éKvª éB
16.1@dñA®ðßé
êÊÉà¾Ïʪp éÌdñAfÍ@yi=À1¥x1i+À2¥x2i+c+Àp¥xpi+À0+Ãi@(i=1,2A@cn)Å\³êéB±ÌPñA®ð¯lÉ
c·(Ã)É¢Ä
@ÃiÆÃjͨݢÉƧŠèA³KªzN(0,Â2)É]¤B
AÃiÌúÒl(½Ïl)Í0Å èAܽªUÍêèÅ éB
̼èºÅAdñA®ðYi=b1¥x1i+b2¥x2i+c+bp¥xpi+b0Æ·éÆAb0,,b1cbpÍÀ0,À1cÀpÌèÊÅ éB
b0,,b1cbpðÎñAWÆÄÑAÀ0,À1cÀpðêÎñAWÆ¢¤BPñA®Æ¯lÉc·½ûa°(Ãi)2ðŬɷéæ¤ÈAb0,,b1cbpðßêÎæ¢B

16.2@dñAªÍðÀ{
16.2.1@ªÍc[ðgpµÄdñAªÍÀ{
@ éX[p[ÅAxX8XÜÉ¢ÄèêÌ\¬xEXõ̳çxE¤iÌ]xÆXÜ1u ½èÌã𲸵½Æ±ëAºÌæ¤Èʪ¾çê½BãðÚIÏÊƵAèê\¬xEXõ³çxE¤i[Àxðà¾ÏÊƵÄdñAªÍðÀ{·éB
èê\¬x:7@Xõ³çx:5@¤i[Àx:5@ÌXÜðVKÉJX·éÆ·éÆèã°Í1u ½è¢çÆ\ª³êé©B
(1)ªÍ·éf[^ðüÍ·éB
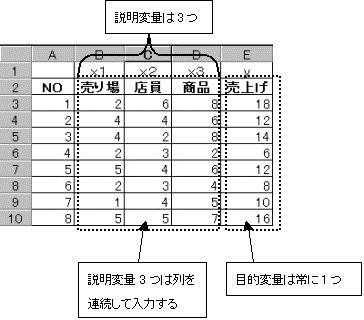
¦à¾ÏÊðüÍ·éÍAsܽÍñûüÉA±µ½ÍÍÉüÍ·éB
(2)c[¨ªÍc[ñAðIð·éB
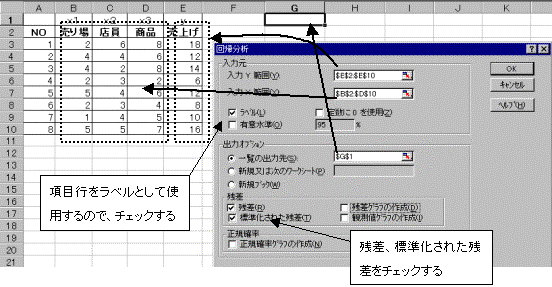
üÍÍÍ(Y)ÍÚIÏÊÌÍÍÅ éBüÍÍÍ(X)Íà¾ÏÊÌÍÍÅ éB±±ÅÍà¾Ïʪ3ñA±µÄ éÌÅAà¾ÏÊÌÍÍð·×Äwè·éBȨAæªs̶ðxƵÄwè·ÌÅAxðNbNµÄIðµµÄ¨Bc·EW»³ê½c·ÌàNbNµÄ`FbNµÄ¨BSÄÌÝèªI¹µ½çAOK{^ðNbNµÄªÍðJn·éB
(3)ªÍÊð¢
(3-1)dÖWÖW
|
ñAv |
|
|
dÖ R |
0.98651286 |
|
dè R2 |
0.97320763 |
|
â³ R2 |
0.95311334 |
|
Wë· |
0.86613306 |
|
Ϫ |
8 |
dÖW(R):0.98651286cÚIÏÊÆñA®æèß½\ªlÌÖÍ©È袱ƪí©éB
dèW(R2):0.97320763cñAÏ®Ì䦪©ÈèAdñA®ÍM«ª éÆvíêéB
(3-2)ß½dñA®ÌM«ðªUªÍ\ÅmF
|
ªUªÍ\ |
|
|
|
|
|
|
|
©Rx |
Ï® |
ªU |
Ϫ³ê½ªUä |
LÓ F |
|
ñA |
3 |
108.9993 |
36.33308 |
48.43207 |
0.001334 |
|
c· |
4 |
3.000746 |
0.750186 |
|
|
|
v |
7 |
112 |
|
|
|
Ϫ³ê½ªUä(F)Í©Rx3,4ÌFªzÉ]¤B¢ÜªUä(F):48.43207Å èA»Ìm¦l:0.001334Å éB
èðÀ{
@¼àð½Äé
A³¼à@ñA¼üÍ\ªÉð§½È¢(VRàVE)
Χ¼à@ñA¼üÍ\ªÉð§Â@@(VRVE)
AèvÊðßé
@@@èvÊ(F)=48.43207ÍA©Rx3,4ÌFªzÉ]¤B
BL×m¦5%ÅãФèðÀ{
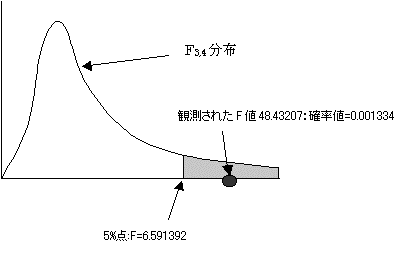
ȨAF3,4(0.05)ð²×éÆA6.591392Å éB=fdist(0.052,3,4)ÅßçêéB
Ϫl(F):48.43207F3,4(0.05):6.591392Å èA±ÌÌm¦l:0.001334Í0.05æèଳ¢BæÁÄüpæÉüéBA³¼àðüp·éBñA®Í\ªÉð§ÂÆ¢¦éB
(3-3)ÎñA®ÌM«ðmF
|
|
W |
Wë· |
t |
P-l |
ºÀ 95% |
ãÀ 95% |
ºÀ 95.0% |
ãÀ 95.0% |
|
ØÐ |
-1.3788229 |
1.279866 |
-1.07732 |
0.341975 |
-4.93231 |
2.174662 |
-4.93231 |
2.174662 |
|
èê |
0.11984513 |
0.242232 |
0.494754 |
0.646716 |
-0.5527 |
0.792389 |
-0.5527 |
0.792389 |
|
Xõ |
1.06212482 |
0.289351 |
3.670711 |
0.021378 |
0.258755 |
1.865494 |
0.258755 |
1.865494 |
|
¤i |
1.54583881 |
0.197781 |
7.815898 |
0.001446 |
0.996709 |
2.094969 |
0.996709 |
2.094969 |
eÎñAWæYØÐlÍX1:0.11984513@X2:1.06212482@X3:1.54583881@YØÐ:-1.3788229
æÁÄßçê½dñA®ÍY=0.11984513X1+1.06212482X2+1.54583881X3-1.3788229
Éeà¾ÏÊÌM«ð¢·éB
@èê(X1ÏÊ)
tl:0.494754@±ÌÌm¦:0.646716D±êÍuA³¼à:à¾ÏÊX1Í\ªÉð§½È¢vðüpÅ«È¢BæÁÄÏÊX1Æ\ªÉð§ÂÆÍ¢¦È¢B
AXõ(X2ÏÊ)
tl:3.670711@±ÌÌm¦:0.021378±êÍuA³¼à:à¾ÏÊX2Í\ªÉð§½È¢vðüp·éBæÁÄÏÊX2Í\ªÉð§ÂÆ¢¦éB
B¤i(X3ÏÊ)
tl:7.815898@±ÌÌm¦:0.001446±êÍuA³¼à:à¾ÏÊX3Í\ªÉð§½È¢vðüp·éBæÁÄÏÊX3Í\ªÉð§ÂÆ¢¦éB
CYØÐ
tl:-1.07732@±ÌÌm¦:0.341975±êÍuA³¼à:YØÐÍ\ªÉð§½È¢vðüpÅ«È¢BæÁÄYØÐÍ\ªÉð§ÂÆÍ¢¦È¢B
Èã©çßçê½dñA®Í\ªÉð§ÂÆ¢¦éªAÏÊX1(èêÌ\¬x)ÆYØÐÍ\ªÉð§ÂÆÍ¢¦È¢B
(3-4)\ªlÆc·ð¢
ªÍ·éf[^ÆAdñA®ðgpµ½\ªlÌ\ðí¹ÄÝéƺÌæ¤È\ÉÈéB
Àãf[^ÆAñA®©ç¾çê½f[^Ì·ªc·Å èAc·àvZ³êÄ\¦³êÄ¢éB
|
|
P |
Q |
R |
|
|
||
|
NO |
èê |
Xõ |
¤i |
ã° |
\ªl: ã° |
c· |
Wc· |
|
1 |
2 |
6 |
8 |
18 |
17.6003268 |
0.3996732 |
0.6104350 |
|
2 |
4 |
4 |
6 |
12 |
12.6240898 |
-0.6240898 |
-0.9531944 |
|
3 |
4 |
2 |
8 |
14 |
13.5915178 |
0.4084822 |
0.6238893 |
|
4 |
2 |
3 |
2 |
6 |
5.1389195 |
0.8610805 |
1.3151587 |
|
5 |
5 |
4 |
6 |
12 |
12.7439349 |
-0.7439349 |
-1.1362381 |
|
6 |
2 |
3 |
4 |
8 |
8.2305971 |
-0.2305971 |
-0.3521991 |
|
7 |
1 |
4 |
5 |
10 |
10.7187156 |
-0.7187156 |
-1.0977197 |
|
8 |
5 |
5 |
7 |
16 |
15.3518986 |
0.6481014 |
0.9898683 |
èê\¬x(ÏÊX1):7@Xõ³çx(ÏÊX2):5@¤i[Àx(ÏÊX3):5@ÌãÍ¢çÆ\ª³êé©Aß½dñA®ðgpµÄvZµÄßéB
ßçê½dñA®:Y=0.11984513X1+1.06212482X2+1.54583881X3-1.3788229
±Ì®ÉX1¥X2¥X3ÌÏÊÌlðüÍ·éÆAY=12.4999à12.5ÆßçêéB
1u ½è12.5ÌãÆÈéÅ ë¤B
16.2.2@dñAÉÖ·éÖðgpµÄdñAªÍðÀ{
PñAªÍÌÍAÚIÏÊÍPÂAà¾ÏÊà1ÂÅ Á½Bµ©µdñAªÍÌÍAÚIÏÊÍ1ÂÅ éªAà¾ÏÊÍ2ÂÈãÆÈéBdñA®ðßéÉÍAgpµÄ¢éà¾ÏʲÆÌWÆYØЪKvÆÈéB
(1)eÏÊÌWÆYØÐAdñA®ÌèðÀ{·éÖFlinestÖgp
=linestÖ:=linest(ÚIÏÊÍÍ,à¾ÏÊÍÍ,,true)
@ܸ=linestÖÅA¤i(à¾ÏÊX3)ÌWðßéB
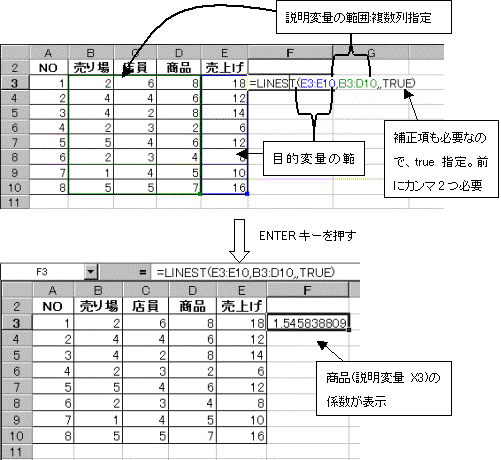
A檪ÜÁ½çAzñ®ðwè
¢ÜgpµÄ¢éà¾ÏÊÍ3ÂAæÁÄWÍà¾Ïʪ3ÂÆYØЪ1ÂÌv4ÂÌWªKvÅ é©çAzñwèÍ¡ûüÉ4ñªKvBܽcûüÉÍAíÉ5sªÌÍͪKvBæÁÄzñwèÌÍÍÍA¡Ö4ñEcÖ5sªwè·éBÉ®o[ðNbNµANeBuɵ½ãACTRLL[+SHIFTL[+ENTERL[ðµÄzñ®ð®¬·éB
|
X3W |
X2W |
X1W |
YØÐ |
|
1.5458388 |
1.0621248 |
0.11984 |
-1.378822 |
|
|
X2Wë· |
X1Wë· |
X4Wë· |
|
0.1977813 |
0.2893512 |
0.24223 |
1.2798659 |
|
èW |
Wë· |
|
|
|
0.9732076 |
0.8661330 |
#N/A |
#N/A |
|
ªUä |
c·©Rx |
|
|
|
48.432070 |
4 |
#N/A |
#N/A |
|
ñA½ûa |
c·½ûa |
|
|
|
108.99925 |
3.0007459 |
#N/A |
#N/A |
CÖÅßçê½elðAñAªÍpÉðß·éB
1sÚÉÍAeà¾ÏÊÌWªX3¥X2¥X1¥YØÐÌÉ\¦³êéB±ê©çßédñA®:Y=0.11984513X1+1.06212482X2+1.54583881X3-1.3788229@ªßçêéB
èW(R2):0.9732076
ªUä(F):48.432070@ªUä(F)Ì©RxÍ2 èAvZÊÍ2ÔÚÌc·Ì©Rxª\¦³êÄ¢éB1ÔÚÌ©RxÍAñAÏ®(SR)Ì©RxÅ èAà¾ÏÊÌÂ(p)Å éB¢ÜÍ3ÂgpµÄ¢éÌÅA1ÔÚÌ©RxÍ3Å éB2ÔÚÌ©RxÍAc·Ï®(SE)Ì©RxÅ èAW{(n)-à¾ÏÊÂ(p)-1Å éB±êÍ4ÆvZ³êÄ\¦³êÄ¢éBÈã©çϪ³ê½ªUä(F)Í©Rx3,4ÌFªzÉ]¤B³çÉÖðgpµÄF3,4(0.05)ðßêÎAã¤5%_ÌFlªí©éÌÅA±ÌlÆϪ³ê½ªUä(F)ðär·êÎæ¢BF3,4(0.05)ÍÖÅÍA=finv(0.05,3,4)Å èA±ÌlÍ6.591392321Æ\¦³êéBܽªUä(F):48.432070@©Rx3,4Ìm¦lÍA=fdist(48.43207,3,4)©ç0.001334ÆßçêéBÈãðÜÆßÅ}\\¦·éƺÌæ¤ÈOtÆÈéB±êͪÍc[Åß½lƯ¶ÉÈéB
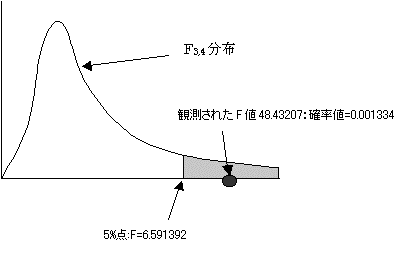
üpæÉüéÌÅAñAÏ®ÍøʪȢðüp·éBñAÏ®Íøʪ éBß½ñA®Í\ªÉð§ÂÆ¢¦éB
(2)trendÖÅ\ªlðßéB
trendÖðgp·êÎAdñA®ð©®IÉßÄA»ÌdñA®Éæé\ªlðÊƵÄ\¦µÄêéB
trendÖ:=trend(ÚIÏÊÍÍ,à¾ÏÊÍÍ,è)Å éªA±±ÅÚIÏÊÍÍÍwèãf¥4L[ðµÄAâÎÀWÉ·éBܽà¾ÏÊÌÍÍwèã¯lÉf¥4L[ÅâÎÀ\¦·éBèÌÍÍÍAà¾ÏÊÌX1¥X2¥X3Ìæªsðwè·êÎæ¢B±Ìæ¤ÉµÄ¨¯ÎA»ÌÜܺûüÉü©ÁÄRs[·éÆ·×ÄÌ\ªlª·®ÉßçêéB


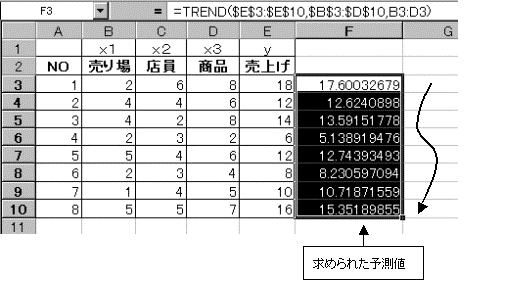
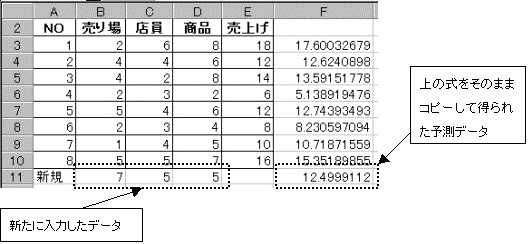 èê\¬x:7@Xõ³çx:5@¤i[Àx:5@ÌÌ1u ½èÌãð\ª·éÉÍAà¾ÏÊf[^̺Ìó¢Ä¢ésÉf[^ðX1¥X2¥X3ÌÉü͵AãÌ®ð±¯Ä»ÌÜܺÉRs[·êÎæ¢Bßçê½ÊÍ12.999112Å èAªÍc[Åß½ÊƯ¶lð¾é±ÆªÅ«éB
èê\¬x:7@Xõ³çx:5@¤i[Àx:5@ÌÌ1u ½èÌãð\ª·éÉÍAà¾ÏÊf[^̺Ìó¢Ä¢ésÉf[^ðX1¥X2¥X3ÌÉü͵AãÌ®ð±¯Ä»ÌÜܺÉRs[·êÎæ¢Bßçê½ÊÍ12.999112Å èAªÍc[Åß½ÊƯ¶lð¾é±ÆªÅ«éB
16.2.3@dñAªÍ̽d¤ü«
à¾ÏÊÔŨݢɢ֪ èAÉÍÎñAWðßé±ÆªÅ«È¢Æ¢¤»Ûðø«N±·±Æª éB±êð½d¤ü«Æ¢¤Bà¾ÏÊÔŨݢɢ֪ éÆ¢¤±ÆÍAÇ¿ç௶±ÆðྵĢéÏÈÌÅAÇ¿ç©êûÌÏʪ êÎ[ªÅ éÆ¢¦éBdñA®ðßéÉ ½èA½d¤ü«ª éÉÍÇ¿ç©Ìà¾ÏÊðƵÄßéKvª éB
(1)½d¤ü«ÌL³
½d¤ü«ª é©Ç¤©ÍºÌæ¤Èvöð²×êÎæ¢B
@à¾ÏÊÔÌPÖWðßAPÖWª1ܽÍ|1Éߢà̪ êνd¤ü«ªFßçêéB
A½d¤ü«ªFßçêéÉÍAÏñAWðßçêȢƩAÏñAWÌÆà¾ÏÊ¥ÚIÏÊÔÌPÖWªêvµÈ¢Æ¢¤»ÛðN±·B
(2)½d¤ü«Ìá
à¾ÏÊX1`X3ÆÚIÏÊYªºÌæ¤É éÆ·éB
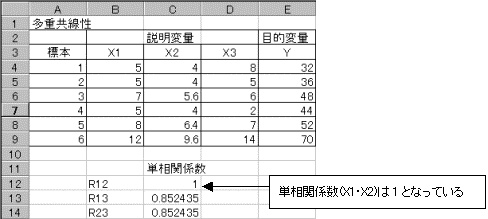 à¾ÏÊ(X1`X3)Ì2ÏÊÔÌPÈÖWðuPÖWvÆ¢¤B±ÌPÖWðà¾ÏÊÔŲ×éBPÖW(X1¥X2):1@PÖW(X1¥X3):0.852435@PÖW(X2¥X3):0.852435@ÆÈÁÄ¢éBPÖW(X1¥X2)Í1ÆÈÁÄ¢éB±Ì±ÆÍAà¾ÏÊX1Æà¾ÏÊX2ͯ¶ðྵĢéÌÅAÇ¿ç©êûÌÏÊðgp·êÎA¼ûÌÏÊÍsvÈÏÊÅ éBÇ¿ç©ÌÏÊðƵÄAdñAªÍð·éKvª éB
à¾ÏÊ(X1`X3)Ì2ÏÊÔÌPÈÖWðuPÖWvÆ¢¤B±ÌPÖWðà¾ÏÊÔŲ×éBPÖW(X1¥X2):1@PÖW(X1¥X3):0.852435@PÖW(X2¥X3):0.852435@ÆÈÁÄ¢éBPÖW(X1¥X2)Í1ÆÈÁÄ¢éB±Ì±ÆÍAà¾ÏÊX1Æà¾ÏÊX2ͯ¶ðྵĢéÌÅAÇ¿ç©êûÌÏÊðgp·êÎA¼ûÌÏÊÍsvÈÏÊÅ éBÇ¿ç©ÌÏÊðƵÄAdñAªÍð·éKvª éB
à¾ÏÊX2Íà¾ÏÊX1Ì0.8{ÆÈÁÄ¢éB±êÍÜÁ½¯¶ðྵĢé±ÆÉÈéB
¦PÖWÍA ÜÅàPÈ2ÏÊÔÌÖW̱ÆÅ éBdñAªÍÅÍAgpµÄ¢éà¾ÏÊ̪2ÂÈãÆÈé½ßÉA¨Ý¢Ée¿µ¤ÌÅAPÖWª2ÏÊÔÌÖWð\·ÆÍÀçÈ¢B½ÏÊÅ2ÏÊÔ̳mÈÖWðßéÉÍAÎÖWðßéKvª éB
16.2.4@WÎñAW
à¾ÏʪÇêç¢ÚIÏÊÉe¿ð^¦Ä¢é©(ñ^µÄ¢é©)ð²×éÉÍAß½dñA®ÌÎñAWð©êÎæ¢BÎñAWªå«¢ÙÇÚIÏÊÉ^¦ée¿ªå«¢Æ¢¦éBµ©µAà¾ÏÊÔÅPʪÙÈéÉÍAPÊÌe¿ðó¯éÌÅAPÉÎñAWÌå¬ðßé±ÆÍÅ«È¢BPÊÌe¿ðæèÉÍAf[^ðW»·êÎæ¢Bf[^ðW»·é±ÆÉæèA½Ï=0@ªU=1ÆÈèPÊÌe¿ðó¯ÈÈéÌÅAW»µ½f[^©çÎñAWðßéæ¤É·éB±Ìæ¤ÉW»µ½f[^©çß½ÎñAWðuWÎñAWvÆ¢¤BWÎñAWªå«¢ÙÇAÚIÏÊÉ^¦ée¿ªå«Añ^Ìå«¢ÏÊÆ¢¦éB

æÌáèÌf[^ðW»·éƺÌæ¤È\ÉÈéB
±ÌáÅÍAà¾ÏÊÌPʪ¯¶Å é©çAßçê½ÎñAWðär·é¾¯Å梪AW»µÄmFµÄÝéB
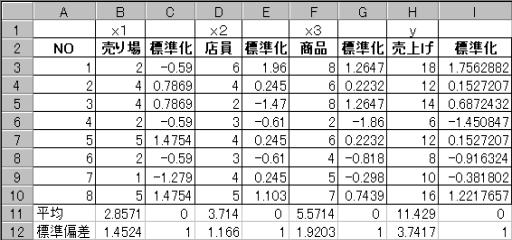
W»µ½f[^Ìݲ«oµµÄAVµ¢\ð쬷é

±ÌW»³ê½ef[^ðgpµÄAdñAªÍ·éÆAeÎñAWÍAãÌæ¤È\ÆÈéB±ÌW»³ê½ÎñAWð©éÆA¤iÌÎñAWªêÔå«AÉXõÌÎñAWÆÈÁÄ¢éBà¾ÏÊX3(¤i)ÌÚIÏÊ(ã°)^¦ée¿ªêÔå«¢B
ܽ®ðgpµÄAW»µ½ÎñAWðßÄ௶Êð¾çêé
W»OÌÏÊX1:0.119845132@X1ÌWηYÌWη=0.3881619@
W»µ½ÌÏÊX1ÌW:0.119845132~0.3881619=0.046519
¼Ìà¾ÏÊÉ¢ÄsÁÄà¯lÌÊÆÈéB