6.�@��{���v�ʂ����߂�
6.1�@��{���v��
�@��W�c���疳��ׂɕW�{�𒊏o����B���̒��o���ꂽ�W�{�ɂ��āA��{���v�ʂ����߃f�[�^�̓��������ށB��{���v�ʂƂ��ẮA�W�{���A���v�A���ρA�����l�A�ŕp�l�A�ő�A�ŏ��A�͈́A���U�A�W�����A�W���덷�A�c�x�A��x�Ȃǂ�����B
�@
|
��{���v�� |
�Ӂ@�@�� |
�Ή��������� |
|
�W�{�� |
��W�c���璊�o�����W�{�̌��@ |
=COUNT(�͈́j |
|
���v |
���v�l |
=SUM(�͈�) |
|
���� |
���v���� |
=AVERAGE(�͈�) |
|
�����l ���f�B�A�� |
�W�{�f�[�^�����������ɕ��ׂ����ɒ����ɂ���l�i�f�[�^�������̎��́A����2�̕��ϒl�j |
=MEDIAN(�͈�) |
|
�ŕp�l:���[�h |
�ł������o������l |
=MODE(�͈�) |
|
�ő� |
�ő�̒l |
=MAX(�͈�) |
|
�ŏ� |
�ŏ��̒l |
=MIN(�͈�) |
|
�͈� |
�f�[�^�͈̔́F�ő�-�ŏ� |
=MAX(�͈�)-MIN(�͈�) |
|
���U |
�f�[�^�̕��U�̒��x |
=VAR(�͈�) |
|
�W���� |
���U�̕����� |
=STDEV(�͈�) |
|
�W���덷 |
�W������(�W�{���̕�����) |
=STDEV((�͈́j/COUNT(�͈�)^(1/2) |
|
�c�x |
�O���t�̘c�ȋ�B0�ɋ߂��قǐ��K���z�ɋ߂� |
=SKEW(�͈�) |
|
��x |
�O���t�̐���B3�ɋ߂��قǐ��K���z�ɋ߂� |
=KURT(�͈�) |
6.2�@��{���v�ʂ����߂�
��{���v�ʂ����߂�ɂ́A�@�蓮�Ōv�Z�����쐬���ċ��߂�A�����g�p���ċ��߂�B��{���v�ʌv�Z�c�[�����g�p���Ĉ�x�ɋ��߂�B�ȏ�3�̕��@������B�ʏ�1�����߂�ɂ́A�����g�p���A���v�v�Z�Ƃ��Ĉ�x�ɑS�̂����������ɂ̓c�[�����g�p����B
6.2.1�@��{���v�ʂ������g�p�����߂�
�@����14�l�̊w�����������A���̌��ʂ��ȉ��̂悤�ȃf�[�^�ł������Ƃ���B
|
No |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
�_ |
45 |
66 |
53 |
45 |
72 |
51 |
46 |
32 |
46 |
62 |
51 |
65 |
51 |
58 |
�_���͐��K���z�ɏ]�����̂Ƃ���B�ʏ�W�{���͂�����x�̑傫����K�v�Ƃ��邪�A���ܕW�{����14���Ə��Ȃ����A����14���̕W�{�ɑ��Ċ����g�p���Ċ�{���v�ʂ����߂�B
(1)�W�{�f�[�^����͂���B1��܂���1�s�ɘA�������͈͂œ��͂���B
(2)���E�B�U�[�h���g�p���āA���v�̊����w�肷��B���Ŏg�p����͈͂̓h���b�O���Ďw�肷��B
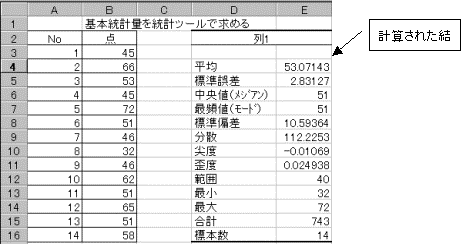
(3)�v�Z���ʂ��\�������B

6.2.2�@���v�c�[�����g�p���āA��{���v�ʂ����߂�B
(1)���͂���f�[�^����͂���B
(2)�c�[�������̓c�[����I���B�f�[�^���̓{�b�N�X���J������{���v�ʂ�I����OK�{�^�����N���b�N
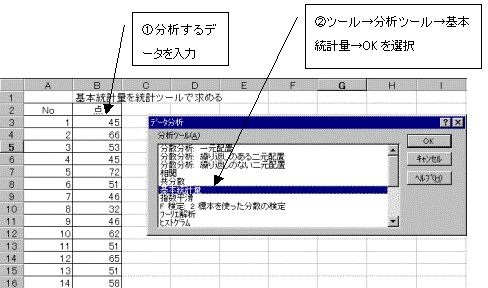
(3)���͔͈͂��w�肷��B���͂���f�[�^�����͂���Ă���͈́B�����ł�B3����B16�B
���ɏo�͐���w�肷��B�v�Z���ʂ�\������擪�̃Z���ʒu���w��B�����ł�D2�B
�o�̓I�v�V�����͓��v�����N���b�N���w��B�Ō��OK�{�^�����N���b�N�B
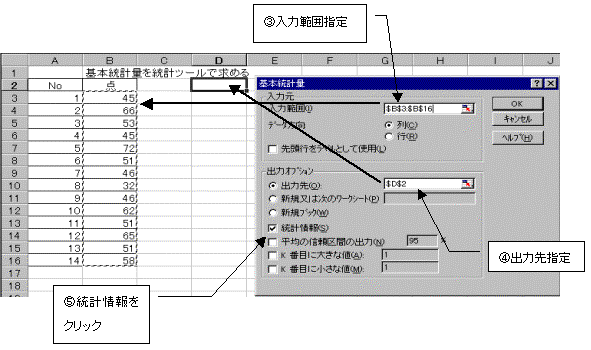
(4)�o�͐�Ɋ�{���v�ʂ��v�Z����ĕ\�������B
�v�Z���ʂ��\�������̂ŁA�f�[�^�̈ꕔ�����Ƃ���ύX�������ɂ́A�ēx���̓c�[���Ŋ�{���v�ʂ��v�Z�������Ȃ���Ȃ�Ȃ��B���ŋ��߂����ɂ́A�f�[�^�̈ꕔ���ォ��ύX���Ă��Čv�Z����Ď����I�ɐV�����l�\���ƂȂ�B
6.2.3�@�e��{���v�ʂ̈Ӗ�
(1)���U
���U�ɂ́A�W�{���U�ƕꕪ�U(��W�c�̕��U)�Ƃ�����B���U�́A���ϒl����e�f�[�^���ǂꂭ�炢�U����Ă��邩�����邽�߂̂��̂ł���B�P���ɂ��ׂẴf�[�^�ɂ���(���ϒl-�e�f�[�^�l�j�����߁A�����Ă�����0�ɂȂ��Ă��܂��B�����ŁA���ׂẴf�[�^�ɂ��āi���ϒl-�e�f�[�^)�Q�����߁i�������Ƃ����j�A����𑫂��Ă����悤�ɂ���B���i���ϒl-�e�f�[�^)�Q(�������a�Ƃ���)�B���̕������a��(�W�{��-1)�Ŋ��������̂��A�W�{���U�ł���B

���ʏ�A�W�{����������x�傫���Ȃ�A�W�{���U�ƕꕪ�U�͂قړ����l�ƂȂ�B
(2)�W����
���U�͕��ς���̂��������đ����Ă��������̂ł���B���̂��������邽�߂ɕ��U�̕��������Ƃ��Č��ɖ߂������̂��A�W�����ł���B
�@�@�@�W����=![]()
�W���������U�Ɠ��l�ɁA�W�{�W�����ƕ�W����������B�Ⴂ�́A�W�{�W�����́A�W�{���Ƃ���N-1���g�p���邪�A��W�����͕W�{��N���g�p����B����͕��U�Ɠ����ł���B
���ł́A�W�{�W�����F=stdeva(�f�[�^�͈�)�@��W�����F=stdev(�f�[�^�͈�)�ł���B
(3)�W���덷�iSE�j
�W�������e�f�[�^�̂������������v�ʂł��邪�A�W���덷�́A�W�{���ς̂������������v�ʂł���B![]() �ŋ��߂���B
�ŋ��߂���B
(4)��x
��x�̓O���t�̐���𐔒l���������̂ł���B��x(a)��3��菬�����Ɗ��炩�ȋȐ��ƂȂ�A3�ɋ߂��Ɛ��K���z�ɋߎ����A3���傫���l�ƂȂ�Ɛ�����Ȑ��ƂȂ�B

�@a<3�@������ア�@�@�@�@�@a��3�@���K���z�ɋ߂��@�@�@�@a>3�@���������
(5)�c�x
�@�c�x�͐��K���z�ɔ�ׂǂꂭ�炢�c�Ȃ��Ă��邩�𐔒l���������̂ł���B�c�x(a)�����̎��ɂ́A�Ȑ��̒��_���E�ɂ���Ă���A0�ɋ߂����ɂ͐��K���z�ɋ߂��A���̎��ɂ͋Ȑ��̒��_�����ɂ���Ă���B

�@a<0�@���_���E�ɂ���Ă���@a��0�@���K���z�ɋ߂��@�@�@�@a>0�@���_�����ɂ���Ă���
7.�@�x�����z�\�E�q�X�g�O�����̍쐬
�W�{���W�߂����A�܂���{���v�ʂ����ߐ��l�f�[�^���炨���悻�̕W�{�̌X���ׂ�B���ɓx�����z�\���쐬���A���l�f�[�^�̕��z�ׁA�q�X�g�O�������쐬���ăO���t�����A�f�[�^�̌X�������o�I�ɕ\������B
7.1�@�c�[�����g�p�����x�����z�\�E�q�X�g�O�����̍쐬
�x�����z�\�Ƃ́A�f�[�^���������̕����������K���ɕ����A���ꂼ��̃f�[�^���ǂ̊K���ɑ����Ă��邩���J�E���g�i�x���j�������̂ł���B�ʏ�K������5�`20�ʂɐݒ肷��B
�x�����z�\���쐬����ɂ́A(�ő�l-�ŏ��l)�����Ԃ����߁A��Ԃ�K���ȕ��i�K�����j�ɂ��A�K����ݒ肷��B�x�����z�\���ł�����A���̓x����_�O���t�ɂ������̂��q�X�g�O�����ł���B
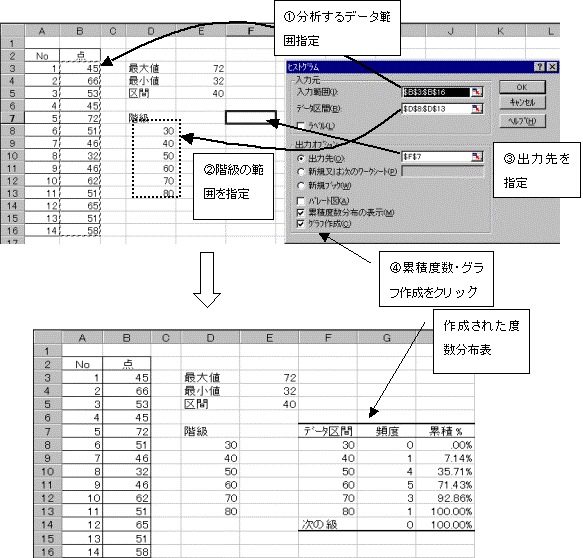
�쐬���ꂽ�q�X�g�O�����c�����ƒ��S�ɍ��E���R�̂悤�ɂȂ��炩�Ɍ������Ă���i���K���z�ɋ߂��O���t�ɂȂ��Ă���j�B
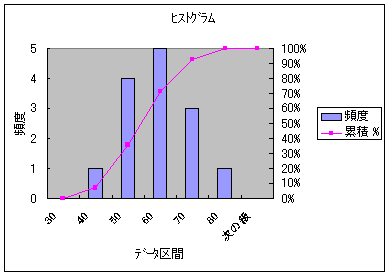
�x�����z�\�ƃq�X�g�O����������A�W�߂��f�[�^�i�W�{�j���炻�̃f�[�^�̂����悻�̕��z��c�����邱�Ƃ��ł���B
7.2�@�f�[�^�̕W����
�f�[�^��W��������ƁA����=0�@���U=1�̕��z�ɕϊ������B�f�[�^��W��������ɂ́A

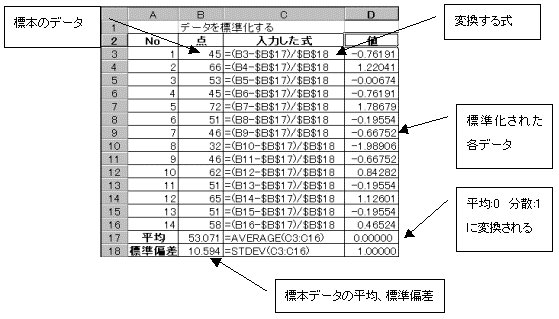
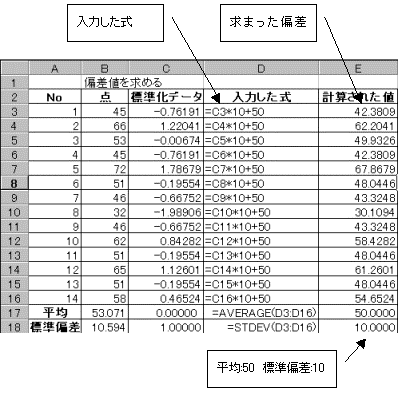
7.3�@���l
�f�[�^��W��������ƁA����=0�@���U=1�@�ɕϊ������B���̕ϊ����ꂽ�f�[�^��=50�@�W����=10�ɂ������̂����l�ł���B
���l=(�W���f�[�^�~10)�{50
�u���W�{�̎���(�W�{��30�ȉ�)�ꕽ�ς̍��̌���v
8.�@�Ή��̂���2�Q�̕ꕽ�ς̍��̌���
�Ή����邩�Ȃ����̈Ⴂ�́A����̌ő̂ɂ��Ẵf�[�^���܂��͈Ⴄ�ő̂ɂ��Ẵf�[�^���̈Ⴂ�ł���B
8.1�@2�Q��W�c���قڐ��K���z�ɏ]�����Ή��̂��鎞�@���@t������{
�������O�̎����̐��тƁA���������̎����̐��тɈႢ���F�߂��邩���댯���i�L�m���j5%�Ō�������{����B2�Q�͂Ƃ��ɐ��K��W�c�ɏ]�����̂Ƃ���B
(1)2�Q�̃f�[�^����͂���B
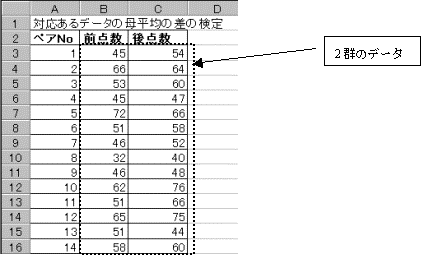
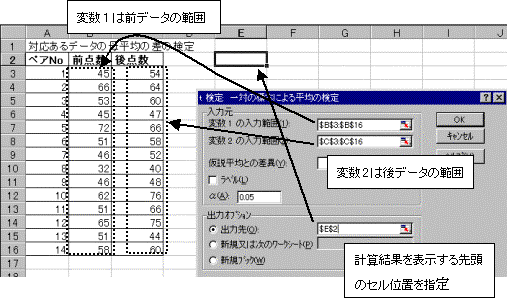
(2)�c�[�������̓c�[����������:1�̕W�{�ɂ�镽�ς̌�����N���b�N
�ϐ�1�̓��͔͈͂́A�O�_���̃f�[�^�͈͂��w��B�ϐ�2�̓��͔͈͂́A��_���̃f�[�^�͈͂��w��B
�o�͐�́A�v�Z���ʂ�\������ʒu�ł���A�擪�̃Z���ʒu���w�肷��B
(3)�v�Z���ʂ�����
OK�{�^�����N���b�N����ƁA�����Ɏw�肵���ʒu�Ɍv�Z���ʂ��\�������B
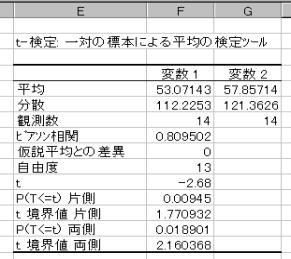
(4)��������{
�@����������
�A�������@H0:���P����2�@�i�Ή�����2�Q�̕ꕽ�ς͓������j
�Η������@H1:���P����2�@�i�Ή�����2�Q�̕ꕽ�ς͓������Ȃ��j
�A���蓝�v�ʂׂ�
���蓝�v�ʁiT�j��t���z�ɏ]���BT=--2.68�@�ʏ�T�l�͐�Βl���g�p����̂ŁA�bT�b=2.68�̐��l���g�p����B
�B�댯���i�L�m���j5���Ō�����s���B��������ł���̂ŏ㑤2.5%�_�ׂ�B
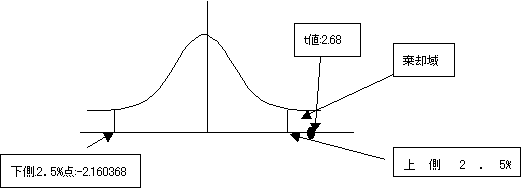
�ϑ����ꂽT�l��2.68�ł���A���p��ɓ���B����āA�A�������͊��p�����B2�Q�̕ꕽ�ςɍ�������Ƃ�����B����O�Ƌ����̕ꕽ�ςɍ�������Ƃ�����B
�܂��AT=2.68�̎��̊m��=0.0189�Ƌ��߂��Ă���A���̒l��0.05�����������̂ŁA���p��ɓ��邱�Ƃ��킩��B
8.2�@���l�Ɋւ����
�@���l�̊m�������߂��
�@�@�@=tdist(t�l�C���R�x�C����)
�@�@�@�@����:1�c�Б��m���@�@����:2�c�����m��
�A�m�����炔�l�����߂��
�@�@�@=tinv(�m���C���R�x)
�B�f�[�^���璼�ڂ���������{�����
�@�@�@=ttest(�ϐ�1�͈́C�ϐ�2�͈́C�����C����̎��)
�@�@�@�@����:1�c�Б�����@����2:��������
![]() �@�@�@�@����̎��:1�c�y�A�W�ɂ���ꕽ�ς̍��̌���
�@�@�@�@����̎��:1�c�y�A�W�ɂ���ꕽ�ς̍��̌���
�@�@�@�@����̎��:2�c�����U�̕ꕽ�ς̍��̌���
�@�@�@�@����̎��:3�c�E�F���`�̌���
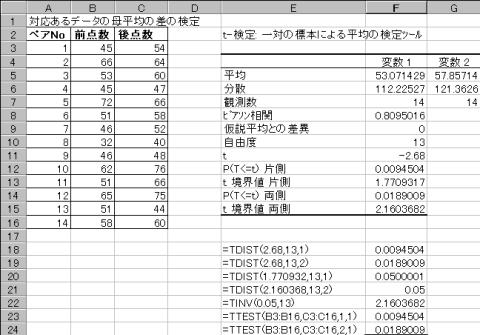
�c�[�����g�p���A����ꂽT�l=-2.68�ł���B���̐�Βl��T=2.68���g�p����B
�uT�l����m�������߂�v
T=2.68�̊m�������߂�B�Б�����ł́@=tdist(2.68�C13�C1)�Ɠ��͂���ƁA0.0094504�ƕ\�������B���̒l��0.05��菬�����̂Ŋ��p��ɓ��邱�Ƃ��킩��B
��������ł�=tdist(2.68�C13�C2�j�Ɠ��͂����0.0189009�ƕ\�������B���̒l��0.025��菬�����̂Ŋ��p��ɓ��邱�Ƃ��킩��B
�u���R�x13��T�l�m��0.05�̂��l�����߂�v
=tinv(0.05�C13)�Ɠ��͂���ƁA2.1603682�ƕ\�������B���̒l�Ƌ��߂�T�l=2.68���r����Ƌ��߂�t�l�̕����傫���̂Ŋ��p��ɓ��邱�Ƃ��킩��B
�u�f�[�^�͈͂��璼�ڑΉ�����2�Q��t����𗼑�����Ŏ��{����v
=ttest(�O�_���͈́C��_���͈́C2�C1)�Ɠ��͂���ƁA0.0189009�Ɗm�����\�������B���̒l��0.025��菬�����̂Ŋ��p��ɓ��邱�Ƃ��킩��B
�c�[�����g�p���Č�������{���Ă��A�����g�p���Č�������{���Ă����ʂ͓����ƂȂ�B
9.�@�Ή��̂Ȃ�2�Q�̕ꕽ�ς̍��̌���
�Ή��̂Ȃ����K��2�W�c�̕ꕽ�ς̍��̌�������{����B
�Ή��̂Ȃ����K��2�W�c�́A�����U�����������
![]() �@�@�@�����U�ł��遨�����U�̎���t��������{
�@�@�@�����U�ł��遨�����U�̎���t��������{
�@�@�@�����U�łȂ��������U�łȂ�����t����i�E�F���`�̌���j�����{����
9.1�@�����U�̌�������{����2�Q�̕��U�ׂ�
�j���̑̏d�𑪒肵���Ƃ��뉺�̂悤�ȕW�{������ꂽ�i����1���͑���ł��Ȃ������Ƃ���j�B����2�Q�̕ꕽ�ςɍ�������Ƃ����邩�L�m��5���Ō�������{����B
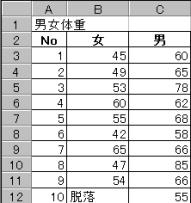
9.1.1�@2�Q�͓����U�ł��邩���肵�m�F����
2�Q�̕��U���F���z�ɏ]���BF���z�͉��̂悤��2�̎��R�x�ɏ]�����z�ł���A�L�m��5%�ŗ������������ƁA����2.5%�_�Ə㑤2.5%�_�Ō��������B�������ϐ�1�̕��U(S12)>�ϐ�2�̕��U(S22)�ƂȂ�悤�ɔ͈͂��w�肷��A�㑤2.5%�_�ׂ邾���ŗǂ��B
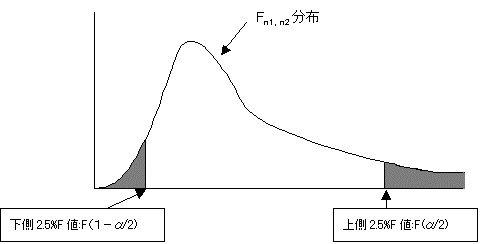
(1)���肷��W�{�f�[�^����͂���B
(2)�c�[�������̓c�[����F����:2�W�{���g�������U�̌����I��
���͗p�{�b�N�X���J������A�ϐ�1�͈̔͂͏����̑̏d�͈̔͂��w�肵�A�ϐ�2�͈̔͂͒j���̑̏d�͈̔͂��w�肷��B������������{����̂ŁA���l��0.025�ɂ���B�o�͐�͓����V�[�g��Ɏw�肷��BOK�{�^�����N���b�N����Ƃ����Ɍv�Z����Č��ʂ��\�������B
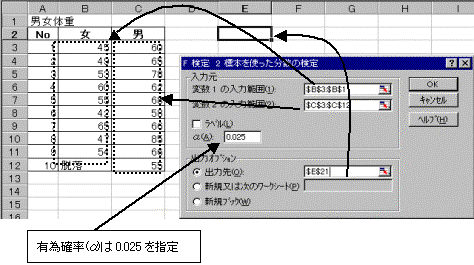
(3)�v�Z���ʂ�����
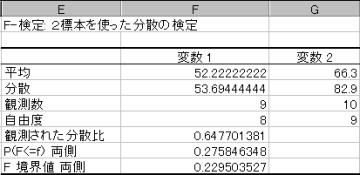
�ϐ�1�̕��U=53.694�ł���A�ϐ�2�̕��U=82.9�ł���B�ϐ�1�̕��U<�ϐ�2�̕��U�ƂȂ��Ă���̂ŁA����2.5%�_���g�p���Č�������{���邱�ƂƂȂ�B�����ŏ㑤2.5%�_���g�p���Č�����s�����߂ɁA�ϐ�1�͈͂ƕϐ�2�͈͂̎w����t�ɂƂ�悤�ɍēx�������蒼���B
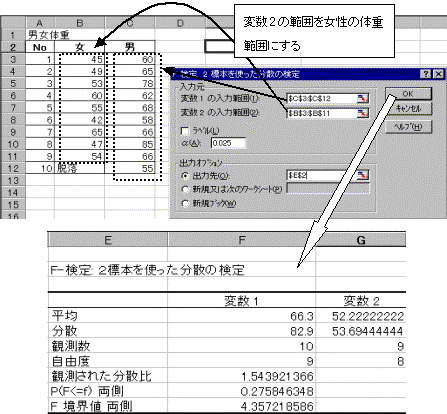
���x�͕ϐ�1�̕��U>�ϐ�2�̕��U�ƂȂ��Ă���̂ŁA�㑤2.5%�_�ׂ�悢�B
(4)��������{
�@����������
�A�������@H0�@��12����22�@�i2�Q�̕ꕪ�U�͓����U�ł���j
�Η������@H1�@��12����22�@�@�i2�Q�̕ꕪ�U�͓����U�ł͂Ȃ��j�@�@
�A���蓝�v�ʂׂ�
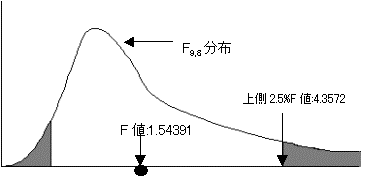
�ϑ����ꂽ���U��iF)��F���z�ɏ]���BF=1.543921366�@1�Ԗڂ̎��R�x:9�A2�Ԗڂ̎��R�x:8�ł���B
�B�L�m��5%�ŗ�����������{:�㑤2.5%�_�ׂ�B
�@�@F=1.54391366��F���E�l:4.357218586�ł���B�˂��Ċ��p��ɓ���Ȃ�����ċA�����������p�ł��Ȃ��B2�Q�͓����U�ł͂Ȃ��Ƃ͂����Ȃ��B
9.1.2�@F�l�Ɋւ����
�@F�l�̊m�������߂��
�@�@�@=fdist(F�l�C���R�x1�C���R�x2)
�@�@�@�@���R�x1:���q�����i�ϐ�1)�@�@���R�x2:���ꕔ��(�ϐ�2)
�A�m������F�l�����߂��
�@�@�@=finv(�m���C���R�x1�C���R�x2)
�B�f�[�^���璼��F��������{�����
�@�@�@=ftest(�ϐ�1�͈́C�ϐ�2�͈�)
�@F���z��2�̎��R�x���g�p����̂ŁA���R�x�̏��Ԃɒ��ӂ��Ȃ���Ȃ�Ȃ��B
�u�����g�p���AF�l�Ɋւ���e��l�����߂Ċm�F�v
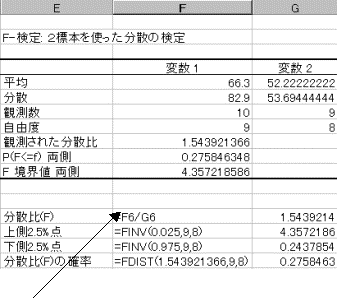
�@���U��iF�l�j�́A�ϐ�1�i�j���̑̏d�j�̕s�Ε��U��ϐ�2�i�����̑̏d�j�̕s�Ε��U�Ŋ������l�ł���B���̕��U��̒l�����Ɍ�����s���B

���R�x1��9�A���R�x2��8�ƂȂ��Ă��邱�Ƃɒ���
�ϑ����ꂽF�l���㑤2.5%�_�����������̂ŁA���p��ɓ���Ȃ��B�A�����������p�ł��Ȃ��B
FTEST�����g�p���āA����F��������{��2�Q�������U�����肷��B
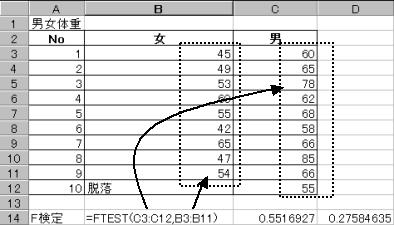
�@�@�@�@�@�@�@�@�@���͂������@�@�@�@�@�@�@�v�Z���ʁ@�@����1/2�l
FTEST���ł́A�Б��m���l���\�������̂ŁA������������{����ɂ͂��̒l��1/2�����l���g�p����B���̏ꍇ�m���l=0.27584635�ł��邩��A���̒l��0.025���傫���̂Ŋ��p��ɓ���Ȃ����Ƃ��킩��B
9.2�@�Ή��̂Ȃ������U2�Q��W�c�̕ꕽ�ς̍��̌���
9.2.1�����U�ł���2�Q��W�c�́u�ꕽ�ς̍��̌���v�����{�c������
��̌���̌��ʁA2�Q�ꕪ�U�́A�����U�ł͂Ȃ��Ƃ͂����Ȃ��̂ŁA�����U�̎���2�Q���K��W�c�́u�ꕽ�ς̍��v�̌�����s���B
������͎��R�x��1�ł���̂ŁA���R�x�̏��Ԃ��C�ɂ���K�v�͂Ȃ��B�ϐ�1�ƕϐ�2�͈̔͂��t�ɂ��Ă��������ʂ�������B
(1)�f�[�^����͂��A���փc�[���Łut����:�����U�����肵��2�W�{�ɂ�錟��v��I����t��������{����B
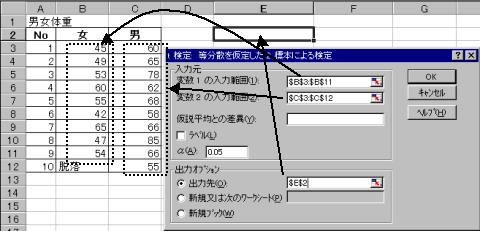
(2)�v�Z���ʂ��m�F
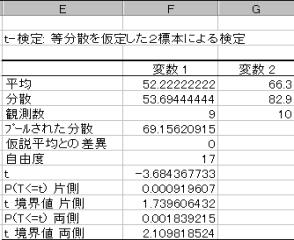
(3)��������{
�@����������@�@
�@�@�@�A�������@H0:���P�����Q�@�i2�Q�̕ꕽ�ς͓������j
�@�@�@�Η������@H1:���P�����Q�@�i2�Q�̕ꕽ�ς͓������Ȃ��j
�A���蓝�v�ʂׂ�
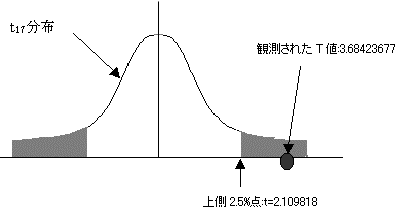
���蓝�v��(T)�͂����z�ɏ]���BT=-3.684367733�BT�l�͐�Βl���g�p����̂Ł@T=3.684367722�ł���B
�B�L�m��5%�Ō��肷��B��������ł���̂ŏ㑤2.5%�_�ׂ�B
 �@�@�@
�@�@�@
�㑤2.5%�_�ׂ�ƁA�ϑ����ꂽT�l=3.684�ł���A���p��ɓ���B�܂����̎��̊m��=0.001839�Ƌ��߂��Ă���A���̒l��0.05��菬�����̂Ŋ��p��ɓ��邱�Ƃ��킩��B
�˂��ċA�����������p����B2�Q�̕ꕽ�ςɍ�������Ƃ�����B
9.2.2�@t����Ɋւ�������g�p���Č�������{
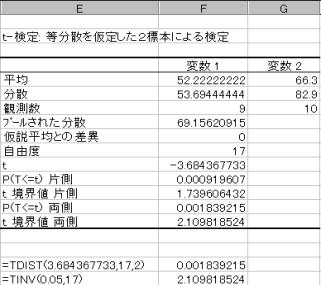
T�l:3.684367733�@���R�x:17�@��������ł̊m����=tdist(t�l�C17�C2)����0.001839215�Ƌ��߂���B���̒l��0.05��菬�����̂Ŋ��p��ɓ��邱�Ƃ��킩��B�����2�Q�̕ꕽ�ς͓������Ƃ����A�����������p����B
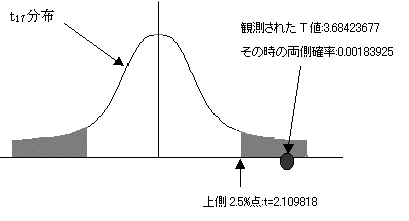
ttest�����g�p���āA�W�{�f�[�^���璼��t�l�m�������߂�B
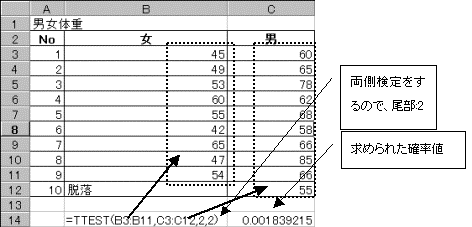
ttest�����g�p���ċ��߂�ꂽ�m���l:0.001839215�ł���A���̒l��0.05��菬�����̂Ŋ��p��ɓ���B����Ēj���Ԃ̑̏d�̕ꕽ�ς͓������Ƃ����A�����������p����B
9.3�@�Ή����Ȃ������U�łȂ�2�Q�̕ꕽ�ς̍��̌���
���{�l�ƃA�����J�l���l�j�q10�l�̃W�����v�͒������s���A���̂悤�Ȍ��ʂ�ꂽ�B���̎��W�����v�͂ɐl��Ԃ̍�������Ƃ����邩�B�L�א���5%�Ō�����s���B
(1)�W�{�f�[�^�����
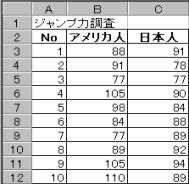
(2)�����U�̌�������{
2�Q�������U�ł��邩�ǂ���������s���B
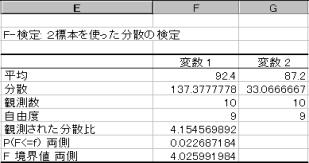
�A�������́u2�Q�̕ꕪ�U�͓����U�v�ł���B�ϑ����ꂽF�l=4.154569892�ł���A���̒l�́AF���E�l=4.025991984�����傫���B�܂��m���l=0.022687184�ł��肱�̒l��0.05�����������B����Ċ��p��ɓ���B2�Q�̕ꕪ�U�͓������Ƃ͂����Ȃ��B2�Q�̕ꕪ�U�͓����U�ł͂Ȃ��B
(3)�����U�łȂ����́u2�Q�̕ꕽ�ς̍��v�̌�������{
(2)����2�Q�̕ꕪ�U�͓����U�łȂ����Ƃ����������̂ŁA2�Q�̕ꕽ�ς̍��̌���́u�����U�łȂ�2�Q�̕ꕽ�ς̍��̌�������{
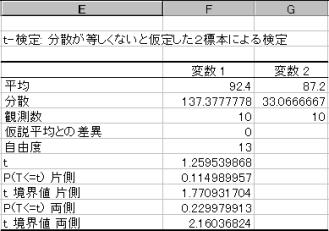
��������{
�@����������@�@
�@�@�@�A�������@H0:���P�����Q�@�i2�Q�̕ꕽ�ς͓������j
�@�@�@�Η������@H1:���P�����Q�@�i2�Q�̕ꕽ�ς͓������Ȃ��j
�A���蓝�v�ʂׂ�
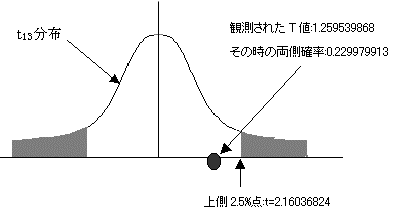
���蓝�v��(T)��t���z�ɏ]���BT=1.259539868�@
�B�L�m��5%�Ō��肷��B��������ł���̂ŏ㑤2.5%�_�ׂ�B
�����E�l����:2.16036824�ł���A�ϑ����ꂽT�l�͂��̒l�����������B�܂��m���l(�����j:0.229979913�ł���A���̒l��0.05�����傫���B����ċA�����������p�ł��Ȃ��B2�Q�̕ꕽ�ς͓������Ƃ����Ȃ����Ƃ͂Ȃ��B
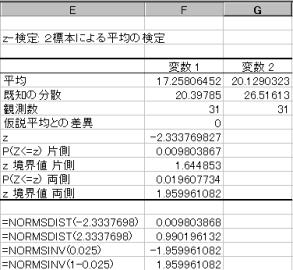
10.�@��W�{�ł̕ꕽ�ς̍��̌���cZ����
��W�{(�W�{��30�ȏ�)�ł́u�ꕽ�ς̍��̌���v�ł�Z������s���B
A�n���B�n��ł���G�߂̈�̐�����(�앨�̒�����)�A���ꂼ��33�̕W�{��ꂽ�B���̌��ʂ���A�n���B�n��̈�̐����ɍ�������Ƃ����邩�L�m��5%�Ō�������{����B
|
�W�{�� |
A�n�� |
B�n�� |
|
1 |
13 |
28 |
|
2 |
21 |
27 |
|
3 |
14 |
25 |
|
4 |
11 |
16 |
|
5 |
12 |
18 |
|
6 |
25 |
33 |
|
7 |
22 |
15 |
|
8 |
28 |
12 |
|
9 |
10 |
22 |
|
10 |
14 |
24 |
|
11 |
18 |
19 |
|
12 |
14 |
22 |
|
13 |
20 |
22 |
|
14 |
13 |
13 |
|
15 |
18 |
12 |
|
16 |
11 |
22 |
|
17 |
12 |
20 |
|
18 |
15 |
14 |
|
19 |
14 |
18 |
|
20 |
19 |
16 |
|
21 |
22 |
17 |
|
22 |
17 |
24 |
|
23 |
21 |
23 |
|
24 |
16 |
22 |
|
25 |
15 |
26 |
|
26 |
18 |
19 |
|
27 |
19 |
21 |
|
28 |
24 |
26 |
|
29 |
22 |
19 |
|
30 |
18 |
16 |
|
31 |
19 |
13 |
|
���U |
20.39785 |
26.51613 |
10.1�@���̓c�[�����g�p���Č�������{
(1)�f�[�^����͂��A���ꂼ��̕��U�����߂�B
�W�{����30�ȏ�ł��邩��A���̕��U�����ꂼ��̕ꕪ�U�Ɛ��肷��B
A�n��̕��U:20.39785�@B�n��̕��U:26.51613
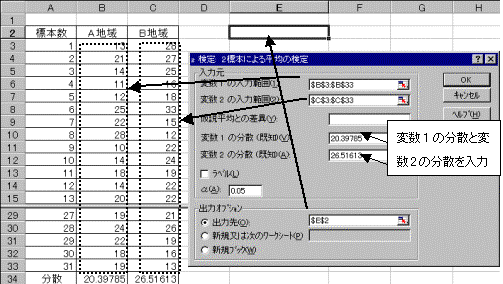 (2)�c�[�����g�p���AZ��������{
(2)�c�[�����g�p���AZ��������{
(3)�v�Z���ʂ��m�F
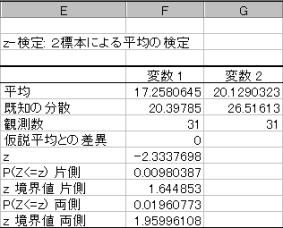
(4)��������{
�@����������@�@
�@�@�@�A�������@H0:���P�����Q�@�i2�Q�̕ꕽ�ς͓������j
�@�@�@�Η������@H1:���P�����Q�@�i2�Q�̕ꕽ�ς͓������Ȃ��j
�A���蓝�v�ʂׂ�
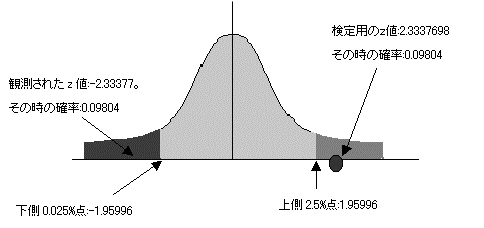
���蓝�v��(z)��Z���z�i�W�����K���z�j�ɏ]���B�㑤�m���l�Ō�����s���ƁAz�l�Ƃ��Ă͂��̐�Βl���g�p����B���蓝�v��:z=2.3337698�@
�B�L�m��5%�Ō��肷��B��������ł���̂ŏ㑤2.5%�_�ׂ�B
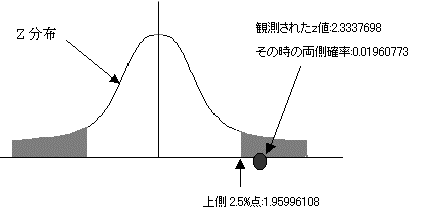
�ϑ����ꂽ���l�́A�y���z�̏㑤2.5�_�����傫���B�܂����̎��̊m���l��0.0196�ł��肱�̒l��0.05�����������B����Ċ��p��ɓ�����B2�Q�̕ꕽ�ς͓������Ƃ����A�����������p����B2�Q�̕ꕽ�ςɂ͍�������Ƃ�����B
10.2�@���l�Ɋւ�����i�W�����K���z�Ɋւ�����j
�@���l����m�������߂�
�@�@�@normsdist(z�l)�@�@=normsdist(-2.3337698)=0.009803868
�A�m������z�l�����߂�
�@�@�@normsinv(�m���l)�@=normsinv(0.025)=-1.959961082�i����2.5%�_)
�@�@�@�@�@�@�@�@�@�@�@�@=normsinv(1-0.025)=1.959961082�i�㑤2.5%�_)