1.�@�ʓI�f�[�^�Ǝ��I�f�[�^
�@�@�f�[�^�͏���\������l�̂��ƂŁA���v�ň����f�[�^�͗ʓI�f�[�^�Ǝ��I�f�[�^�Ƃɕ������B
![]() �ʓI�f�[�^�c�̏d��g���̂悤�ɁA���̒l���̂ɗʂƂ��ĈӖ������f�[�^
�ʓI�f�[�^�c�̏d��g���̂悤�ɁA���̒l���̂ɗʂƂ��ĈӖ������f�[�^
�ʓI�f�[�^�͂���ɔ��ړx�f�[�^�ƊԊu�ړx�f�[�^�Ƃɕ������
![]() ���ړx�f�[�^�c���l�̍��A���l�̔��ɂ��Ӗ��̂���f�[�^
���ړx�f�[�^�c���l�̍��A���l�̔��ɂ��Ӗ��̂���f�[�^
�@�@�@�@�@ �@�@�@�@�@�@�@�@�@�i�g����̏d�Ȃǂ̃f�[�^�j
�@�@�@�@�@ �Ԋu�ړx�f�[�^�c���l�̍��ɂ͈Ӗ������邪�A���l�̔��ɂ͈Ӗ��̂ȃf
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�[�^�i���x�⎎���̐��тȂǂ̃f�[�^�j
���I�f�[�^�c���t�^�⎎���̏��Ԃ̂悤�ɗʓI�Ӗ��������Ȃ��f�[�^
���I�f�[�^�͂���ɏ����ړx�f�[�^�Ɩ��`�ړx�f�[�^�Ƃɕ�������
![]() �@�@�����ړx�f�[�^�c�����Ƃ��ĈӖ������f�[�^
�@�@�����ړx�f�[�^�c�����Ƃ��ĈӖ������f�[�^
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����̐��ь��ʂ̏��Ԃ�A���P�[�g�̌��ʂȂǁj
�@�@���`�ړx�f�[�^�c���t�^��j���̕��ނȂǂ̂悤�ɋ敪���邽�߂̃f�[�^
�@�ʓI�f�[�^�͂��̒l���̂̕��z�͉������̕��z���������A���I�f�[�^�͂��̒l���̓��ʂȕ��z�͎����Ȃ�
2.�@�m�����z
2.1�@�x�����z
�@�@���܁A�Q�O�˂̏����T�O�l�̐g���𑪒肵�A���̑��肵���l�����Ƃɂ��ĉ��\�̂悤�ȓx�����z�\������ꂽ�Ƃ���B
�m �x �� �� �z �\ �n
|
�m�n |
�K���l |
�x�� |
���Γx�� |
�ݐϓx�� |
�ݐϑ��Γx |
|
�P |
146 |
2 |
4% |
2 |
4% |
|
�Q |
150 |
6 |
12% |
8 |
16% |
|
�R |
154 |
12 |
24% |
20 |
40% |
|
�S |
158 |
17 |
34% |
37 |
74% |
|
�T |
162 |
8 |
16% |
45 |
90% |
|
�U |
166 |
3 |
6% |
48 |
96% |
|
�V |
170 |
2 |
4% |
50 |
100% |
|
|
���v |
50 |
100% |
|
|
���̓x�����z�\�̑��Γx�����O���t�����Ă݂�Ɖ��}�̂悤�ɂȂ�B
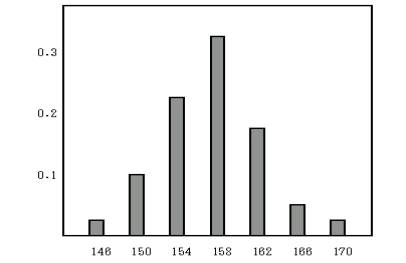
���Γx���́A�e�K���̓x����x�����v�̒l�ɂ���Ċ��������̂ł��邩��A�e���Γx���̍��v�͂P�i�P�O�O���j�ɂȂ�B�܂��e���Γx���͊e�K���̏o�����������Ă���B
�g���P�S�S�`�P�S�Wcm�i�K���l���P�S�Ucm�j�͈̔͂ɑS�̂̂S���̐l�������Ă���A�P�S�W�`�P�T�Qcm�i�K���l���P�T�Ocm�j�͈̔͂ɑS�̂̂P�Q���̐l�������Ă���B���̂��Ƃ́A�����i�o���j����m�����O�D�O�S�A�O�D�P�Q����Ƃ�����B�T���v�����������Ƒ��₵�Ă����ƁA���̃O���t�͒��������������E�ɂ����̍L���������炩�ȋȐ��ɂȂ��Ă���B���̂悤�Ȋm�����z�̋Ȑ����m�����z�Ȑ��Ƃ����A�g���̏o�����̂悤�ɒ������������� �E�ɂ������L���������E�Ώۂ̃O���t�𐳋K���z�Ȑ��Ƃ����B
���K���z��������͎̂��R�E�ɍL�������������Ƃ��ł���B
2.2�@���K���z�c�A�����z�i�A�������l���Ƃ镪�z�j
���K���z�̃O���t�́A���̂悤�ɘA�������Ȑ��̃O���t�ɂȂ�B
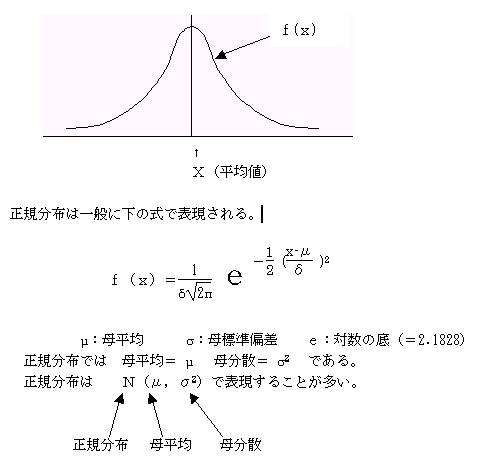
���K���z�̎����A�f�[�^�̕W����������ƁA�ꕽ�ρ��O�C�ꕪ�U���P2�ƂȂ�B���̂悤�ɂ��ā@����ꂽ�Ȑ���W�����K���z�Ȑ��Ƃ����B
�W�����K���z�Ȑ��̎���
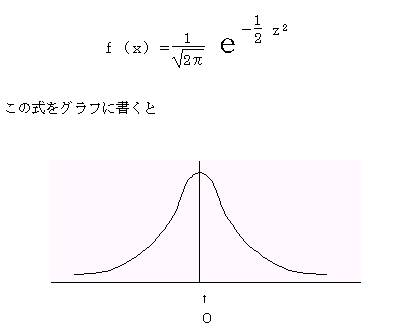
�ꕽ�ρi���O�j�𒆐S�ɂ��č��E�Ώۂ̃O���t�ƂȂ�B
�@�@�@�@�ʏ�W�����K���z�́A�m�i�O�C�P2�j�ŕ\�������B
���K���z��W�����K���z�ɂ���ɂ́A���K���z�̃f�[�^�ix�j��![]() �@ �ŕϊ����邱�Ƃɂ��ꕽ�ρ��O�A�ꕪ�U���P2�̕W�����K���z�ɕς��邱�Ƃ��ł���B
�@ �ŕϊ����邱�Ƃɂ��ꕽ�ρ��O�A�ꕪ�U���P2�̕W�����K���z�ɕς��邱�Ƃ��ł���B
2.3�@�W�����K���z
�@���K���z�̎����A�f�[�^�̕W�������s���A���ϒl���O�F���U���P2 �ɂȂ�悤�ɂ������̂��W�����K���z�ƌĂ�镪�z�ł���B
�@ 

 �W�����K���z�ɂ��ẮA���̐��\�����߂��Ă���A���\���番�z�̒l�i�m���l�j�邱�Ƃ��ł���B
�W�����K���z�ɂ��ẮA���̐��\�����߂��Ă���A���\���番�z�̒l�i�m���l�j�邱�Ƃ��ł���B
�@�@���̖ʐρ��P�i�m�����P�j
�@ ����(x)dx���P
�|�� �O �{��
�@�W�����K���z�ɂ����ẮA���̖ʐϒl���m���l�������Ă���B�W�����K���z�ł́A�ꕽ�����O�E�ꕪ�U���P�ŕ��ϒl�𒆐S�Ƃ������E�Ώۂ̕��z�ł���B
�ʏ�A�W�����K���z�̐��\�ŕ\������Ă���l�́A�O����E���i�{���j�̖ʐϒl���\������Ă���B�܂� �炆(x)dx�̒l���\������Ă���B
2.4�@���K���z�ƕW�����K���z�̓���
�m���K���z�̓����n
�@�����ρF�ʂ𒆐S�Ƃ������E�Ώۂ̕��z�ł���B
�@�@�A�ꕽ�ρF�ʁ@�ꕪ�U�l�F��2�@�ŕ\���B
�@�@�B���K���z�́@�m�i�ʁC��2�j�ŕ\���B
�@�@�C�Q�̊m���ϐ����Ƃ����A�ʁX�ɂm�i��1�C��12�j�A�m�i��2�C��22�j�ɏ]����
�@�@�@���{���̕��z�́A�m�i��1�{��2�C��12�{��22�j�ɏ]��
�@�@�@���|���̕��z�́A�m�i��1�|��2�C��12�{��22�j�ɏ]��
�m�W�����K���z�̓����n
�@�ꕽ�ρ��O�𒆐S�Ƃ������E�Ώۂ̃O���t
�@�@
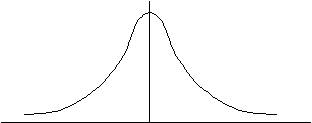
�|�� �O �{��
���E�Ώۂ̋���ł��邩��Az���|������0�܂ł̖ʐς�0����{���܂ł̖ʐς͓������B
�܂��|������{���܂ł̖ʐς͂P�ł���B
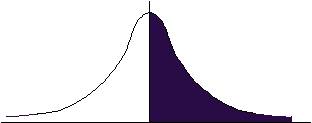 �炆(z)��z �@�@�@ �炆(z)��z
�炆(z)��z �@�@�@ �炆(z)��z

�|�� �O �{��
�炆(z)dz=�炆(z)dz �ł���A�܂� �炆(z)dz���P�@�ł���B
�A�m�����z
�@�@�@�y���炆(z)dz �Ƃ���
(1)z���P�̎�


�@�@�@�@�@�@ �@ �y��0.34134�i�ΐ��̕�����0.34134�j
�@ �@�@-1�@
�@0 +1
�W�����K���z�͍��E�Ώۂ̋���ł��邩��
�|�P��z���P�̊Ԃ̂y�̒l��
0.34134 �~ 2�� 0.68268
�ƂȂ�
���̂��Ƃ́A�W�����K���z�ɏ]�����z�ɂ����ẮA�|�P��z���P�̊ԂɑS�f�[�^��
�@�@�@�@ �U�W�D�Q�U�W��������
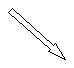
�@(2)�����Q�̎�
���l�� �|�Q�������Q�̊Ԃɂ͑S�f�[�^�̂X�T�D�S�T�����͂���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�y��0.47725

�@�@-2
�@ �@0 +2
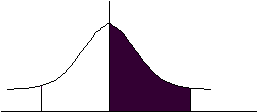
(3)�����R�̎�
���l�� �|�R�������R�̊Ԃɂ͑S�f�[�^�̂X�X�D�V�R�����͂���B
 �@�@�@�@�@ �@�@�@�@
�y��0.49865
�@�@�@�@�@ �@�@�@�@
�y��0.49865
-3 �@
�@0
+3
�m���K���z�ɂ����Ắn
-3�� -2�� -1�� �� �@ �� 2�� 3��
�ʁ|�� �������ʁ{�� �ɑS�f�[�^�̂U�W�D�Q�W��
�ʁ|2�Ё������ʁ{2�ЂɑS�f�[�^�̂X�T�D�S�T��
�ʁ|3�Ё������ʁ{3�ЂɑS�f�[�^�̂X�X�D�V�R�� ���͂���
2.5���K���z�ȊO�̊m�����z
2.5.1�@�Q�����z�c���U���z�i�ƂтƂт̒l���Ƃ镪�z�j
�@�Q�����z�c�a(n�p)�ŕ\���B
�@ ���ܐ�������m�������A���s����m�������Ƃ���ƁB�������邩���s���邩�͂��݂��ɔr�����ۂł��邩��A�����P�|���ł���B���̎����s���Đ�����������Ƃ���ƁA���̐�������m����
n�bx �E��x�E��n-x ��
n�bx �E��x�E�i�P�|���jn-x
�ŕ\�����B
�@�@�@�@�@�@�@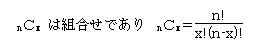
�@ ���̂悤�Ȋm�����z���u�Q�����z�v�ƌĂсA���}�̂悤�ɗ��U�I�ȃO���t�ɂȂ�B
�A�Q�����z�̓���
(1)�Q�����z�ɂ����ẮA����:�ʁ����E�� �@
�@![]()
(2)�Q�����z�ɂ����āA���s��(n) �𑝂₵�čs���ƂQ�����z�͐��K���z�ɋ߂Â��B
��ʂɎ��s��(n)��n��30 �Cn�p��5�̎��ɂ́A���K���z�ŋߎ����邱�Ƃ��ł���B(���v���X�̒藝�j
�a(n,p)�́@�m�i�ʁC��2�j���m�in�p�Cn�p�q�j�ŋߎ��ł���B
�@�@�@�@�@�@�@ �� ��
���ϒl �W����
�@ ���s��
�@ ���₵�Ă���
![]()
�@ �a�in�Cp�j
�m�in�p �Cn�p�q�j
�@�Q�����z
���K���z
2.5.2�@��2 ���z�E�����z�E�e���z�c�W�{���z�i���K��W�c���璊�o�����W�{�̕��z�j
�@ ���K��W�c���璊�o�����W�{�̕��z�ɂ��āA��2 ���z�E�����z�E�e���z�Ƃ����d�v�Ȋm�����z������B
�@��2���z
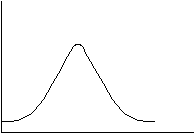
�@X1,X2,�cXn �����݂��ɓƗ��ŁA�W�����K���z�E�m�i�O�C�P2�j�ɏ]�����A���̕����a�͎��R�xn�̃�2���z�ɏ]���B
��2�� X12+X22+�c+Xn2 = ��Xi2 �͎��R�xn�̃�2 ���z�ɏ]��
�����R�x�Ƃ́A���R�ɓ�����ϐ��̌��������i�Ɨ������ϐ��̌��j
����2 ���z�͎��R�x�Ɉˑ����镪�z�ł���B���R�x���ς��Ƃ��̕��z���ς��B
�m��2 ���z�̓����n
��2���z�́A���R�x�Ɉˑ����镪�z�ł���A��W�c�̕��U�̌���␄��Ɏg�p����镪�z�ł���B
(1)���R�x�id.f�j��n�Ƃ���ƁA���ϒl�Fn�@���U�F2n�ł���
(2)��12 �� X12
+ X22 + �c + Xn2����Xi2 �����R�x���̃�2 �ɏ]��
�@
��22 �� X22
+ X22 + �c + Xm2����X22 �����R�x���̃�2 �ɏ]����
��12�{��22 �̕��z�͎��R�xm�{n�̃�2 ���z�ɏ]��
(3)���R�x�P�̃�2 ���z�ƕW�����K���z�y�Ƃ̊Ԃɂ�
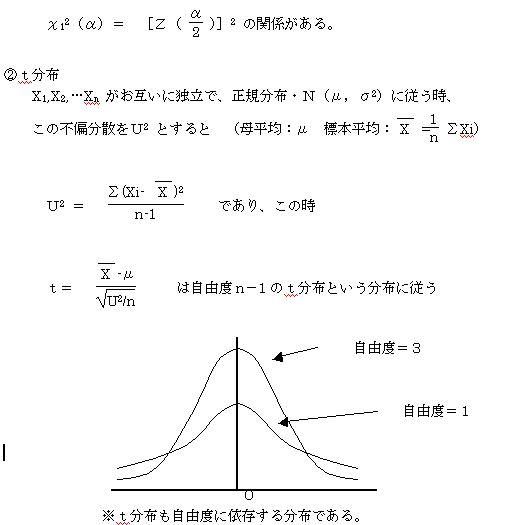
�m�����z�̓����n
�����z�͕W�����K���z�m�i�O�C�P2�j�Ɏ������z�ŕ��ϒl�F�O�𒆐S�ɂ������E�Ώۂ̕��z�ł���B�����z�͕�W�c�̕��ς̌���␄��Ɏg�p�����B
(1)���R�x�id.f�j��n�Ƃ���ƁA���ϒl�F0�in��2)�@���U�Fn/(n-2)�@(n��3)�ł���B
(2)n��30�̎��ɂ́A�W�����K���z�m�i�O�C�P2�j�ŋߎ��ł����B
�B�e���z
�@X1,X2,�cXn1 �����݂��ɓƗ��ŁA�W�����K���z�E�m�i��1�C��12�j�ɏ]��
�@Y1,Y2,�cYn2 �����݂��ɓƗ��ŁA�W�����K���z�E�m�i��2�C��22�j�ɏ]����
���ꂼ��̕s�Ε��U���t12�A�t22 �Ƃ����
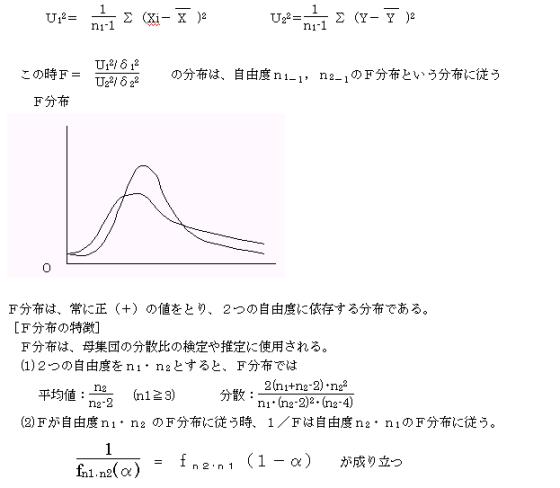

3.��W�c�ƕW�{�ɂ���
3.1�@��W�c�ƕW�{
�@��W�c�Ƃ́A���v�ɂ����Ē����̑ΏۂƂ���S�Ẵf�[�^�̏W�܂�������B�Ⴆ�A���{�l�̂Q�O�˂̒j���̐g���̃f�[�^�ׂ����Ƃ���ƁA���{�l�̂Q�O�˒j�q�̐g���S�Ă���W�c�ƂȂ�B��W�c�ɂ́A�L����W�c�Ɩ�����W�c�Ƃ�����B���{�l�̂Q�O�˒j�q�̐g���ƂȂ�ƗL����W�c�Ƃ������ƂɂȂ�B�܂��A�R�C���𓊂��ĕ\���ł邩�����ł邩�̊m�����z��A�������Ђ��ē�����m���̕��z�Ȃǂ͖�����W�c�ł���B
�@�L����W�c�ł�������W�c�ɂ��Ă��A���̕�W�c�̑S�Ă��W�߂đ��肷�邱�Ƃ͕s�\�ł���B���̂��߂ɁA��W�c�̎����Ă��鐫�������Ȃ��悤�ɂ��āA��W�c���疳��ׂɃf�[�^�𒊏o���W�߂��f�[�^���u�W�{�v�ƌĂԁB���̕W�{�ɂ��Ē������邱�Ƃ��u�W�{�����v�ƌĂсA�W�{�����̌��ʓ���ꂽ�������Ƃɂ��ĕ�W�c�Ɋւ��������@�Ƃ��āA�u����v�E�u����v�̂Q�̕��@������B
3.2�@�ꐔ�ɂ���
�@��W�c�̓��v�ʂł��镽�ϒl�F�ʁE���U�F��2 �Ȃǂ̂��Ƃ�ꐔ�ƌĂсA���̂��ăƂŕ\�����Ƃ������B��ʂɕꐔ�i�Ɓj�͒��ڋ��߂邱�Ƃ��ł��Ȃ��̂ŁA�W�{�f�[�^���琄�肷�邱�Ƃ������B

3.3�@����
�@��ʂɕꐔ�Ƃڋ��߂邱�Ƃ͂ł��Ȃ��B���̂��ߕW�{���Ƃ�A���̕W�{�ׂ邱�Ƃɂ��ꐔ�i�Ɓj�𐄒肷��B���́u����v�̕��@�ɂ́A�ꐔ���̂��̂̒l�𐄒肷��u�_����v�Ƃ���M����Ԃ�݂��Đ��肷��u��Ԑ���v�Ƃ�����B�_����̕����ꐔ���̂��̂̒l�𐄒肷��̂ŕ�����₷�����A���v�I�ɂ͂���M����Ԃ�݂��Đ��肷��u��Ԑ���v��p����ꍇ�������B
�@�ꐔ�i�Ɓj�𐄒肷�鎞�A�W�{�f�[�^�����Ƃɐ��肷�邪�A���̎�����Ɏg�p������̂��������̒l�ɕ�Ȃ�����ʂł���Ƃ����Ӗ��Łu�s�ΐ���ʁv�Ƃ������̂��g�p����B�悭�g�p����s�ΐ���ʂƂ��ẮA�u�s�ΐ��蕪�U�v������B
�@���܁A��W�c�̕��ϒl�F�ʁE���U�F��2�Ƃ���ƁA���̕�W�c���疳��ׂɂ����o�����W�{�i�W�{�̑傫���F���Ƃ����j�̕��ϒl�F![]() �E���U�F�r2�Ƃ���ƁA�s�Ε��U�t2��
�E���U�F�r2�Ƃ���ƁA�s�Ε��U�t2��
![]()
3.4�@���S�Ɍ��藝
�@�@��W�c�i�ꕽ�ρF�ʁ@�ꕪ�U�F��2 �j���疳��ׂɂ����o�����W�{�̕��ρ�![]() �̕��z�W�{�����̕��z�j���݂�ƁA�����[���ɑ傫����A���̕W�{���ς̕���
�̕��z�W�{�����̕��z�j���݂�ƁA�����[���ɑ傫����A���̕W�{���ς̕���![]() �͕ꕽ�ρi�ʁj�ɓ������A���̕��U�̓�2 �^���ƂȂ�B���̂��Ƃ́A��W�c�̕��z�̎�ނɊW�Ȃ���������B
�͕ꕽ�ρi�ʁj�ɓ������A���̕��U�̓�2 �^���ƂȂ�B���̂��Ƃ́A��W�c�̕��z�̎�ނɊW�Ȃ���������B
![]()
 �W�{����
�W�{����![]() �̕��z
�̕��z
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��W�c�̕��z

���F�ꕽ��
����W�c���璊�o�����W�{����![]() �̕��z�́A�ꕽ�ρi�ʁj�𒆐S�Ƃ��Ă��̕t�߂ɏW�܂��ĕ��z����B
�̕��z�́A�ꕽ�ρi�ʁj�𒆐S�Ƃ��Ă��̕t�߂ɏW�܂��ĕ��z����B
��W�c�i���ρF�ʁ@���U�F��2 �j���疳��ׂɂ����o�����W�{�̕W�{����![]() �̕��z�́A����������x�傫����ߎ��I�ɐ��K���z�m�i�ʁC��2 �^���j�ɏ]���B������u���S�Ɍ��藝�v�Ƃ����B
�̕��z�́A����������x�傫����ߎ��I�ɐ��K���z�m�i�ʁC��2 �^���j�ɏ]���B������u���S�Ɍ��藝�v�Ƃ����B
�܂��A�f�[�^��W��������
�@�@�@
4.�@����
�@ ��W�c�ɂ��Ă��̃f�[�^�S�Ă��W�߂邱�Ƃ͕s�\�ł���B�����ŕ�W�c�̕ꐔ�̏��ɋ߂Â����߂̕��@�Ƃ��ĂQ�̕��@������B�P�́A����ł���A�����P�́u����v�ƌĂ����@�ł���B����Ƃ́A��W�c���疳��ׂɒ��o�����W�{�ɂ��āA���ς╪�U�Ȃǂ����߁A���̕W�{���瓾���ď������Ƃɂ����A��W�c�̕ꐔ�̒l�𐄒肵�Ă����B����u����v�Ƃ́A�ŏ��ɕꐔ�ɂ��Č��_�ł���u�����v�����ĂāA���ɕW�{���瓾��ꂽ�������Ƃɂ��Č���̂��߂́u���v�ʁv�����߂�B���̓��v�ʂ����̊m�����z�ɏ]���̂ŁA�m�����z�ׂ��炩���ߐݒ肵��������艼���̔�������m�����������悤�ł���A�����ŕꐔ�ɑ��Č��߂����Ƃ���́A�ő��ɋN���蓾�Ȃ����Ƃł���Ɣ��f���āA�����̐ݒ肪�Ԉ���Ă����Ƃ��āu�����v�����p���A�����ɑΗ��������̗p������@���Ƃ�B
4.1�@����̕��@
�@����������
�@�ꐔ�ɑ��Ă��鉼�������Ă�B���ʉ����͗]��N���蓾�Ȃ����Ƃ�z�肵�Ă��Ă邱�Ƃ������A���p����邱�Ƃ�O��ɂ��Ă��Ă�̂ŁA���̊��p��O��ɂ��Ă��Ă��鉼���̂��Ƃ��u�A�������F�g0�v�Ƃ����B���̋A�������ɑ��Ă��Ă��鉼���̂��Ƃ��u�Η������F�g1�v�Ƃ����B�ʏ�A�������͂߂����ɋN���蓾�Ȃ��Ƃ��Ċ��p���A�����ɑΗ��������̑�����Ƃ������@���Ƃ�B�i�ȉ��{���ł͋A��������P�ɉ����Ƃ���j
�A���蓝�v�ʂ����߂�B
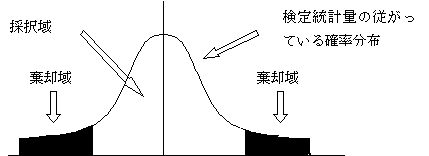
�@��W�c�̕ꐔ�ɑ��Ă��Ă���u�����F�A�������v���̑����邩���p���邩���f����ڈ��ƂȂ�̂��u���蓝�v�ʁv�ƌĂ����̂ł���B���蓝�v�ʂ́A��W�c���疳��ׂɒ��o�����W�{�̃f�[�^�����Ƃɂ��ċ��߂�B�܂��A���߂����蓝�v�ʎ��̂��m���ϐ��ł��邽�߂ɉ��炩�̊m�����z�ɏ]���B���蓝�v�ʂ̊m�����z��������A���������p���邩�̑����邩���f���邱�Ƃ��ł���B
�B�L�א��������߂�
�@���蓝�v�ʂ̊m�����z������������A�������̑����邩���p���邩���f���邽�߂̊�Ƃ��Ĉ��̊m���̒l�����߂�B���̒l�̂��Ƃ��u�L�א����v�ƌĂԁB�W�{���狁�߂����蓝�v�ʂ̒l���L�א����Ō��߂��̑���i�������̑�����̈�F�����̂悤�Ȃ��Ƃ͂��蓾�邱�ƂƔ��f����̈�j�ɓ����Ă���A�������̑�����B�����i�g�O�j��ϋɓI�ɍ̗p����킯�ł͂Ȃ������܂ł́u�A�����������p���邱�Ƃ͂ł��Ȃ��v�Ƃ��āA�A�����������ɓI�ɍ̗p����B�܂����p��i���������p����̈�F�����̂悤�Ȃ��Ƃ͖ő��ɋN���蓾�Ȃ����ƂƔ��f����̈�j�ɂ͂���悤�ł���A���������p�������ɑΗ�����(�g1)��ϋɓI�ɍ̑�����B
�� �@�@�@ ��
�L�א����@�@�@�@�@�@�@�@�@�L�א���
4.2�@��������ƕБ�����
�@�@�����́u���p��v���A���蓝�v�ʂ̏]���Ă���m�����z�̗����ɂ�����̂��u��������v�Е������ɂ�����̂��u�Б�����v�Ƃ����B
(1)��������
�@��������������Ȃ����́A���肵���l���u����l�v�ɓ������Ƃ��������Ȃ��Ƃ��A�܂��͑S���\�z�ł��Ȃ����ɂ����Ȃ��B
���ܗL�א��������ŕ\���ƁA�̑���́u�P�|���v�ŁA���p��́u���v�ł���B���̎����p��͍��E�����ɂ���̂ŁA���ꂼ�ꍶ�E�̃��^�Q�_�ׂĊ��p���ݒ肷��B

�� �@�@�@ ��
�L�א����@�@�@�@�@�@�@�@�L�א���
(2)�Б�����
�@�@���Б�����
���Б�������s�����́A�ꐔ������l��菬�������ǂ������肷�鎞�ɍs���B
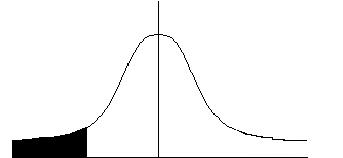 ���Б�����́A���p�悪�����ɂP����B�L�א��������Ƃ���ƁA���p��͍������_�ł���B
���Б�����́A���p�悪�����ɂP����B�L�א��������Ƃ���ƁA���p��͍������_�ł���B


�@�@
�@�@�@�@�@�@�@�@�@ ��
�L�א����@�@
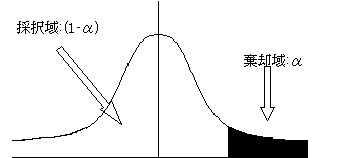
�A�E�Б�����
�E�Б�������s�����́A�ꐔ������l���傫�����ǂ������肷�鎞�ɍs���B
���Б�����́A���p�悪�E���ɂP����B�L�א��������Ƃ���ƁA���p��͉E�����_�ł���B
�@�@�@�@�@�@�@�@�@ �@ ��
�@�@�@�@�@�@�@�@�@�@ �@�L�א����@�@
4.3�@����ɂ�����Q��ނ̌��
��P��̌��c�������������i�^�j�Ȃ̂Ɋ��p������B���̂悤�Ȍ�������m�������ŕ\���B���̃��͗L�א����Ɠ����ɂȂ�B
��Q��̌��c�������ԈႢ�i�U�j�Ȃ̂ɍ̗p������B���̂悤�Ȍ�������m�������ŕ\���B
�ȏ�̊W��\�ɂ����
|
|
����ɂ��̑� |
|
|
�g0���^ |
�g0���̑�(������) �P�|�� |
�g1���̑�(��P��̌��) �� |
|
�g0���U |
�g0���̑�(��Q��̌��) �� |
�g1���̑�(������) �P�|�� |
��P��̌�������m���̓��A��Q��̌�������m���̓��ł���B�ǂ���̌����������������킯�ł��邪�A��������������ƃ����傫���Ȃ�A��������������ƃ����傫���Ȃ�W������B
�@�����Ń��ƃ��������Ɍ��߂�������ł��邪�A�ǂ���̌�肪���������ɔ������鑹�����傫�������ׂāA�������鑹��������������悤�Ɍ��߂�K�v������B�܂�A��P��̌������邱�Ƃɂ�蔭�����鑹�����傫�����ɂ̓������������A��Q��̌������邱�Ƃɂ�蔭�����鑹�����傫�����ɂ̓�������������悤�ɂ���B
�@�������A�ʏ퉼���i�g0�j�́A�̗p����Ȃ����Ƃ�O��ɂ��Ă�i�g0���U��O��j�̂ŁA��P��̌�����������A��Q��̌������邱�Ƃ����d�v�ł���B�����ŁA�����ł��邾�����������Č�������s����B�������A���܂胿������������Ƒ�Q��̌�������m�����傫���Ȃ��Ă��܂��̂ŁA�ʏ탿��5% ���1% �Ō��肷�邱�Ƃ������B
�@��ʂɕW�{���𑝂₵�Ă����ƁA���̃f�[�^�͒��S�Ɍ��藝�ł����炩�Ȃ悤�ɕꕽ�ρi�ʁj�̕t�߂ɏW�܂��Ă���̂ŁA��P��̌��i���j�Ƒ�Q��̌��i���j���Ƃ��ɏ���������ɂ́A�W�{���𑝂₷�Ƃ悢�B
5.�@�ꕽ�ς̍��̌���
5.1�@�Q�Q�̕ꕽ�ς̍��Ɋւ��錟��
�@�@�Q�Q�̕ꕽ�ς̍��Ɋւ��錟��ނ����
�i�T�j�Q�Q�̕�W�c�����K���z�ɏ]����
�@�@�@(1) �Q�Q�̕�W�c���Ή��̂Ȃ���
�@�@�@�@ �@�Q�Q�̕�W�c�̕ꕪ�U���������Ă��鎞�c�y����
�@�@�@�@�@�A�Q�Q�̕�W�c�̕ꕪ�U�͕s�����������U�Ɛ���ł��鎞�c������
�i�����U�̌���c�e����j
�@�@�@�@�@�B�Q�Q��W�c�̕ꕪ�U���s���ł������U�Ɛ���ł��Ȃ����c�E�F���`�̌���
(2) �Q�Q��W�c���Ή��̂��鎞�c������
���y����́A�W�����K���z�𗘗p��������B������́A�����z�𗘗p��������
���e����́A�e���z�𗘗p��������
�Q�Q��W�c���Ή��̂��鎞�ƂȂ����Ƃ́A�ΏۂƂ����W�c���y�A�W�ɂ��邩�Ȃ����̈Ⴂ�ł���B�Ή��̂���Q�Q��W�c�Ƃ́A��u����O�ƌ�̐��т̕ω��Ƃ��A������ޑO�ƌ�ł̑̒��̕ω��̂悤�Ƀy�A�W�ɂ���ꍇ�������B�܂��A�j���̈Ⴂ�ɂ��g���̈Ⴂ�Ȃǂ̂悤�Ƀy�A�W�̂Ȃ��Q�Q�������B
���W�{�����傫�����i30�W�{�ȏ�j�͕ꕽ�ς̍��̌���ł�Z������s��
�i�U�j�Q�Q��W�c�����K���z�ɏ]��Ȃ����c�m���p�����g���b�N������s���B
�@�@�@(1)�Q�Q��W�c���Ή��̂Ȃ����c�E�B���R�N�X���̏��ʌ���
�@�@�@(2)�Q�Q��W�c���Ή��̂��鎞�c�E�B���R�N�X���̕����t�����ʌ���
�m�m���p�����g���b�N����ɂ��āc���I�f�[�^�̏����n
�@�ʓI�f�[�^�́A���̒l���̂ɈӖ�������A������̕��z�ɏ]���Ă���B����𗘗p���Đ���⌟������{����B���������I�f�[�^�́A�j���Ƃ��D�������Ƃ��ŁA���̒l�͒P�Ȃ�敪�⏇�ʂȂǂł�����̕��z�ɏ]���Ă���킯�ł͂Ȃ��B���̂悤�Ȏ��I�f�[�^�̌�����s���̂��m���p�����g���b�N����ƌĂ����̂ł���B
�m���p�����g���b�N����́A������̕��z�ɏ]��Ȃ��u����p�̗ʓI�f�[�^�v�����ʓ��̎��I�f�[�^�ɕϊ����A���I�f�[�^�ɕϊ��������̂��猟�蓝�v�ʂ����߂�B���̌��蓝�v�ʂ͂�����̊m�����z�ɏ]���̂ł���𗘗p���Č�����s�����Ƃ��ł���B
�m���p�����g���b�N����ɂ́A�u��2 ����F�Ɨ����̌���A�K���x����v��u���ʌ���F�E�B���R�N�X���̏��ʌ����N���X�J���E�E�H���X�̏��ʌ���v��������B
5.2�@�R�Q�ȏ�̕ꕽ�ς̍��Ɋւ��錟��
�@�@�@�R�Q�̕ꕽ�ς̍��Ɋւ��錟��ނ����
�i�T�j�ϓ��v�����P�l����i�f�[�^�ɂ����^����v�����P�j
�@�@�@(1) �f�[�^�����K���z�ɏ]�����c�ꌳ�z�u���U����
�@�@�@�@�@���ꌳ���U���͎��{�������ʕꕽ�ςɍ�������Ɣ���������
�@�@�@�@�@�@�ǂ̌Q�Ƃǂ̌Q�ɍ������邩�c���d��r�i��ݥ̪۰Ƃ̕��@�E��̪�̕��@�j
�@�@�@(2) �f�[�^�����K���z�ɏ]��Ȃ����c�N���X�J���E�E�H���X�̏��ʌ���
�@�@�@�@�@���N���X�J���E�E�H���X�̏��ʌ���̌��ʕꕽ�ςɍ�������Ɣ���������
�@�@�@�@�@�@�ǂ̌Q�Ƃǂ̌Q�ɍ������邩�c���d��r�i��ݥ̪۰Ƃ̕��@�E��̪�̕��@�j
�i�U�j�ϓ��v�����Q�l����i�f�[�^�ɂ����^����v�����Q�j
�@�@(1)���ݍ�p���ʂ��Ȃ���
�@�@�@�@�@ �f�[�^�����K���z�ɏ]�����@�@�c�J��Ԃ��̂Ȃ��Q���z�u���U����
�@�@�@�@�@ �f�[�^�����K���z�ɏ]��Ȃ����c�t���[�h�}���̏��ʌ���
�@�@�@(2)���ݍ�p���ʂ����鎞�c�J��Ԃ��̂���Q���z�u���U����
�@�R�Q�ȏ�̕ꕽ�ς̍��̌�������s���鎞�ɂ́A�u�Q�Q�̕ꕽ�ς̍��̌���v���J��Ԃ����s����悢���A�Q������������Ɖ�����J��Ԃ��u�Q�Q�̕ꕽ�ς̍��̌���v���s��Ȃ���Ȃ�Ȃ��B���̂悤�Ȏ��A�u�P���z�u���U���́v�E�u�Q���z�u���U���́v�����s����P��̌���ŕ����̌Q�Ԃ̕ꕽ�ςɍ������邩�ǂ������肷�邱�Ƃ��ł���B�������A�f�[�^�����K���z�ɏ]��Ȃ����ɂ́A�m���p�����g���b�N����̈��ł���u�N���X�J���E�E�H���X�̏��ʌ���v��u�t���[�h�}���̏��ʌ���v�������Ȃ������̌Q�Ԃ̕ꕽ�ς̍��̌���������Ȃ��B
�@�ꌳ�z�u���U���͂����s����ƁA�����̌Q�Ԃ̕ꕽ�ςɍ������邩�ǂ������肷�邱�Ƃ��ł��邪�A�ǂ̌Q�Ƃǂ̌Q�̕ꕽ�ςɍ������邩�ǂ����͕s���ł���B���̂悤�ɂǂ̌Q�Ƃǂ̌Q�ɍ������邩���肷��ɂ́u�ꕽ�ς̑��d��r�v������K�v������B���d��r�̕��@�ɂ́A�u�{���E�t�F���[�j�̕��@�v��u�V�F�t�F�̕��@�v��������B
5.3�@�ꕽ�ς̍��̌���菇