2. EXCELによる重回帰分析
ある会社の8店舗について、その店舗ごとの店員の充実度(X1)・売り場面積(X2)・商品充実度(X3)を10点評価で調査し、またそれぞれの店の月平均売上高について調べて表にしたものが下の表である。
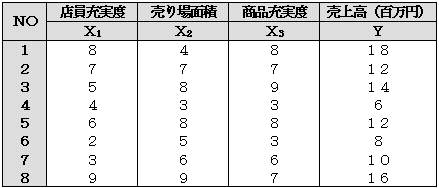
以上の表をもとにして、X1~X3の3要素と売上高(Y)との間に何らかの関係があるかを重回帰分析を実行し調べる。
重回帰分析を実行するには、まず分析用のデータをシートに入力しておく。データを入力後、重回帰分析を実行する。
目的変量は売上高(Y)であり、説明変量はX1~X3の3変量である。
2.1 重回帰式を求める。
重回帰式を、Y=b1・x1+b2・x2+b3・x3+b0 とする。
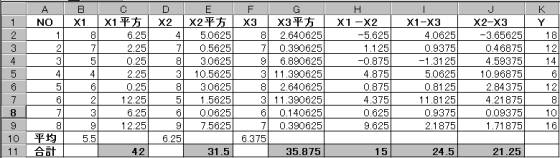
2.1.1 偏差平方和・偏差積和を求める
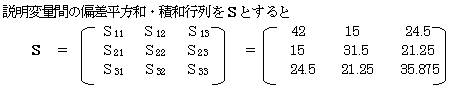
説明変量間の偏差平方和・積和行列をSとすると
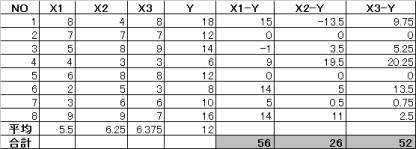
各説明変量と目的変量との偏差積和行列は
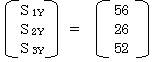
これより
![]() 42b1+15b2+24.5b3=56
42b1+15b2+24.5b3=56
15b1+31.5b2+21.25b3=26
24.5b1+21.25b2+35.875b3=52
b1=0.8161
b2=-0.2749 b3=1.055
b0=12-(0.816×5.5-0.2749×6.25+1.055×6.375)=2.504
よって求める重回帰式は、Y=0.8161X1-0.2749X2+1.055X3+2.504
2.1.2 標準偏回帰係数を求める。
母集団に対する標準偏差を、関数 =STDEVP(範囲)で求める。
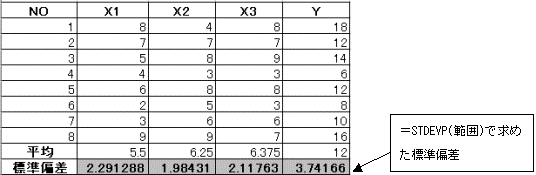

標準偏回帰係数の値から、目的変量に与える影響は変量X3が最も大きく、次に変量X1である。
2. 1.3 予測値と残差を求める。
予測式は、Y=0.8161X1-0.2749X2+1.055X3+2.504
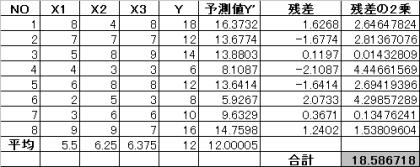
2.1.4 偏回帰係数の標準誤差(SE)を求める。
残差平方和(SE)は、SE=18.587 また不偏分散VE=18.587÷4=4.647
偏差平方和・積和行列をSとすると
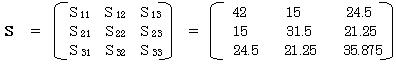
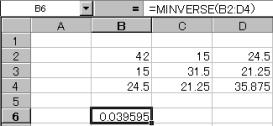
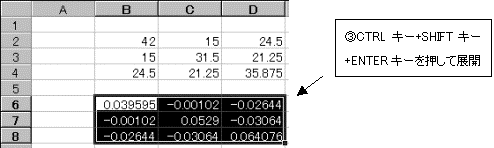
その逆行列S-1 を求める。
(1)=MINVERSE(範囲)関数で、先頭の値を求める。
(2)求めた先頭の値を展開する。


2.1.6 重相関係数の値を見ると非常に正の相関が高そうである。そこで母相関係数をρとして、無相関の検定を行う。
検定統計量をFとすると
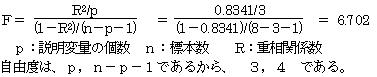
(1)仮説をたてる
帰無仮説 H0:ρ=0(無相関である)
対立仮説 H1:ρ≠0(無相関ではない)
(2)検定統計量F=6.702 は自由度 3,4 のF分布に従う。
(3)有為水準α=0.05 で検定を行う。
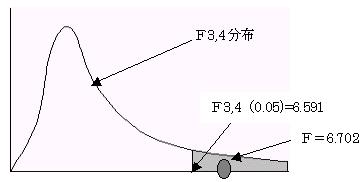
F=6.702>F3,4(0.05)=6.591 であり棄却域にはいる。よって帰無仮説H0:ρ=0を棄却する。母相関係数≠0であり、相関があるといえる。
2.7 自由度調整済重相関係数を求める。
自由度調整済重相関係数をR’、自由度調整済決定係数をR’2とすると

2.8 求めた重回帰式の信頼性を検定する。
![]() 全変動(ST)=112
自由度:8-1=7
全変動(ST)=112
自由度:8-1=7
回帰による変動(SR)=93.4163 自由度:3
残差による変動(SE)=18.5867
自由度:8-3-1=4
以上から分散分析表を作成すると

無相関の検定と同様の結果を得られる。求めた重回帰式は予測に役立つといえる。
2.8.1 偏回帰係数の信頼性を検定する
求めら重回帰式は信頼性があると検定で明らかになったので、次に重回帰式の偏回帰係数の有効性を検定する。偏回帰係数biを検定する。
検定統計量をFとすると
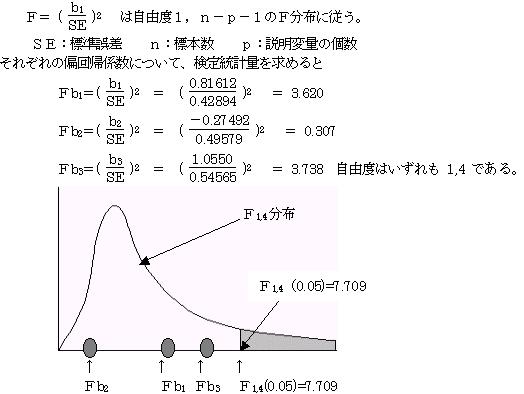
いずれも棄却域に入いらない。帰無仮説(母偏回帰係数β1・β2・β3=0)を棄却できない。
重回帰式は信頼性があるが、それぞれの偏回帰係数の有効性があるといえない。
2.8.2 偏相関係数を求める
偏相関係数は、説明変量Xiと目的変量との相関係数であり、他の説明変量の影響を取り除いたものである。どの説明変量が、目的変量と一番関係が深いかを知ることができる。
説明変量Xiと目的変量との偏相関係数を求める。
単相関係数行列をRとすると
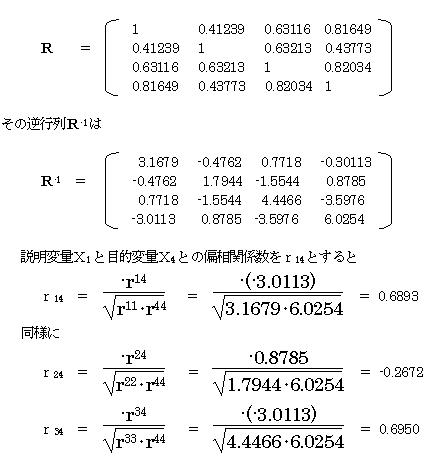
偏相関係数を見ると、r34=0.6950
であり、変量X3 と目的変量の関係が一番深いことが分かる。
2.9 回帰分析ツールの使用
2.9.1 Excelには、分析用ツールとして回帰分析ツールが備わっている。この回帰分析ツールを使用すえると、分析したいデータの入力されている範囲を指定するだけで、回帰分析を実施してくれる。
(1)データ入力後 → ツール → 分析ツール → 回帰分析をクリックして選択
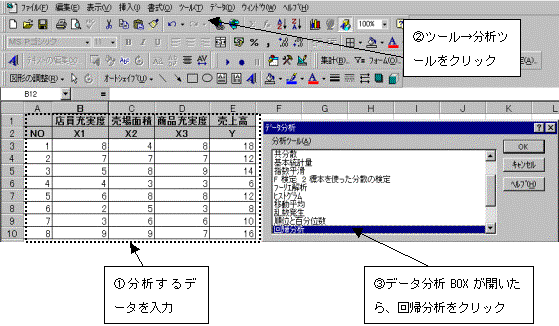
(2)分析するデータの範囲を指定
入力Yは目的変量のデータ範囲を指定(常に1列データ範囲)、入力Xは説明変量範囲(連続した列の範囲)先頭行をラベルとして使用する時は、ラベルの項目をクリック。分析結果を表示する位置を指定する。また何の分析を実施するかをクリックしてチェックする。すべての指定が終了したら、OKボタンをクリック。
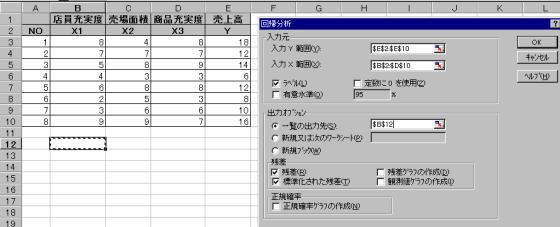
(3)一覧の出力先として指定したセル(B12)以降に分析結果が表示される。
|
概要 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
回帰統計 |
|
|
|
|
|
|
|
|
|
重相関 R |
0.91326 |
|
|
|
|
|
|
|
|
重決定 R2 |
0.83405 |
|
|
|
|
|
|
|
|
補正 R2 |
0.70958 |
|
|
|
|
|
|
|
|
標準誤差 |
2.15562 |
|
|
|
|
|
|
|
|
観測数 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
分散分析表 |
|
|
|
|
|
|
|
|
|
|
自由度 |
変動 |
分散 |
観測された分散比 |
有意 F |
|
|
|
|
回帰 |
3 |
93.413 |
31.138 |
6.701077754 |
0.04869 |
|
|
|
|
残差 |
4 |
18.587 |
4.6467 |
|
|
|
|
|
|
合計 |
7 |
112 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
係数 |
標準誤差 |
t |
P-値 |
下限 95% |
上限 95% |
下限 95.0% |
上限 95.0% |
|
切片 |
2.50414 |
2.7503 |
0.9105 |
0.41406029 |
-5.1319 |
10.1401 |
-5.1319 |
10.1401 |
|
X1 |
0.81612 |
0.4289 |
1.9027 |
0.129839733 |
-0.3748 |
2.00704 |
-0.3748 |
2.00704 |
|
X2 |
-0.2749 |
0.4958 |
-0.555 |
0.6087767 |
-1.6515 |
1.10163 |
-1.6515 |
1.10163 |
|
X3 |
1.05497 |
0.5457 |
1.9334 |
0.125323541 |
-0.46 |
2.56996 |
-0.46 |
2.56996 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
残差出力 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
観測値 |
予測値: Y |
残差 |
標準残差 |
|
|
|
|
|
|
1 |
16.3732 |
1.6268 |
0.9984 |
|
|
|
|
|
|
2 |
13.6773 |
-1.677 |
-1.029 |
|
|
|
|
|
|
3 |
13.8801 |
0.1199 |
0.0736 |
|
|
|
|
|
|
4 |
8.10878 |
-2.109 |
-1.294 |
|
|
|
|
|
|
5 |
13.6413 |
-1.641 |
-1.007 |
|
|
|
|
|
|
6 |
5.9267 |
2.0733 |
1.2724 |
|
|
|
|
|
|
7 |
9.63282 |
0.3672 |
0.2253 |
|
|
|
|
|
|
8 |
14.7597 |
1.2403 |
0.7611 |
|
|
|
|
|
上記分析結果から重回帰分析の結果を検討するようにする。
2.9.2 標準偏回帰係数を求める
分析するデータを標準化して、その標準化されたデータについて回帰分析を実施すると、標準偏回帰係数を求めることができる。
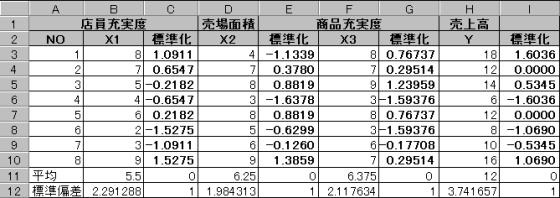
(1)分析するデータを標準化する。
![]()
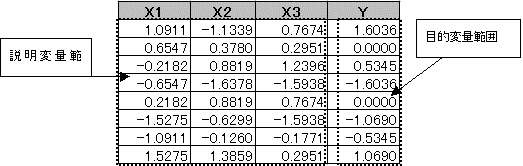
(2)標準化されたデータのみ、値複写で新しい表を作成する。
元の表で標準化されたデータを、形式指定複写の値複写で標準化データのみの新しい表を作成する。
(3)標準化されたデータの表を使用して、回帰分析を実施
|
概要 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
重相関 R |
0.91326 |
|
|
|
|
|
|
|
|
重決定 R2 |
0.83405 |
|
|
|
|
|
|
|
|
補正 R2 |
0.70958 |
|
|
|
|
|
|
|
|
標準誤差 |
0.57611 |
|
|
|
|
|
|
|
|
観測数 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
分散分析表 |
|
|
|
|
|
|
|
|
|
|
自由度 |
変動 |
分散 |
観測された分散比 |
有意 F |
|
|
|
|
回帰 |
3 |
6.672377 |
2.224126 |
6.701078 |
0.048686 |
|
|
|
|
残差 |
4 |
1.327623 |
0.331906 |
|
|
|
|
|
|
合計 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
係数 |
標準誤差 |
t |
P-値 |
下限 95% |
上限 95% |
下限 95.0% |
上限 95.0% |
|
切片 |
2.7E-18 |
0.203687 |
1.33E-17 |
1 |
-0.56553 |
0.565526 |
-0.56553 |
0.565526 |
|
X 値 1 |
0.49977 |
0.262668 |
1.902661 |
0.12984 |
-0.22952 |
1.229053 |
-0.22952 |
1.229053 |
|
X 値 2 |
-0.1458 |
0.262934 |
-0.5545 |
0.608777 |
-0.87582 |
0.584226 |
-0.87582 |
0.584226 |
|
X 値 3 |
0.59707 |
0.30882 |
1.933406 |
0.125324 |
-0.26035 |
1.454496 |
-0.26035 |
1.454496 |
標準化されたデータを使用して、回帰分析を実施すると標準偏回帰係数が求められる。この係数を使用すると、目的変量の値も求めることができる。標準偏回帰係数を見ると、X3の係数が最も大きく、目的変量に与える影響が一番大きい係数であることが分かる。もっとも元のデータにおいて、説明変量間の単位が同じであるから、標準偏回帰係数を求めなくても通常の偏回帰係数を見るだけで、どの説明変量が目的変量に与える影響が一番大きいかが分かる。
|
残差出力 |
|
|
|
|
|
|
|
|
|
観測値 |
予測値: Y |
|
標準残差 |
|
1 |
1.16878 |
0.434783 |
0.998353 |
|
2 |
0.44829 |
-0.44829 |
-1.02937 |
|
3 |
0.50249 |
0.032035 |
0.073559 |
|
4 |
-1.04 |
-0.56359 |
-1.29413 |
|
5 |
0.43865 |
-0.43865 |
-1.00723 |
|
6 |
-1.6232 |
0.554112 |
1.272357 |
|
7 |
-0.6327 |
0.098133 |
0.225334 |
|
8 |
0.73757 |
0.331472 |
0.761129 |
標準偏回帰係数を使用した予測式は、 Y
= 0.49977 X1 - 0.1458X2 + 0.59707X3 である。
この予測式を用いて予測値が計算されて求められる。
(4) 求められた予測値を更に標準化する。
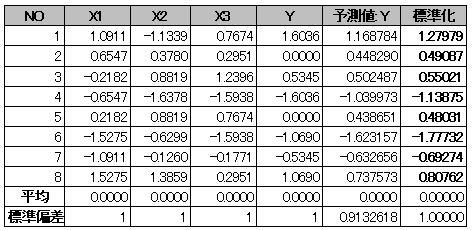
2.9.3 重回帰分析に関する関数を使用して、重回帰分析を実施
(1)各変量の係数とY切片および重回帰式の検定を実施する関数:==LINEST関数
=LINEST関数:==LINEST(既知目的変量Yの範囲、既知説明変量Xの範囲,,TRUE)
①=LINEST関数で、説明変量の商品充実度(X3変量)の係数を求める。
関数を使用するセル位置をクリックした後、関数のアイコンをクリックし、LINEST関数をクリック指定する。
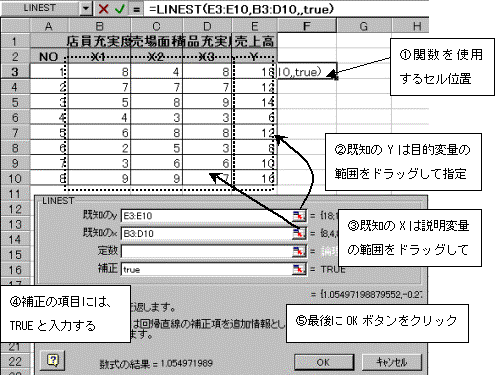
②先頭のX3の係数が求まったら、配列式を作成
現在分析に使用する説明変量は3つ、よって係数は説明変量分の3つとY切片の計4つの係数が必要であるから、配列指定は先頭のセルから横方向に4列分、また縦方向には常に5行分の範囲が必要である。よって先頭セルから横方向に4列・縦方向に5行分の範囲をドラッグして指定する。次に数式バーをクリックしアクティブにした後、CTRLキー+SHIFTキー+ENTERキーを押して配列式を完成する
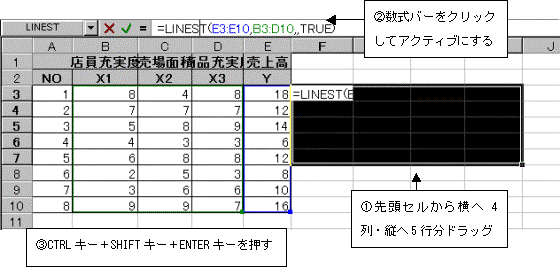
配列式が表示される
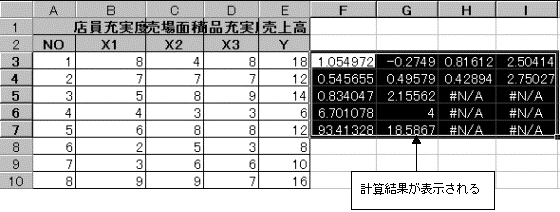
配列式に表示されているデータの意味
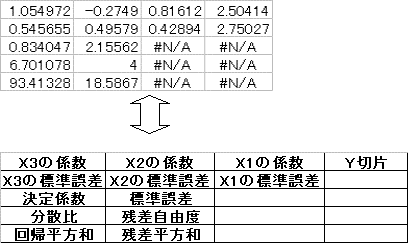
これより、重回帰式は Y=0.81612X1-0.2749X2+1.054972X3+2.50414 である。
またこの重回帰式の信頼性は、分散比(F値)=6.701078 であり、この値を使用して確率を求める関数で =FDIST(6.701078,3,4)=0.048686297 となり、求めた重回帰式は予測に役立たないという帰無仮説が棄却される。
(2)予測値を求める関数:=TREND関数
TREND関数を使用すると、重回帰式を使用して予測値を求めることができる。
TREND関数:=TREND(既知目的変量Y範囲,既知説明変量X範囲,新しいX範囲)である。
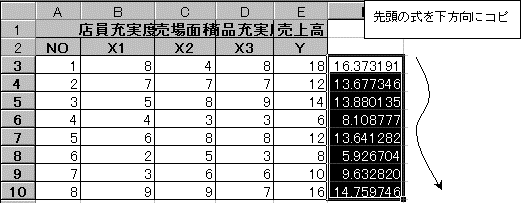
①既知目的変量Yの範囲および既知説明変量Xの範囲はドラッグして範囲指定後、F4キーを押して絶対座標にする。また新しいX範囲は、予測値を求めたいX1・X2・X3の範囲をドラッグして指定する。こちらは相対座標のままでよい。このようにして式を作成すれば、下方向にコピーして一度に予測値を求めることができる。
関数を使用するセル位置をクリックした後、関数のアイコンをクリックし、TREND関数をクリック指定する。
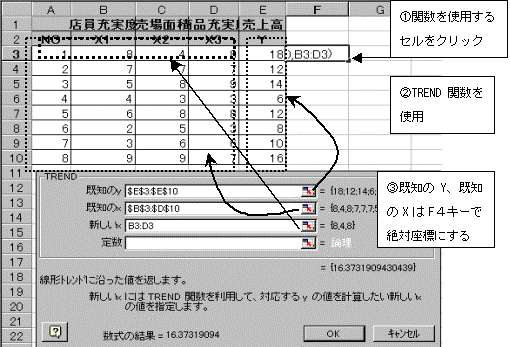
②先頭の式が作成できたら、下方向にコピーして他の予測値を求める。