�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�z�[���ɖ߂�
�P�D�U�@�W���덷�i�r�d�FStandard
Error�j
�@�W���덷�Ƃ́A����l�̕W�����i�r�c�j�������B
�@�@���܁A�W�{��1���瓾��ꂽ��A�����@�x1����11���11�{��21���21�{�c�{��p1���p1
�@�@���̕W�{��2���瓾��ꂽ��A�����@�@�x2����12���12�{��22���22�{�c�{��p2���p2
�ȉ����l�ɂ��Ă�������J��Ԃ��ƌW����1 �͐��K���z�ɏ]�����Ƃ��������Ă���B���l�ɂ�2�c��p�ɂ��Ă����ꂼ�ꐳ�K���z�ɏ]���B���̎��̕W������W���덷�Ƃ����B
1.6.1�@�W���덷�����߂�
�i�P�j�P��A�̎�
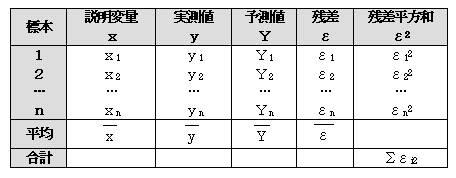
�P��A�����xi����1���i�{��0�@�Ƃ����
�c���̓�i����i�|�xi �ł��邩��A�c�������a�i�rE�j�͇���i2�����i��i�|�xi�j2
�����ϗʂ��̕������a���rXX�Ƃ���ƁA�rXX�����i��i�|���j2
�c���̕s�Ε��U�uE�́A�uE���rE�^�i���|�Q�j

�d��A�����xi����1���1i�{��2���2i�{�c�{��p���pi�{��0�@�Ƃ����
�c���̓�i����i�|�xi�ŁA�c�������a�i�rE�j��
����i2�����i��i�|�xi �j2
���R�x�́A���|���|�P
�s���U�� �uE���rE�^�i���|���|�P�j

�P�D�V�@�Ή�A�W���̌���
�W�{���瓾��ꂽ��A���̐M�����ɂ��ẮA���U���͂��s�����Ƃɂ�茟�肷�邱�Ƃ��ł���B��A�����\���ɖ𗧂Ƃ����Ƃ��A���ɕΉ�A�W�����L�����ǂ������肵�A�L���łȂ��Ή�A�W���͗\�����ʂɉe����^���Ă��Ȃ��̂ŁA�g�p���Ȃ��Ă��悢�W���Ƃ������ƂɂȂ�B
���܁A�d��A���f�����A��i����1���1i�{��2���2i�{�c�{��p���pi�{��0�{��i �ii��1,2 �c���j�Ƃ���Ƃ�
�c���Âɂ��āA
![]() �@�@��i�ƃ�j�͂��݂��ɓƗ��ł���A���K���z�@�m�i�O�C��2�j�ɏ]���B
�@�@��i�ƃ�j�͂��݂��ɓƗ��ł���A���K���z�@�m�i�O�C��2�j�ɏ]���B
�@ �A��i�̕��ϒl�i���Ғl�j�͂O�ł���B
�@ �B��i�̕��U�͈��ł���B�@
�Ƃ̉��艺�ŏd��A�\������
�xi����1���1i�{��2���2i�{�c�{��p���pi�{��0 �Ƃ���B
��Ή�A�W����i���O�����肷�邱�Ƃɂ��A���̕Ή�A�W�����\�����ʂɉe����^������W�����ǂ����̌�����s���B
1.7.1�@�P��A�ɂ������A�W������ђ萔���̌���
�@�@�P��A�����@�x����1����{��0 �Ƃ���B
�i�P�j��A�W����1�̌���
�@�@ ���蓝�v�ʂ����Ƃ����
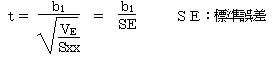
���̌��蓝�v�ʂ��͂��|�Q�̂����z�ɏ]���B
(1)����������
�@ �@ �A������ �g0�F��1���O �i�����ϗʂ��̕��A�W���͂O�ł���j
�@�@ �Η����� �g1�F��1���O �i�����ϗʂ��̕��A�W���͂O�łȂ��j
(2)���蓝�v�ʂ������߂�
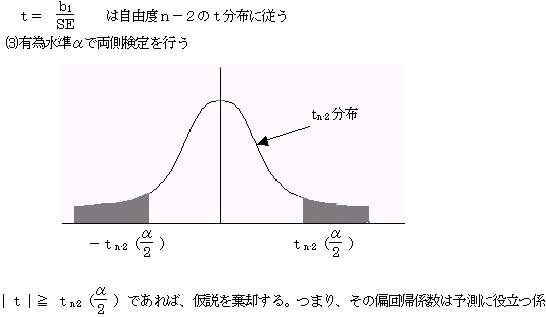
�i�Q�j�萔����0�̌���
�@�@�@���蓝�v�ʂ��́A���R�x���|�Q�̂����z�ɏ]��
�@�@�@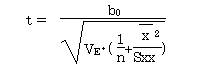
(1)����������
�@ �A������
�g0�F��0���O
�@ ������
�g1�F��0���O
(2)���蓝�v�ʂ��́A���R�x���|�Q�̂����z�ɏ]��
(3)�L�א������ŗ���������s��
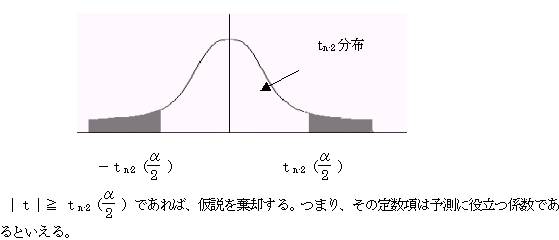
1.7.2�@�d��A�ɂ�����Ή�A�W������ђ萔���̌���
�@�@�@�d��A�����xi����1���1i�{��2���2i�{�c�{��p���pi�{��0 �Ƃ���
�i�T�j�Ή�A�W����i�̌���
���蓝�v�ʂ����Ƃ���
�@�@ 
�@�������A�r�d�F�Ή�A�W����i�̕W���덷
(1)����������
�A������
�g0�F��i���O�@�i�����ϗʂ�i�͗\���ɖ𗧂��Ȃ��j
������
�g1�F��i���O�@�i�����ϗʂ�i�͗\���ɖ𗧂j
(2)���蓝�v�ʂ��͎��R�x���|���|�P�̂����z�ɏ]��
![]()
(3)�L�א������ŗ���������s��
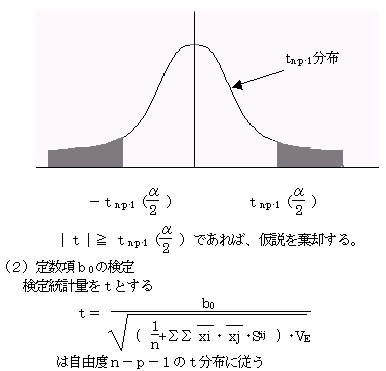
(1)����������
�A������ �g0�F��0���O�@�i�萔���͗\���ɖ𗧂��Ȃ��j
�Η����� �g1�F��0���O�@�i�萔���͗\���ɖ𗧂j
(2)���蓝�v�ʂ��͎��R�x���|���|�P�̂����z�ɏ]��
(3)�L�א������ŗ���������s��
�P�D�W�@���d�������ɂ���
�����ϗʊԂɂ����Ă��݂��ɍ������ւ����鎞�A�Ή�A�W�������߂邱�Ƃ��ł��Ȃ��Ƃ������ۂ������N�����B����𑽏d�������Ƃ����B�����ϗʊԂł��݂��ɍ������ւ�����Ƃ������Ƃ́A�ǂ�����������Ƃ�������Ă���ϐ��Ȃ̂łǂ��炩����̕ϗʂ�����悢�B�d��A�������߂�ɂ�����A���d������������Ƃ��ɂ͂ǂ��炩�̐����ϗʂ𗎂Ƃ��ċ��߂�K�v������B�@
���d�������̗L���ɂ��ẮA
(1)�����ϗʊԂ̒P���W�������߁A�P���W�����P�܂��́|�P�ɋ߂����̂�����Α��d ������������B
(2)���d���������F�߂���Ƃ��ɂ́A�Ή�A�W�������߂��Ȃ��Ƃ��A�Ή�A�W���̕����ƁA�����ϗʂƖړI�ϗʂ̒P���W���̕�������v���Ȃ����̌��ۂ��N�����B
���d�������̗�(1)
�@�@�@�@�@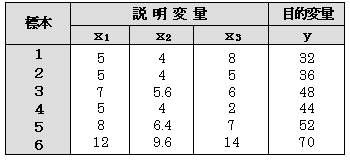
��L�\����A�����ϗʊԂ̑��֍s����쐬�����
�@�@�@�@�@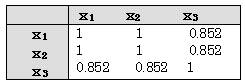
��1�|��2�̑��W�����P�ł���A�Ή�A�W�������߂邱�Ƃ��ł��Ȃ��B
�@ ��2����1�~0.8 �ƂȂ��Ă���A��2�ϗʂ͖ړI�ϗʂ��ɉ��̊�^�����Ă��Ȃ��̂ŕs�p�ȕϗʂł���Ƃ�����B��1�ϗʂ��g���Ƃ��A��2�ϗʂ𗎂Ƃ��ĉ�A�������߂Ȃ���Ȃ�Ȃ��B
�P�D�X�@�ǂ��d��A�����쐬����
�@�d��A���́A�������̐����ϗʂ���ړI�ϗʂ̒l��\�����邪�A�����ϗʂ��ނ�݂ɑ������Ă����ʂȂ��Ƃ������B���z�I�ȏd��A���́A�Ȃ�ׂ����Ȃ������ϗʂłȂ����덷�̏����ȖړI�ϗʂ���悤�Ȏ��ł���B���̂��߂ɂ͐����ϗʂׁA��A���ɕK�v�ȕϗʂł��邩����������K�v������B
�i�P�j�����ϗʂ̑I���
(1)�ړI�ϗʂɗ^����e���̑傫�������ϗʂ�I�ԁB�e�����ϗʂƖړI�ϗʊԂ̒P���W�������߂āA�e�����ϗʂ̖ړI�ϐ��ɗ^����e���̑傫���ׂ�B
(2)�����ϗʊԂō������ւ��F�߂���Ƃ��ɂ́A�ǂ��炩����̕ϗʂ𗎂Ƃ��ďd��A�����쐬����B��ʂɐ����ϗʊԂ̒P���W�����O�D�X�ȏ゠�鎞�ɂ͂ǂ��炩����̐����ϗʂ𗎂Ƃ��B���ɐ����ϗʊԂŒP���W�����P�̎��ɂ͕Ή�A�W�������߂邱�Ƃ��ł��Ȃ��B
(3)�Ή�A�W�����O�ƂȂ�悤�Ȑ����ϗʂ́A���ɂ����Ȃ��ϗʂł��邩�痎�Ƃ��悤�ɂ��B
�i�Q�j�d��A���̗ǂ���]��������@
�@�������̐����ϗʂ��g�p���ĉ���ނ��̏d��A�����쐬�����Ƃ��A�����̏d��A���̒��ŁA�ǂ̏d��A������Ԃ悢��A���ł��邩�f�����Ƃ��Ă`�h�b�i�Ԓr�̏��ʊ�j������B�`�h�b��
![]()
�ŗ^������B
�@�A�����F�W�{���@���F�����ϗʂ̌��@�rE�i�c�������a�j�F���i��i�|�xi�j2
�@�`�h�b�̒l�͏������قǓ��Ă͂܂肪�悢�Ƃ���Ă��邪�A��ΓI���^������̂ł͂Ȃ��̂ŁA�ǂ̒l�ȉ����ǂ��Ƃ͂����Ȃ��B�����܂ł́A�������̐����ϗʂ�g�ݍ��킹�č쐬������A���̂��ꂼ��̂`�h�b�l�����߁A�����̉�A���̒��ł`�h�b�l���ł����������̂���ԗǂ���A���ł���Ɣ��f����B
�P�D�P�O�@�ϐ��I��@
�@�����ϗʂ����������鎞�A�ǂ̕ϗʂ��g�p����ŗǂ̏d��A���邱�Ƃ��ł��邩���������邽�߂ɁA�ϐ��I��@������B
�i�P�j��������@
�@�����ϗʂ��o����Ƃ��A���̂o�̑S�Ă̑g�����i�QP�|�P�ʂ�j�ɂ��ĉ�A�����쐬���A��A���̌���������@�B���̕��@�ł͐����ϗʂ̌���������ƍ쐬�����A�����c��ɂȂ�A���p�I�ł͂Ȃ��B
�i�Q�j�����I��@�i�X�e�b�v���C�Y�@�j
�@�ϐ������@�c�ϐ��O����o�����A�����ϐ��𑝂₵�Ă������@
�A�ϐ������@�c�S�����ϗʎg�p������A������o�����A�����ϐ������������Ă������@
�@�B�ϐ������@�c�ϐ��O����o�����A�����ϐ��𑝂₵�Ă������A��x��荞�ϐ��ł����������Ȃ��Ȃ����Ƃ��ɂ͗��Ƃ��Ă��܂����@
�C�ϐ������@�c�S�����ϗʎg�p������A������o�����A�����ϐ������������Ă������A��x���Ƃ����ϗʂɂ��Ă����������Ƃ��ɂ͍ēx�̗p������@
�m�Ή�A�W���̂e�l���g�p�����X�e�b�v���C�Y�@�n
�i�P�j�ϐ������@
�@�@�ϐ��O����o������B
�@�A�ړI�ϗʂ��Ɗe�����ϗʂ�1�c��p�Ƃ̒P���W�������߁A���̒��ōł����W���̑傫���ϐ�����荞�ށB
�܂��́A�P���W�������߂����ɁA���|��1�@�c�@���|��p�ƂQ�ϗʂ��̉�A�����쐬���A���ꂼ��̕Ή�A�W�����݂āA���̂e�l���ł��傫���A�Ȃ����e�l���Q�ȏ�i���R�x�ɊW�Ȃ��j�̕ϐ�����荞�ށB�Ȃ��A�S�Ή�A�W���̂e�l���Q�ȉ��̎��ɂ͎�荞�ނׂ��ϐ��͂Ȃ��Ƃ���B
���܁A��1���̗p����Ƃ���Ƃx����1���1�{��0�̎����ł���B
�B���ɇA�ō̗p�����ϗʈȊO�̕ϗʂ��P�lj����ĉ�A�����쐬����B
�@���ꂼ��̉�A���ɂ��āA���̕Ή�A�W���̂e�l�����߁A�ő�̂e�l��^�������R�x�ɊW�Ȃ����̒l���Q�ȏ�̂��̂�����A�Q�Ԗڂ̕ϗʂƂ��č̗p����B
�ȉ��S�ϗʂɂ��Ă�����J��Ԃ����s����B
��^���q2 �����ꂼ�ꋁ�߂Ċ�^�����ł��傫�����̂��̗p���Ă��悢���A��^���́A�g�p����ϗʂ̌���������ƒP���ɑ�������X��������̂ŁA��^�����]����サ�ȁ@�@�@�@���Ƃ��ɂ͍̗p���Ȃ������悢�B
�C�ϐ������̑ł���
�@�S�Ă̕ϐ��ɂ��Ď��s���I�����A������荞�ނׂ��ϗʂ��Ȃ��Ȃ����Ƃ��B
�@�܂��́A�ŏ��Ɍ��߂��ł���̌���l�i�q2�j�ȉ��ɂȂ����Ƃ��B
�i�Q�j�ϐ������@
�@�ŏ��S�Ă̐����ϗʂ��g�p������A�����쐬���A���ꂼ��̕Ή�A�W���̂e�l�����߁A�ŏ��̂e�l�łȂ����Q�D�O�ȉ��̂��̂�����A���̕ϗʂ��폜����B
�A�@����P�ϗʂ����炵����A�����쐬���A���ꂼ��̕Ή�A���̂e�l�����߁A�ŏ��̂e�l�łȂ����Q�D�O�ȉ��̂��̂�����A���̕ϗʂ��폜����B������J��Ԃ��B
�@
�܂��́A��^���q2�����Ă����A���̕ϗʂ��폜���Ă��]���^���̌������݂��Ȃ��Ƃ��ɂ́A���̕ϗʂ͂Ȃ��Ă��悢�ϗʂȂ̂ō폜����B
�B�ϐ������̑ł���
�@ �S�Ă̕ϗʂɂ��Ď��s���I�����A�����폜���ׂ��ϗʂ��Ȃ��Ȃ����Ƃ��B
�@�@�܂��́A���炩���ߌ��߂�����l�i�q2�j�ɒB�����Ƃ��B
�i�R�j�ϐ������@
�@�@�@�ϐ������@�Ǝ��Ă��邪�A��x��荞�ϐ��ɂ��Ă��A���̕Ή�A�W���̂e�l���Q�D�O�ȉ��ɂȂ�Ƃ��ɂ́A��A������폜����B
�i�S�j�ϐ������@
�ϐ������@�Ɏ��Ă��邪�A��x�폜�����ϐ��ɂ��Ă��A�ēx��荞��ł��̕Ή�A�W���ׂ��̒l���Q�D�O�ȏ�ɂȂ�Ƃ��ɂ͍ēx��荞�ނ悤�ɂ���B
�ȏ�Ή�A�W���ׂĕϗʂ̑����������s���Ă������A�`�h�b�ʂ����Ȃ���ϗʂ̑��������Ă������@������B
�Ή�A�W���̂e�l�Ɠ��l�ɁA�`�h�b�ʂׂȂ���A�@�ϐ������@�@�A�ϐ������@�@�B�ϐ������@�@�C�ϐ������@�@������B
�@�`�h�b�ʂ����Ȃ��炱���̕��@���s���Ƃ��ɂ́A�̔ۂ̊�Ƃ���Ή�A�W���̂e�l�́A
�@�@���R�x�ɊW�Ȃ�
![]()
���F�W�{���@���F�����ϗʂ̌�
�P�D�P�P�@�c���Âɂ���
�@��A���ɂ����āA�c���Â��݂��
�@�c���Âɂ��Ẳ����
![]() �@�@�@�@��i���j �͂��݂��ɓƗ��ŁA���K���z�m�i�O�C��2�j�ɏ]���B
�@�@�@�@��i���j �͂��݂��ɓƗ��ŁA���K���z�m�i�O�C��2�j�ɏ]���B
�@�@�@�A�Â̊��Ғl�͂O�ł���B
�@�B�Â̕��U�͈��ł���B
�@�@�ȏ�̉��艺�Ő��`�d��A���f����
�@�@�@�@��i����1���1i�{��2���2i�{�c�{��p���pi�{��0�{��i �ii��1,2 �c���j�Ƃ���Ƃ�
�@�c���Â̕��z�́A�����_���ł��肩���K���z�ɂ��������B
���܁A�f�[�^���n���I�ɕω�����Ƃ��A�c���Â͌n���I�ɕω�����B���̎c���̌n���I�ω������邱�Ƃɂ��A�c���Ẫ����_�����ׂ邱�Ƃ��ł���B
�@�c���Ẫ����_�����ׂ�ɂ́A���̂Q�̕��@������B
�@�@�@�c���̌n���I�v���b�g�}���쐬���A���̐}����ǂݎ����@
�@�@�A�_�[�r������g�\��������ߒ��ׂ���@
1.11.1�@�c���v���b�g��������@
�@�@�f�[�^���n���I�ɕω����Ă���Ƃ��A���̉�A�������߁A��A������̂���ł���Â����n��ɕ\������B
�@�c�����݂āA�S�̓I�X���E�{�|�̏o���E�A�̒����Ɛ����ׁA�����_��������������B
�c���Ẫv���b�g�}
�A�c�{�f�[�^�E�|�f�[�^���A�����Č����Ƃ��A�����A�Ƃ����B
�@��̃T���v���ł̏o���́A�{���F�|�����X�F�X���P�F�P�ƂȂ��Ă���B
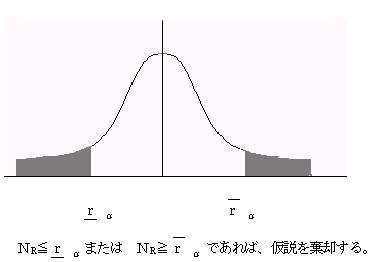
�i�P�j�c���Â̕��z���{���̕��z�Ɓ|���̕��z�����l�ɕ��z���Ă��邩�ǂ������ׂ�ɂ́A����������s���B
�c����i����i�|�xi�ł���B
�u��������̎��{�v
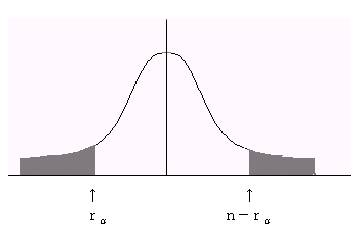
�c���Â����߂�B���̎��Á��O�̂��̂���0����A�W�{�������|��0�Ƃ���B
���蓝�v�ʂr�́{�̕����̐��Ƃ���B
(1)�W�{�������Ȃ��Ƃ��i�����R�O�j�c��������\���g�p����
�@�@����������
�@�@���@�@���@�g0�F��1����2 �i�Q�̕��z�͓������j
�@�@�Η������@�g1�F��1����2 �i�Q�̕��z�͓������Ȃ��j
�A���蓝�v�ʂr��
�@�@ �r���c���̕������{�̐�
�@�B�L�א��������ŗ���������s���i��������\������E���������߂�j
�@�@�@�@�@
�r������
�܂��́@�r���i���|�����j �Ȃ�Ή����g0�����p����B
(2)�W�{���������Ƃ��i�����R�O�j�c�W�����K���z�\���g�p����

�i�Q�j�c���Â̕��z���A�����_���ɕ��z���Ă��邩�̌���ɂ́A�u�A�̐��v�ɂ�錟�肪����B
�c���́u���镄���v�̐������Ƃ��A�u���̕����̐��v�����Ƃ���B���{�����m�Ƃ���B
���̎��u�{�̘A�v�A�u�|�̘A�v�����킹���S�̂́u�A�̐��v���mR�Ƃ���B
�@�@�@�@�@�@�mR���u�{�̘A�̌��v�{�u�|�̘A�̌��v
(1)�W�{�������Ȃ��Ƃ��i�����Q�O�C�����Q�O�j�c�A�̐��̌���\�g�p����B
�@����������
�@ ���@�@���@�g0�F�c���Â̕��z�̓����_���ł���
�@ �Η������@�g1�F�c���Â̕��z�̓����_���łȂ�
�A���蓝�v�ʂmR�͑S�̘̂A�̐��ł���
�B�L�א������Ō�����s���i�A�̐��̌���\�������E���������߂�j
�@�@�@
�@�܂�c���Â̕��z�́A�����_���łȂ��Ƃ���B
(2)�W�{���������Ƃ��i�����Q�O�C�����Q�O�j�c�W�����K���z�\���g�p����B
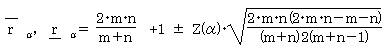 �@
�@
�@ �Ƃ��āA������s���B�Ȃ��y�i���j�́A�W�����K���z�\�̒l�ł���B
1.11.2�@�_�[�r���E���g�\�����p������@
�@�@�c���̘A�Ȃ肪�����_���ł��邩�ǂ��������肷��ɂ́A�_�[�r���E���g�\�����p������@������B�_�[�r���E���g�\��������Ƃ����
�@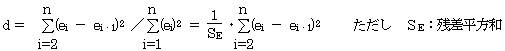
�_�[�r���E���g�\����ƃ����_�����Ƃ̊W��
�@�c�����S�������_���ł��鎞�c�����Q
�@�A�c���ɐ��̎��ȑ��ւ����鎞�c�����O�ɋ߂Â�
�@�B�c���ɕ��̎��ȑ��ւ����鎞�c�����S�ɋ߂Â�
�Ƃ��������������Ă���B
���ȑ��ւƂ́A�n���I�c���ω��Ԃ̑��ւ�����
�c���Â̎��ȑ��ւ����肷��
�i�P�j���̎��ȑ��ւ����邩�@
(1)����
�A������
�g0�F�ρ��O�@�i���ȑ��ւ͂Ȃ��j
�@�@�Η������@�g1�F�ρ��O
�i���̎��ȑ��ւ�����j
(2)���蓝�v�ʂ͂���ł���B
(3)�L�א������Ō�����s��
�@�@�@�@ ������L�Ȃ�A�����g0�F�ρ��O�����p����B�ρ��O���̑��B
�@�@�@�@�@�@������U�Ȃ�A�����g1�F�ρ��O���̑�����B
��U��������L�Ȃ�A�ρ��O�@�ρ��O�̂ǂ���Ƃ������Ȃ��B
�i�Q�j���̎��ȑ��ւ����邩
�@�@���̎��ȑ��ւ����肷��Ƃ��ɂ́A���̑���ɂS�|���Ƃ��Č�����s���B
�@(1)����
�A������
�g0�F�ρ��O�@�i���ȑ��ւ͂Ȃ��j
�@�@�@�Η������@�g1�F�ρ��O
�i���̎��ȑ��ւ�����j
(2)���蓝�v�ʂ͂���ł���B
�@ (3)�L�א������Ō�����s��
�@�@ �����S�|��L�Ȃ�A�����g0�F�ρ��O�����p����B�ρ��O���̑��B
�@�@ �����S�|��U�Ȃ�A�����g1�F�ρ��O���̑�����B
�S�|��U�������S�|��L�Ȃ�A�ρ��O�@�ρ��O�̂ǂ���Ƃ������Ȃ��B
�i�R�j���E���ǂ��炩�s���̎�
(1)����
�A������
�g0�F�ρ��O�@�i���ȑ��ւ͂Ȃ��j
�@�@�Η������@�g1�F�ρ��O �i���ȑ��ւ͂Ȃ��j
(2)���蓝�v�ʂ͂���ł���B
�@ (3)�L�א������Ō�����s��
�@�@������L�܂��͂����S�|��L�Ȃ牼���ρ��O�����p����B�i�ρ��O���̑��j
��U�������S�|��U�Ȃ牼���ρ��O���̑�����B
���̑��͕s��