�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�z�[���ɖ߂�
�P�D��A����
�@�������̑̏d�Ɛg���̒l���������Ă���Ƃ��A�̏d�̒l�͕������Ă��邪�A�g�����s���̐l������Ƃ���B���̂悤�ȂƂ��A���łɓ��Ă���f�[�^����g���Ƒ̏d�̊W�ׁA���̑��ւ����߁A�g���s���̐l�̐g����\������B���̗l�ȕ��͕��@����A���͂Ƃ����B
���߂���̂͐g���ł���A�����ړI�ϗʂƌĂԁB�g���̒l��\������̂́A�̏d����ł���̂ŁA���̑̏d�̂��Ƃ�����ϗʂƌĂԁB�����ϗʂ��P�̎���P��A���͂Ƃ����A�����ϗʂ��Q�ȏ�̎��𑽏d��A���͂Ƃ����B
��A���͂ł́A�����ϗʂ͗ʓI�f�[�^�ł���A�܂��ړI�ϗʂ��ʓI�f�[�^�ł���B
�Ȃ��A��A���ŗ\��������Ƃ��ɂ́A�����ϗʂ͈͓̔��ŗ\�����邱�Ƃ��]�܂����B�����ϗʂ͈̔͂�傫���z�����Ƃ���ŗ\������ƌ덷���傫���Ȃ���p�ɓK���Ȃ��Ȃ�B
�P�D�P�@�P��A����
�@���K��W�c���璊�o���ē���ꂽ�W�{�f�[�^���E�������\�̂悤�ɂ���A���E���Ԃɂ���W��������̂Ƃ���B
|
�W�@�{ |
�����ϗʂ� |
�ړI�ϗʂ� |
|
�P �Q �c �� |
��1 ��2 �c ��n |
��1 ��2 �c ��n |
�ȏ�̕W�{�f�[�^���w�x�O���t�ŕ`�����āA���̂悤�ɂȂ����Ƃ���
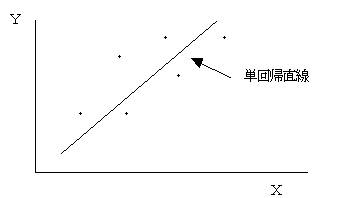
�W�{�f�[�^���E���̊Ԃɂ͉E�オ��̊W�����肻���Ȃ̂ŁA���Ƃ��̊W��\���K���Ȓ������l����B �ړI�ϗʂ��Ɛ����ϗʂ��Ƃ̊Ԃɑ��ւ�����Ƃ��A
�@�x����1����{��0�@�Ȃ钼�����P�{�l���A���f�[�^�Ƃ��̒�����̒l�Ƃ̍����ÂƂ���B

�x����1����{��0�@�Ȃ钼���͑S�Ă̕W�{�f�[�^�ɂ��āA���̎c�����ŏ��ɂȂ�悤�ɂЂ��K�v������B���̒�������e�W�{�f�[�^�Ƃ̃Y��������v�邽�߂ɁA�e�c���̕����a���Ƃ�A���̕����a���ŏ��ɂ���悤�ɂ���B���̂悤�ȕ��@���ŏ��Q��@�Ƃ����B
�@�W�{�f�[�^�́A�����x����1����{��0 ����c���i�Áj������Ă���̂ŁA�W�{�f�[�^��
������1����{��0 �{�Âƕ\���B
�@���̂��Ƃ�����`��A���f����
�@��i����1���i�{��0�{��i�@�ii��1,2�c���j�Ƃ����
�c���Âɂ��āA
![]() �@�@�@��i�ƃ�j�͂��݂��ɓƗ��ł���A���K���z�@�m�i�O�C��2�j�ɏ]���B
�@�@�@��i�ƃ�j�͂��݂��ɓƗ��ł���A���K���z�@�m�i�O�C��2�j�ɏ]���B
�@�@�A��i�̕��ϒl�i���Ғl�j�͂O�ł���B
�@�@�B��i�̕��U�͈��ł���B�@
���̂悤�ȉ��艺�ŒP��A���� �x����1����{��0 �Ƃ���B
���܁A�c���Âɒ��ڂ���Ɓ@��i����i�|�xi�@��i����i�|��1���i�|��0�@�ł���B
���̎c����S�Ă̕W�{�f�[�^�ɂ��č��v���A���̍��v�l���ŏ��ɂ���悤�Ȃ�0�E��1 �����߁A���̒P��A����B
����i2 �����i��i�|��1���i�|��0�j2 �ł��邩��
�@�������i��i�|��1���i�|��0�j2�Ƃ����
���̎�����0�C��1�ŕΔ������āA�O�Ƃ������Ƃɂ��A���K�������āA�������ŏ� �ɂ��邂0�E��1�邱�Ƃ��ł���B


�P�D�Q�@�d��A����
����ł͎��ɐ����ϗʂ���1���2�̂Q�ϗʂɂȂ����Ƃ��̉�A�������߂�B
|
�W�@�{ |
�����ϗʂ�1 |
�����ϗʂ�2 |
�ړI�ϗʂ� |
|
�P �Q �c �� |
��11 ��12 �c ��1n |
��21 ��22 �c ��2n |
��1 ��2 �c ��n |
�����ϗʂ��Q�ϗʂ���̂ŁA�P���ɐ����Q�ϗʁi��1�Ƃ�2�j�̕��ϒl���Ƃ��āA���̒l�ƖړI�ϗʁi���j�Ƃ̑��ւ����߂Ă��A���ϒl���Ƃ�i�K�Ŏ������ʂ��傫���̂Ő�������A���邱�Ƃ��ł��Ȃ��B
���̂悤�ɐ����ϗʂ��Q�ȏ゠�鎞�̉�A���͂��d��A���͂Ƃ����B
1.2.1�@�d��A�������߂�B
�@�Q�����ϗʂ����̂悤�ɂȂ��Ă���Ƃ��̏d��A���������߂�B
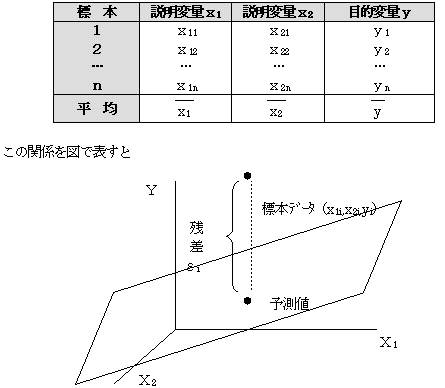
�����ϗʁi��1�C��2�j�ƖړI�ϗʁi���j�Ƃ̊Ԃɑ��֊W������Ƃ�
�@�@�@�@�x����1���1�{��2���2�{��0
�Ȃ镽�ʂ��l���A���ۂ̕W�{�f�[�^���炱�̂��̕��ʏ�ւ̎c�����ÂƂ����
�����ϗʂ��Q���鎞�̏d��A����
�@�@�@�@��i����1���1i�{��2���2i�{��0�{��i�@�ƕ\�����B
�c���Âɒ��ڂ���� ��i����i�|�xi
��i����i�|�i��1���1i�{��2���2i�{��0�j�ł��邩��
���̎c�������a�����߁A�c�������a���ŏ��ɂ���悤�Ȃ�0�E��1�E��2 �����߂�ƁA�d��A���邱�Ƃ��ł���B
��ʂɐ����ϗʂ������鎞�̐��`�d��A���f����
�@�@�@�@��i����1���1i�{��2���2i�{�c�{��p���pi�{��0�{��i �ii��1,2 �c���j
�ƕ\�����B���̎��P��A���͂Ɠ��l��
�c���Âɂ��āA
![]() �@�@�@��i�ƃ�j�͂��݂��ɓƗ��ł���A���K���z�@�m�i�O�C��2�j�ɏ]���B
�@�@�@��i�ƃ�j�͂��݂��ɓƗ��ł���A���K���z�@�m�i�O�C��2�j�ɏ]���B
�@�@�A��i�̕��ϒl�i���Ғl�j�͂O�ł���B
�@�@�B��i�̕��U�͈��ł���B�@
�Ƃ̉��艺�ŏd��A�\������
�@�xi����1���1i�{��2���2i�{�c�{��p���pi�{��0 �Ƃ���B
�@��1���2�c��p��Ή�A�W���Ƃ����A ��1���2�c��p ���Ή�A�W���Ƃ����B
�m�c�������a���i��i�j2 ���ŏ��ɂ���悤�Ȃ�0���1���2 �����߂�B�n
���i��i�j2 �����o��i�|�i��1���1i�{��2���2i�{��0�j�p2 ���ŏ��ɂ��邂0���1���2 ��
���߂�B
�������i��i�|��1���1i�|��2���2i�|��0�j2 �Ƃ��A���̎�����0���1���2�ŕΔ�������B

1.2.2�@�������a�E�Ϙa����d��A�������߂�
�@(1)�����ϗʂ��Q�̎�
�����ϗʂ�1���2 �̕������a���ꂼ��r11�E�r22�A���Ϙa���r12�Ƃ����

���߂�d��A�����A�xi����1���1i�{��2���2i�{�c�{��p���pi�{��0 �Ƃ���A���̉�A���̌W����0�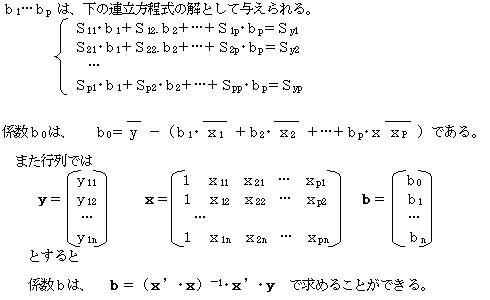
�P�D�R�@�W���Ή�A�W��
�@�����ϗʂ��ǂꂭ�炢�ړI�ϗʂɉe����^���Ă��邩�i��^���Ă��邩�j������ɂ́A���߂��d��A���̕Ή�A�W��������悢�B�ʏ�A�Ή�A�W�����傫���قǖړI�ϗʂɗ^����e�����傫���̂ő�����^���Ă���Ƃ�����B�������A�����ϗʊԂŒP�ʂ��قȂ�Ƃ��ɂ́A�P�ʂ̉e������̂ŁA�P���ɕΉ�A�W���̑召��r���Č��߂邱�Ƃ͂ł��Ȃ��B�P�ʂ̉e���������ɂ́A�W�{�f�[�^��W��������B�f�[�^��W�������邱�Ƃɂ��A���ρ��O�E���U���P�ƂȂ�P�ʂ̉e�����Ȃ��Ȃ�̂ŁA�W���������f�[�^����Ή�A �W�������߂�悤�ɂ���B���̂悤�ɕW���������f�[�^���瓾��ꂽ�Ή�A�W�����A�W�� �Ή�A�W���Ƃ����B
�W���Ή�A�W���̑傫���قǁA�ړI�ϗʂɗ^����e�����傫���A��^�̑傫���ϗʂł��� �Ƃ�����B

�P�D�S�@���W���ƌ���W��
1.4.1�@�P��A���ɂ����鑊�W���ƌ���W��

�����l���́A�P��A�����̕t�߂ɂ���ĎU�݂��Ă���B���̂���̏������قǒP��@�@�A���̂��Ă͂܂肪�悢�i���x�������j�����Ƃ�����B�܂������ϗʂ��̖ړI�ϗʂɗ^����e�����傫���Ƃ�����B�܂茈��͂��傫���Ƃ�����B

�i�P�j�d���W���ƌ���W��

�m�d���W���̌���n
�W�{���瓾��ꂽ�d���W���ɂ��āA���̕�d���W���i�ρj�������ւ��ǂ����̌�����@�@�s���B�W�{���瓾��ꂽ�d���W����R�Ƃ��鎞�A���̕ꑊ�W���i�ρj�ɂ��ăρ��O�̉����ɂ��A���蓝�v�ʂ��e�Ƃ����

����������Ȃ�
�@�@(1)����������
�@�@�@ ���@�@���@�g0�F�ρ��O �i��d���W���͖����ւł���j
�@�@�@ �Η������@�g1�F�ρ��O �i��d���W���͖����ւł͂Ȃ��j
(2)���蓝�v�ʂe�͎��R�x���C���|���|�P�̂e���z�ɏ]���B
�@�@(3)�L�א������Ō�������s����B
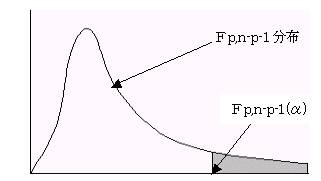
�e���ep,n�|p�|1(��)�ł���A���������p����B�܂�A��d���W���͗L���ł���A�����l�Ɨ\���l�̊Ԃɂ͑��ւ�����Ƃ�����B
�d���W���́A�����l���Ɨ\���l�x�Ƃ̑��W���ł���B����ɑ��ĒP���ɂQ�ϗʊԂ̑��W����P���W���Ƃ����B���ϗʃf�[�^�ɂ����āA�Q�ϗʊԂ̑��W�����{���ɐ��������ւ������Ƃ͌���Ȃ��B���ϗʂɂ����Ă͂Q�ϗʊԂ̑��W�������߂Ă��A���̂Q�ϗʈȊO�̕ϗʂ����̂Q�ϗʂɉe����^���邩��ł���B����āA���ϗʊԂɂ�����Q�ϗʂ̐��������W�������߂�ɂ́A���W�������߂�Q�ϗʈȊO�̕ϗʂ̉e������菜���āi���ɂ��āj���W�������߂�K�v������B���̂悤�ɂ��ċ��߂����W����Α��W���Ƃ����B
�i�Q�j�Α��W��
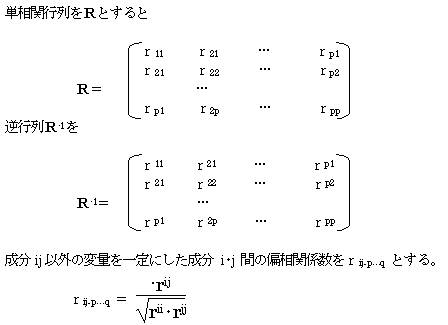
���ϗʃf�[�^�ɂ����āA�C�ӂ̂Q�ϗʊԂ̒P���ȑ��W����P���W���Ƃ������A����͑��ւ��Ƃ�Q�ϗʈȊO�̕ϗʂ��A���̂Q�ϗʂɉe����^���Ă��鑊�W���ł���B����ɑ��A���ւ����߂�Q�ϗʈȊO�̑��̕ϗʂ̉e������菜�����Q�ϗʊԂ̑��W����Α��W���Ƃ����B
���܂o�ϗʂ̔C�ӂ̂Q�ϗʊԂ̒P���W������ij�Ƃ���B
|
|
��1 ��2 �c ��p |
|
��1 ��2 �c ��p |
��11 ��21
�c ��p1 ��21 ��22
�c ��p2 �c ��p1 ��2p
�c ��pp |
�i�R�j���R�x������W��
�@����W����d���W���́A�����ϗʂ̐��𑝂₷�ƒP���ɑ�������X��������B
�����ŁA�P���ɐ����ϗʂ̐��𑝂₵�Ă��A����W�����P���ɑ������Ȃ��悤�ɒ��������@�@�@���R�x�����ς���W���Ƃ����B�ʏ�W�{�������A�����ϗʂ����|�P�̂��͕̂��͂��邱�Ƃ��ł��Ȃ��B�K�������ϗʂ����|�Q�ȉ��ɂ���K�v������B
���R�x�����ς���W�����q�f2 �Ƃ����

�P�D�T�@��A���̐M����
�@��A�����g�p���Đ����ϗʂ���ړI�ϗʂ̒l��\�����鎞�A���̗\���l���ǂ̂��炢�M�����@�@������̂������肷����@�ɁA���U���͂�p������@�Ƒ��W����p������@������B
1.5.1�@���U���͂�p����ꍇ
�i�P�j�P��A�̂Ƃ�
�@�@�@�����ϗʂ��Ǝ����l���ƒP��A�����狁�߂��\���l�x�����\�̂悤�ł��鎞
|
�W�@�{ |
�����ϗʂ� |
�����l�� |
�\���l�x |
|
�P �Q �c �� |
��1 ��2 �c ��n |
��1 ��2 �c ��n |
�x1 �x2 �c �xn |
�\���l�xi�́A�x����1����{��0�̉�A�����狁�߂��l
�ȏ�̃f�[�^�����ƂɁA���U���͕\���쐬����A���̐M���������肷��B
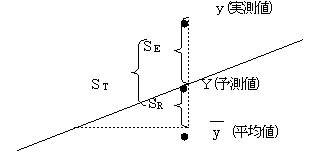
�@�S�̂̕ϓ��i�rT�j���A��A�ɂ��ϓ��i�rR�j�Ǝc���ɂ��ϓ��i�rE�j�Ƃɕ����A��A�ɂ��ϓ����c���ɂ��ϓ������������悤�ł���A��A�����ŋ��߂��\���l�͎c���ɂ��e���̕����傫���̂ŗ\���ɂ͖𗧂��Ȃ��ƍl����B
�����l�̕ϓ��i�rT�j����A�ɂ��ϓ��i�rR�j�{�c���ɂ��ϓ��i�rE�j
�@ �c�����������قǢ�����l�̕ϓ���ࢉ�A�ɂ��ϓ���ƂȂ�A�悢�\���l����B
(1)�ϓ������߂�
�@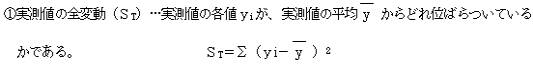

�E�Б�������s���A�uR���uE���傫�����ǂ������肷��B�uR���uE�ł���A��A�ɂ��ϓ����c���ɂ��ϓ������S�ϓ��ɗ^����e�����傫���̂ŁA��A�����͗\���ɖ𗧂Ƃ�����B
(5)������s��
�@(1)����������
���@�@��
�g0�F��A�����͗\���ɖ𗧂��Ȃ��i�uR���uE�j
������
�g1�F��A�����͗\���ɖ𗧂i�uR���uE�j
(2)���蓝�v�ʂe�����߂�
![]()
(3)�L�א������ʼnE�Б�������s��
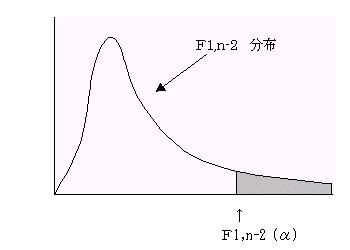
�e���e1,n-2 (��)�ł���A�����g0�����p���A�Η������g1�F��A�����͗\���ɖ𗧂��̑�����B�܂�A���̉�A�����͗\���ɖ𗧂Ƃ���B
�ȏ���܂Ƃ߂ĕ��U���͕\���쐬����B
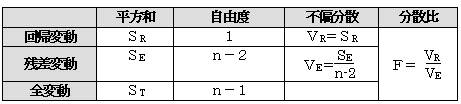
���U��e�͎��R�x�P�C���|�Q�̂e���z�ɏ]��
�i�Q�j�d��A�̂Ƃ�
�@�����ϗʂ��o���鎞�̑��ϗʃf�[�^�����̂悤�ɂȂ��Ă���Ƃ���
�\���l�͂x����1���1i�{��2���2i�{�c�{��p���pi�{��0 ���瓾���l
�@�@�@�@�@���F�W�{���@�@���F�����ϗʂ̌�
�P��A���l�ɁA�S�̂̕ϓ�����A�ɂ��ϓ��Ǝc���ɂ��ϓ��Ƃɕ����A���U���͕\����@�@�@�����d��A���̐M���������肷��B
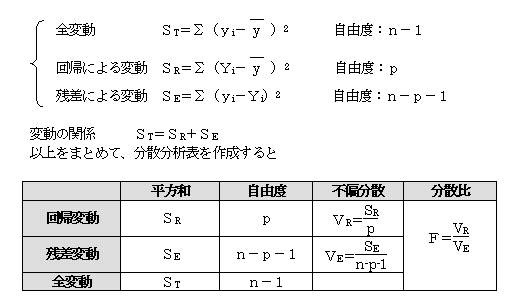
���U��e�́A���R�x���C���|���|�P�̂e���z�ɏ]���̂ŁA����𗘗p���ĒP��A�̏ꍇ�Ɠ��l�ɉ�A���̐M���������肷�邱�Ƃ��ł���B
���U���͂ł́A��A���̐M���������肷�邱�Ƃ͂ł��邪�A�ǂ�ʐM���ł��邩�ɂ��ā@�@�@�͕s���ł���B
1.5.2�@���W����p����ꍇ
�@���W��R�̂Q��͌���W���ƌĂ�Ă��邪�A���̌���W���𗘗p���ĉ�A���̐M�����@�@�@������B
