�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�z�[���ɖ߂�
EXCEL�ł̍s�Z
�P�D�@�]�u�s������߂�B
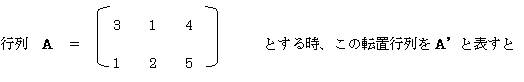
����A�f�́A�s��A�̍s�Ɨ�����ւ����s��ł���B
���ł́@��TRANSPOSE(�s��͈�)�ŋ��߂�B
���E�B�U�[�h���g�p���ċ��߂Ă��悢���A�L�[�{�[�h���璼�ړ��͂��Ă��悢�B
1.1�@���E�B�U�[�h���g�p����
�@(1)���̍s��A����͂��Ă����B
�@(2)�]�u�s������߂����擪�̃Z�����N���b�N����B
�@(3)���E�B�U�[�h��f���̃A�C�R�����N���b�N����B���E�B�U�[�h���N������̂ŁA���̒��̌���/�s����N���b�N���A����TRANSPOSE���N���b�N����B
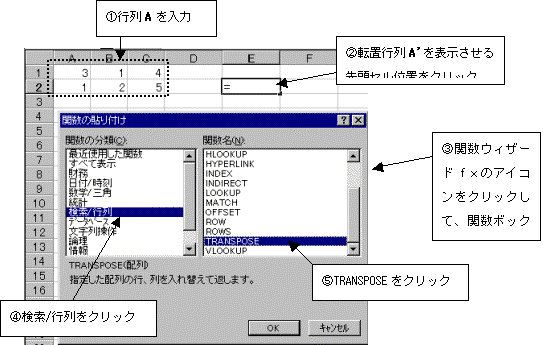
�@(4)TRANSPOSE���ŁA�]�u�s������߂����s��͈̔͂��w�肷��B
�͈͎w��ɂ́A�͈͎w��{�^�����N���b�N���A���ɔ͈͂��h���b�O���A�͈͎w��I���{�^�����N���b�N����B�Ō��OK�{�^�����N���b�N����B
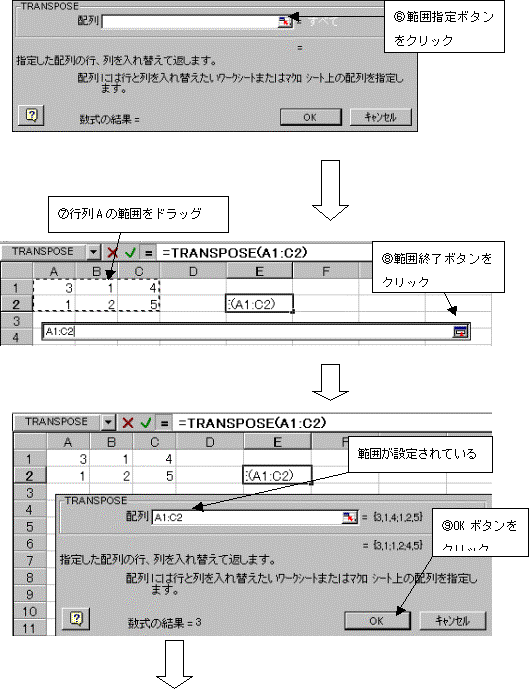
��VALUE�ƕ\������邪�A���̎���z��W�J����B
�L�[�{�[�h���璼�ڊ��F�u��TRANSPOSE(�v�Ɠ��͂��A���ɍs��A�͈̔͂��h���b�O���A�Ō�Ɂu)�v�Ɠ��͂��Ă��悢

(5)���̍s��A��2�s3��ł��邩��A���̓]�u�s��A'��3�s2��ɂȂ�B
�擪�̎����n�_�ɂ��āA3�s2�h���b�O���A���ɐ����o�[���N���b�N����B
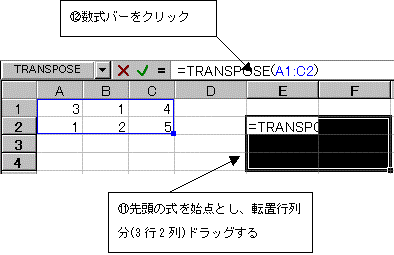
(6)CTRL�L�[�{SHIFT�L�[�{ENTER�L�[�������ēW�J�����s����B
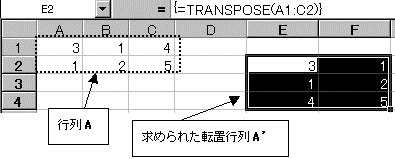
�]�u�s��́A���̍s����s�E������ւ��邾���ł��邩��A�ڂŌ��Ȃ��璼�ڐ��l����͂��Ă��悢���A�Ԉ���ē��͂��邱�Ƃ�A���̍s��̒l��ύX�������ɍēx�ڂŌ��Ȃ���������͂��Ȃ���Ȃ�Ȃ��B����TRANSPOSE�����g�p���Ă����A�ԈႢ�͂Ȃ����A���̍s��̒l��ύX����ƁA����ɉ����Ď����I�ɍČv�Z����āA�������l�ƂȂ�B
�Q�D�P�@�t�s������߂�B
�@�t�s������߂�ɂ́A���̍s�����s��(�s���E���ɓ����傫���̍s��)�łȂ���Ȃ�Ȃ��B
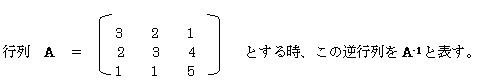
����A-1�́A��v�Z�ŋ��߂�͖̂ʓ|�ł���B
�t�s������߂���F��MINVERSE(�s��͈�)���g�p����ΊȒP�ɋ��߂���B������@�́A�]�u�s��̎��Ɠ������@�ōs���B
�@(1)���̍s��A����͂��Ă����B
�@(2)�t�s������߂����擪�̃Z�����N���b�N����B
�@(3)���E�B�U�[�h��f���̃A�C�R�����N���b�N����B���E�B�U�[�h���N������̂ŁA���̒��̐��w/�O�p���N���b�N���A����MINVERSE���N���b�N����B
MINVERSE���̃{�b�N�X���J���̂ŁA�͈͎w��{�^�����N���b�N���A���̍s��͈͂��h���b�O���Ďw���A�͈͎w��I���{�^�����N���b�N���A�Ō�OK�{�^�����N���b�N����B
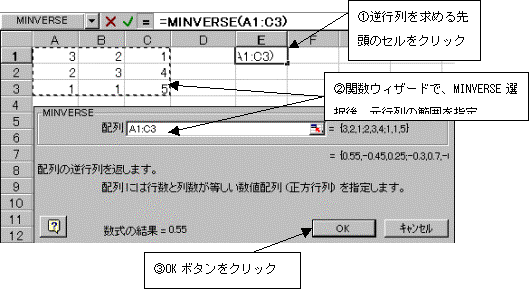
���s��A��3�s�E3��ł��邩��A�t�s���3�s�E3�K�v�ł���B�擪�̃Z���ʒu����3�s3�h���b�O���A���ɐ����o�[���N���b�N���ACTRL�L�[�{SHIFT�L�[�{ENTER�L�[�������ēW�J����B
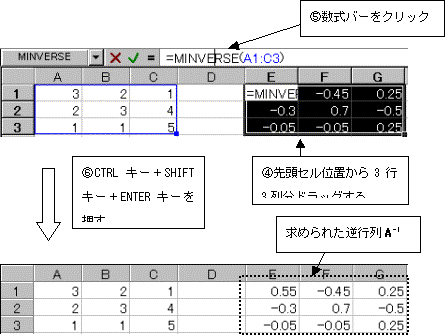
�Q�D�Q�@���Ƃ̍s�Ίp�s��ł��鎞�̋t�s������߂�B
�����s��ŁA�Ίp�����ȊO�͂��ׂ�0�̂悤�ȍs���Ίp�s��Ƃ����B���̍s��A���A���̑Ίp�s��ł��鎞�A���̋t�s��͔��ɊȒP�ƂȂ�B
���ܐ����s��ŁA�Ίp�������A1,2,3,4�ł���A���̐����͂��ׂ�0�ł���悤�ȑΊp�s��A������Ƃ���B
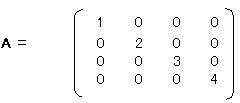
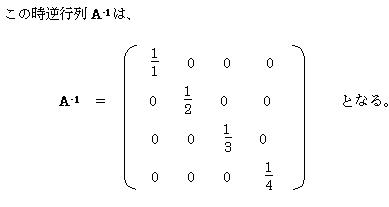
�@�@A-1/2�@���@(A1/2)�]1�@�ł��邩��AA�]1/2�����߂�ɂ́A�ŏ��Ɋe�����̕����������߁A�����Ă��̋t�s������߂�悢�B

�R�D�@�s�����߂�B
�@�����s��A�ɂ����āA���̍s�� �bA�b �����߂�B
�s�����߂���F��MDETERM(�s��͈�)���g�p����B
�����s��A����͂��Ă����B������\�����������Z���ʒu���N���b�N����B���E�B�U�[�h�̃A�C�R��fx���N���b�N���A���w��{�b�N�X���J���B���w/�O�p���N���b�N���A������MDETERM���N���b�N����B
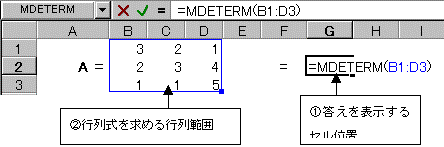 MDETERM���{�b�N�X���J���̂ŁA�s�����߂����s��͈͂��h���b�O���AOK�{�^�����N���b�N����B
MDETERM���{�b�N�X���J���̂ŁA�s�����߂����s��͈͂��h���b�O���AOK�{�^�����N���b�N����B
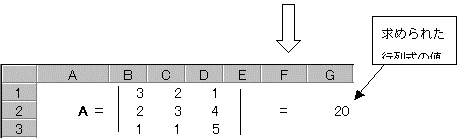
�S�D�@�s��̐ς����߂�B
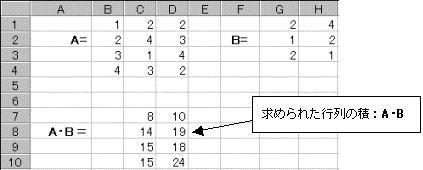
�@�s��A��l�s����A�s��B�����sn��ł���A���̍s��̐ς́A���s����ƂȂ�B
�@�s��A��4�s3��B�s��B��3�s2��ł���A�s��̐�A�B��4�s2��ƂȂ�B
2�̍s��̐ς����߂���F��MMULT(�s��1�C�s��2)�ł���B
�@�s��̐ς́A���̏��Ԃ��d�v�ł��邩��AA�B�����߂鎞�ɂ́A�s��A�͈̔͂��s��1�͈̔͂ɂ��A�s��B�͈̔͂��s��2�͈̔͂ɂ��Ȃ���Ȃ�Ȃ��B
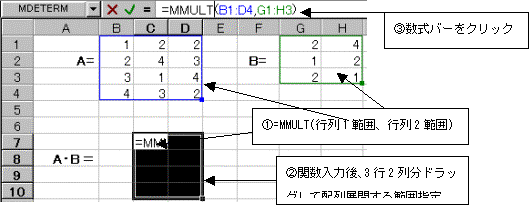
�Ō�ɐ����o�[���N���b�N������ACTRL�L�[�{SHIFT�L�[�{ENTER�L�[�Ŕz��W�J����B
�T�D�@�s����g�p���āA�A��������������
�s����g�p�����������́AA�X��B
�Ə�����ŁAX=A-1�B�ŋ��߂���B
![]() �@�@ 42 X1�{
15 X2�{ 24.5X3��56
�@�@ 42 X1�{
15 X2�{ 24.5X3��56
�@�@ 15 X1�{ 31.5 X2�{ 21.25X3��26
�@�@24.5X1�{21.25X2�{35.875X3��52
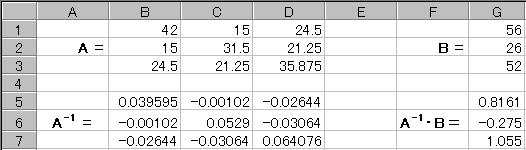
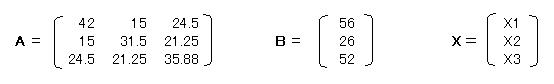 ��̕��������A�s����g�p���ĉ����B
��̕��������A�s����g�p���ĉ����B
�Ƃ���ƁAX��A�̋t�s��A-1��B�̐ςŋ��߂���B
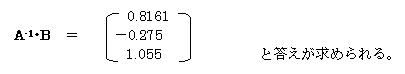
�U�D�@�ŗL�l�����߂�B�@
�@�@�听�����́E�������֕��́E���ʉ�2�ށE3�ނȂǂ̕��͂����{���鎞�ɂ́A�s�Z�ŌŗL�l�����߂Ȃ���Ȃ�Ȃ��B�ŗL�l�����߂�̂́A���R�r�@�A�ׂ���@�A�O�d�Ίp���@�Ȃǂ����邪�A����������Z���J��Ԃ����{���Ȃ���Ȃ炸�A�\�v�Z�ł��̍�Ƃ����{���邱�Ƃ͓���B
�@�\�v�Z�Ŋȕ֓I�Ɏ��{������@�Ƃ��ẮA�s���g�p���ċ��߂邱�Ƃ͂ł���B
�ŗL�l�����߂�s��m�sm��ł�����ŗL�l��m���߂���B
�@���܉��̂悤�ɁA3�s3��̍s�ŌŗL�l�ɂ����߂�B3�s3��ł��邩��A�ŗL�l�ɂ�3���߂���B
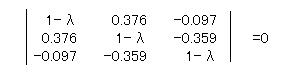
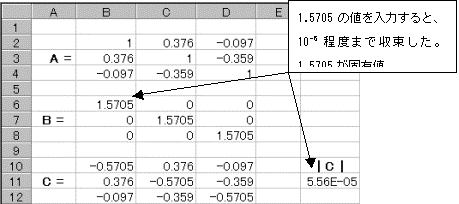
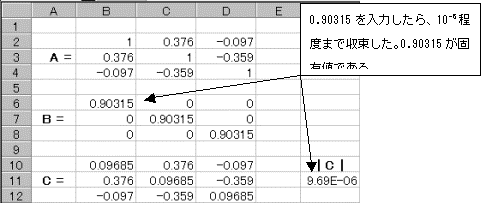
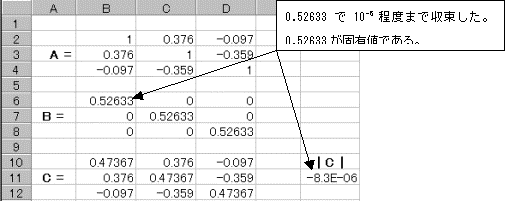
�@����������ɂ́A�ʏ�3���������������Ȃ���Ȃ�Ȃ����A�ɂ��������s��A�ƁA�Ίp�������ɂ���Ȃ�Ίp�s��B���쐬���AA�|B�̐V�����s��C���쐬����B����C�̍s�����ŋ��߂�悤�ɂ��Ă����B�ŏ��͑Ίp�s��B�̊e������0�ɂ��Ă����A�Ίp������1�s1��ڂɒl����͂���Ƒ��̑Ίp�����͂��ׂĂ��̒l�ɂȂ�悤�ɎQ�Ǝ�����͂��Ă����B
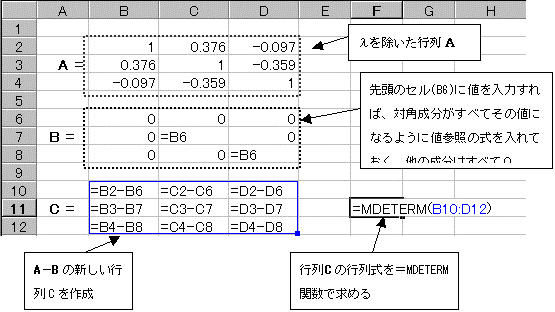

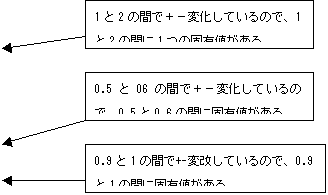
�bC�b�̒l�����Ȃ���A�Z��B6�ɏ������l����͂��Ă����Ƃ����ɍČv�Z����Ă��̌��ʂ��bC�b�ɕ\�������B�bC�b���{����|�ɕς��Ƃ���������A�bC�b��10-5���x�܂ł̒l�ƂȂ��������ŗL�l�̒l�ƂȂ�B���̓_��3����̂ł���3�_��T���Ă����B
|
|
�bC�b�̒l |
|
3 |
-7.414481 |
|
2 |
-0.694147 |
|
1 |
0.0261869 |
|
0 |
0.7465209 |
|
-1 |
7.4668549 |
|
-2 |
26.187189 |
|
0.5 |
0.0113539 |
|
0.6 |
-0.02168 |
|
0.9 |
-0.00078 |
|
1 |
0.0261869 |