�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�z�[���ɖ߂�
�S�D�@EXCEL�ɂ�锻�ʕ��͗��
�@�����Ђ�K�₵�Ă������Ђ̎Ј��i�`�ƊE�Ј��Ƃa�ƊE�Ј��j�ɂ��āA���̈�ۂɂ��āA�P�O�_�]���������̂����̕\�ł���B�`�ƊE�Ј��Ƃa�ƊE�Ј��Ԃň�ۂɈႢ�����邩�ǂ������ׂ�B
|
�m�n |
�w1 ��V |
�w2 �ϋɐ� |
�w3 ������ |
�w4 �ƊE�敪 |
|
�P �Q �R �S �T �U �V �W |
�R �W �U �W �V �S �U �V |
�W �Q �V �U �R �V �R �T |
�S �U �U �S �T �R �U �W |
�` �a �` �` �a �` �a �a |
���e�_�́A�P�O(��)�`�O(��)�@�̂P�O�_�]���l�B�ƊE�敪�͂`�ƊE�Ƃa�ƊE�̂Q��
�@��̕\�����Ƃɂ��āA���ʕ��͂����{���Ă`�ƊE�Ƃa�ƊE�̎Ј��Ԃň�ۂ��Ⴄ���ǂ������@�ׂ�B�`�ƊE���u�P�v�E�a�@�ƊE���u�Q�v�Ǝ��I�敪�f�[�^�ɒu��������B�����f�[�^���玿�I���l�f�[�^�ɒu���������f�[�^���g�p���Ĕ��ʕ��͂����s����B
|
�m�n |
�w1 ��V |
�w2 �ϋɐ� |
�w3 ������ |
�w4 �ƊE�敪 |
|
�P �Q �R �S �T �U �V �W |
�R �W �U �W �V �S �U �V |
�W �Q �V �U �R �V �R �T |
�S �U �U �S �T �R �U �W |
�P �Q �P �P �Q �P �Q �Q |
�@���ʕ��͂����{����ɂ́A�܂����͂���f�[�^����͂��āB�P�P�[�X������̕ϐ��͂w1�`�w4�ł���A�m�n�P�`�m�n�W�@�܂ł̂W�P�[�X���̃f�[�^������B���͗p�f�[�^���͌�A���ʕ��͂����{����B
�S�D�P�@���ʕ��͂̎��{
�@�{�b�N�X�l��������{���A���`���ʎ��ŋ敪���邩�A�}�n���m�r�X�̋�����p���Ĕ��ʂ��邩�����肷��B
�@�{�b�N�X�l����́A�Q�����������̂Q�Q�̕ꕪ�U�����U�����������ǂ����̌���ł���B�{�b�N�X�l����̌��ʂQ�Q�̕ꕪ�U�����U����������A�Q�Q�͐��`���ʎ��ŋ敪���邱�Ƃ��ł���B�Q�Q�̕ꕪ�U�����U���������Ȃ���}�n���m�r�X�̋����ɂ�锻�ʕ��͂����{����B
4.1.1�@�Q1�iA�ƊE�j�E�Q2�iB�ƊE�j���ꂼ��̕��U�E�����U�����߂�
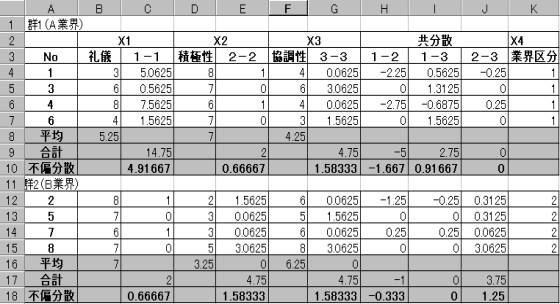
�s�Ε��U�́A�� (Xi�|
)2�@�@�@�@�s�����U�́A�� (Xi�|
)(Xj�|)
�v�[����̕��U�����U�͎�����苁�߂�B
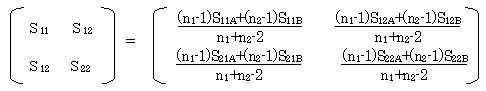
4.1.2 ���蓝�v�ʂ���2 �Ƃ��āA���̌��蓝�v�ʂ����߂�B
�Q�P�i�`�ƊE�Ј��j�̕��U�����U�s����r1�A�W�{������1�A�Q�Q�i�a�ƊE�Ј��j�̕��U�����U�s����r2�A�W�{������2�A�܂��v�[���������U�����U�s����r�A�ϗʐ������Ƃ����
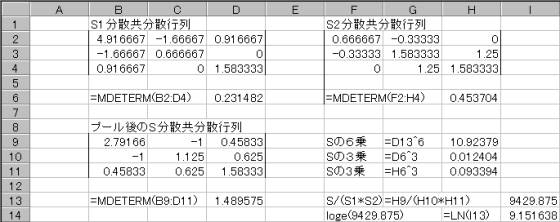
�s�̒l�́A��MDETERM(�͈́j�ŋ��߂�B�����������s��Ɍ���
�ȏ�����g�p���ċ��߂��l�������

�@�@loge(���l)�̒l�́A�����g�p����=LN(�l)�ŋ��߂�B
loge9429.875 = 9.151638
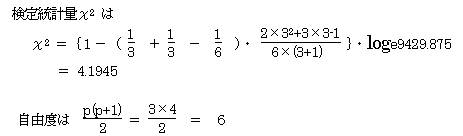
4.1.3�@��������{
�A�������F�g0 �F�Q�Q�̕ꕪ�U�����U�͓�����
�Η������F�g1 �F�Q�Q�̕ꕪ�U�����U�͓������Ȃ�
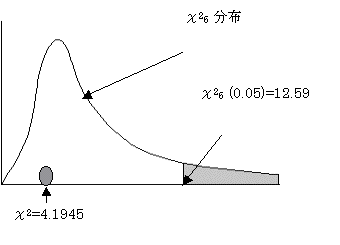
��2 �� ��26 (0.05) �ł���A���p��ɓ���Ȃ��B����ĉ����g0�F�i�Q�Q�̕ꕪ�U�����U�͓������j�����p�ł��Ȃ��B�Q�Q�̕ꕪ�U�����U�s��͓������Ȃ��Ƃ͂����Ȃ��B����ĂQ�Q���A���v���ʎ��ŕ�����B
�S�D�Q�@���`���ʎ������߂�B
4.2.1�@���U�����U�s������߂�B
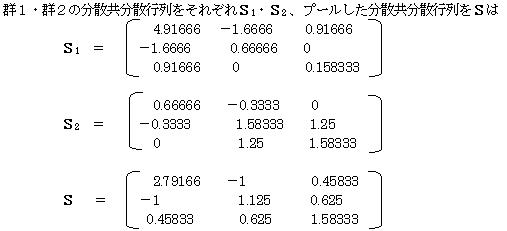
4.2.2�@�Q�P�ƌQ�Q�̊e�ϗʂ̕��ϒl�̍����Ƃ�
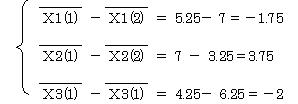
�ȏォ��
![]() 2.79166�a1 �| a2 �{ 0.45833�a3
=�|1.75
2.79166�a1 �| a2 �{ 0.45833�a3
=�|1.75
�@�@�@�|a1 �{ 1.125�a2
�{ 0.625�a3 = 3.75
0.45833�a1 �{ 0.625�a2 �{ 1.58333�a3
= �|2
�i������a1�a2�a3 �͕ϗʂw1�E�w2�E�w3 �̊e�W���j
��̌v�Z��EXCEL�̌v�Z�@�\���g�p���ċ��߂�B
�v�[����̕��U�����U�s��S�ƁA���ς̍��̍s�����͂���B
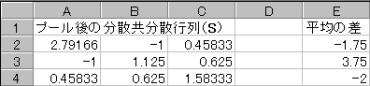
���U�����U�s��̋t�s������߂�B
�@�擪�̒l����MINVERSE(�s��͈�)�ŋ��߂�B
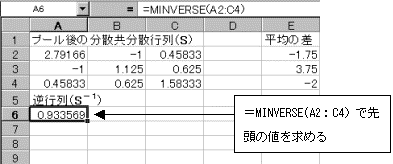
�擪�̒l�����܂�����A��������t�s������߂�͈͂��h���b�O���A���ɐ����o�[���N���b�N������ACTRL�L�[�{SHIFT�L�[�{ENTER�L�[�������āA�z����������B
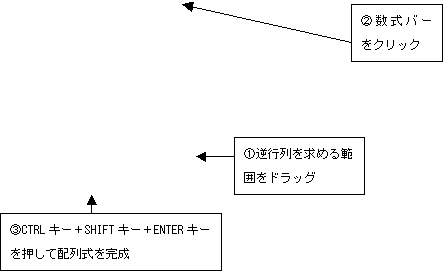
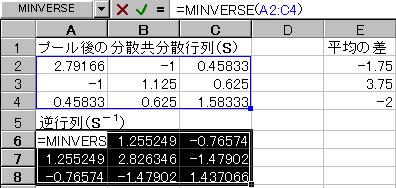
���܂���S�̋t�s��iS-1�j�ƕ��ς̍��̍s��̐ς����߂�B
�擪�̒l����MMULT(�s��1�͈́C�s��2�͈�)�ŋ��߂�B
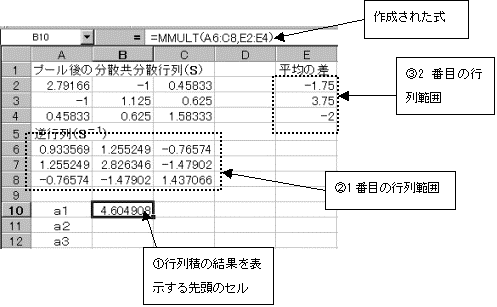
�s��ς����߂�͈͂��h���b�O������A�����o�[���N���b�N���ACTRL�L�[�{SHIFT�L�[�{ENTER�L�[�������Ĕz����������B
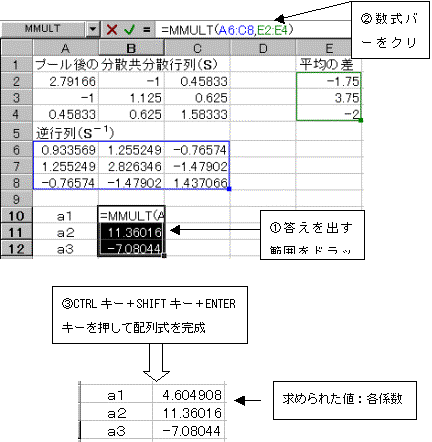
������
a1=4.605�@a2=11.36�@a3 =�|7.08
![]() ����Đ��`���ʎ��́A�x��4.605��w1�{11.36��w2�|7.08��w3�|49.25
����Đ��`���ʎ��́A�x��4.605��w1�{11.36��w2�|7.08��w3�|49.25
�S�D�R�@���ʕ��͂ɂ�����2�Q�̕ꕽ�ς̍��̌�������{
4.3.1�@�Q�P�̒��S����Q�Q�̒��S�܂ł̃}�n���m�r�X�̋��������߂�B
�Q�P�̒��S����Q�Q�̒��S�܂ł̃}�n���m�r�X�̋����c02��
![]()
�c02 ���@4.6049�~(5.25�|7)�{11.3601�~(7�|3.25)�|7.08042�~(4.25�|6.25)
���@48.7026 ���@48.703
4.3.2�@�Q�Q�̕ꕽ�ςɍ������邩�ǂ�����������{����B
�A�������F�g0�F��1����2 �i�Q�Q�̕ꕽ�ς͓������j
�Η������F�g1�F��1����2 �i�Q�Q�̕ꕽ�ς͓������Ȃ��j
���蓝�v�ʂ��e�Ƃ����
![]()
������
n1�F�Q�P�̕W�{���@n2�F�Q�Q�̕W�{���@p�F�ϗʐ� �c2�F������̋���
�����茟�蓝�v�ʂe�́A
![]()
�@
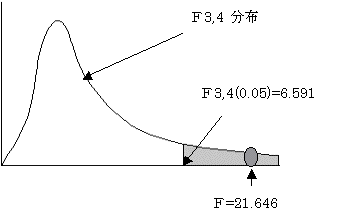
p=3 �ł��邩�� n1�{n2�|p�|1=4�{4�|3�|1=4 ���R�x 3,4 �̂e���z�ɏ]���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�e���e3,4(0.05) �ł���A���p��ɓ���B����ĂQ�Q�̕ꕽ�ς͓������Ƃ������������p����B�Q�Q�̕ꕽ�ςɍ�������B
�S�D�S�@�E�B���N�X�̃��i�����_�j���v�ʂ��g�p���āA�Q�Q�Ԃ̕ꕽ�ς̍��̎��{�B
�@�Q�P�i�`�ƊE�j�̂R�ϗʂ̕����a�E�Ϙa�s����r1�A�Q�Q�i�a�ƊE�j�̂R�ϗʂ̕����a�E�Ϙa�s����r2�A�Q���̐Ϙa�E�����a�s���rW�Ƃ���B
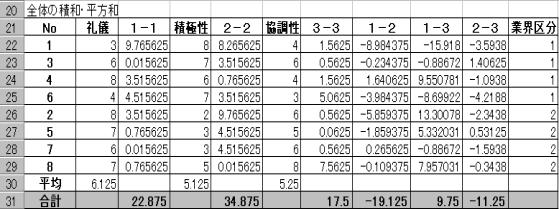
�ȏ���܂Ƃ߂��
�@�@�@
�b�rW�b��321.75
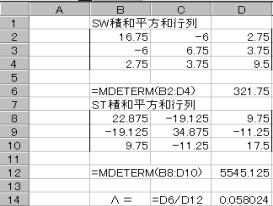
�S�̂̕����a�E�Ϙa�s��(�rT)
�@�@�@
�b�rT�b��5545.12
�ȏォ�烩���v�ʂ́A�����b�rW�b���b�rT�b
����321.75��5545.12��0.05802
���̎��Q�Q�̕ꕽ�ςɍ������邩�ǂ����̌��蓝�v�ʂe��
![]()
�������A���F�W�{�����W�@���F�ϗʐ����R
�����v�ʂ��狁�߂����蓝�v�ʂƁA�}�n���m�r�X�̋������狁�߂����蓝�v�ʂ͈�v����B
�S�D�T�@�딻�ʂ̊m��

�@
�W�����K���z�Ɋւ����
![]() �@�@�y�l����m�������߂�@�c�@=normsdist(Z�l)
�@�@�y�l����m�������߂�@�c�@=normsdist(Z�l)
�@�@�m������Z�l�����߂�@�c�@=normsinv(�m��)
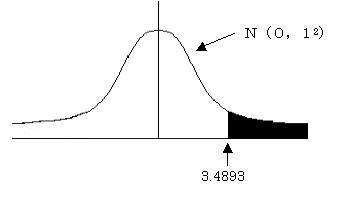
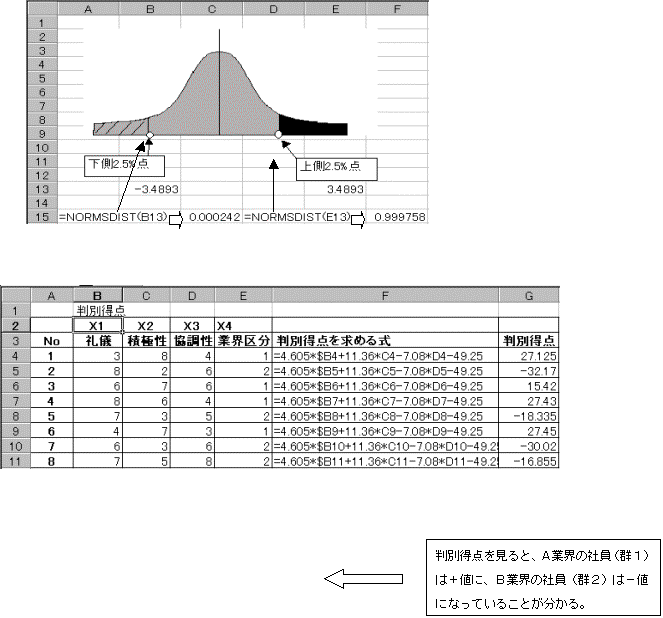
���ϑ����ꂽZ�l=3.4893�ł���B���̎��̊m���l�́@=normsdist(3.4893)=0.999758
�ƂȂ�B����͉��}�̊D�F�����̒l�i�|������3.4893�j�܂ł̊m���l�ł���A����Ɏg�p����㑤�m���l�́A1�|�@0.999758=0.000242�̒l���g�p����B���K���z�͋���ł��邩��A����2.5%��Z�l(�|3.4893)���g�p����A�����l�邱�Ƃ��ł���B=normsdist(3.4893)=0.000242
�딻�ʂ̊m����0.024%�ł��邱�Ƃ�������B
�S�D�U�@���ʓ��_�����߂�
���ʓ��_�́A���ʎ��@�x��4.605��w1�{11.36��w2�|7.08��w3�|49.25 �ŋ��߂�B
|
�ԍ� |
���ʓ��_ |
|
1 2 3 4 5 6 7 8 |
27.12 �|32.17 15.42 27.43 �|18.335 27.45 �|30.02 �|16.85 |
�S�D�V�@�悢���ʎ����쐬����B
�悢���ʎ��́A���Ȃ��ϗʂōŗǂ̔��ʌ��ʂ��锻�ʊ������߂邱�Ƃł���B
�ϐ������@�ōŗǂ̔��ʎ������߂�B
�ϐ������@�ł́A�g�p����ϐ������X�ɑ��₵�Ă������@�ł���B
�S.7.1�@�ŏ���3�ϗʂ̂����A���ʎ��ōł���^���Ă���ϗʂ��̗p����B�ł���^���Ă���ϗʂ͌��蓝�v��F�l�̍ł��傫�Ȓl��^����ϗʂł���B
�ϗʂ��P���g�p�������̃}�n���m�r�X�̔ċ��������߂�B
�u�ϗ�X1�̂ݎg�p�������̃}�n���m�r�X�̔ċ����v
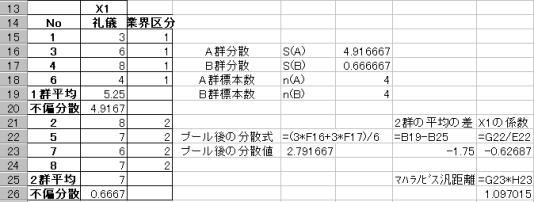
A�Q�EB�Q�̊e�s�Ε��U�����ŋ��߂�B�s�Ε��U�����߂���́@��VAR(�͈�)�ł���B
A�Q�EB�Q�̕W�{���͂Ƃ��ɂS�ł���B���ꂩ��v�|����̕��U�����߂�B

�@���l�ɂ��āAX2�ϗʂ݂̂��g�p�������AX3�ϗʂ̂ݎg�p�������̂��ꂼ��̃}�n���m�r�X�̔ċ��������߂�B�����쐬���Ă����AX2�̕ϗʂ��R�s�[��������ɍČv�Z����āAX2���g�p�������̃}�n���m�r�X�̔ċ��������߂���B
�u�ϗ�X2�̂ݎg�p�������̃}�n���m�r�X�̔ċ����v

�u�ϗ�X3�̂ݎg�p�������̃}�n���m�r�X�̔ċ����v

�ȏォ��e�ϗʂ��P�g�p���̃}�n���m�r�X�̔ċ�����
![]() �@�@�@X1�ϗʎg�p���̃}�n���m�r�X�̔ċ����F1.097
�@�@�@X1�ϗʎg�p���̃}�n���m�r�X�̔ċ����F1.097
�@�@�@X2�ϗʎg�p���̃}�n���m�r�X�̔ċ����F12.5
�@�@�@X3�ϗʎg�p���̃}�n���m�r�X�̔ċ����F2.526
�e�ϗʂP�g�p�������̌W�������ɗ����̌��蓝�v��F��
�@�@�@![]()

![]() �@�@ X1�ϗʎg�p����F�l�F2.194
�@�@ X1�ϗʎg�p����F�l�F2.194
�@�@ X2�ϗʎg�p����F�l�F25
�@�@ X3�ϗʎg�p����F�l�F5.053
���ꂼ��̊e�ϗʂ��P�g�p���ē���ꂽ���`���ʎ��̂e�l�ōő�̂e�l��^����̂́A�ϗʂw2���g�p�������ł���̂ŁA�܂��ϗʂw2���̗p����B

���̎��̂Q�Q�̒��S�Ԃ̃}�n���m�r�X�̋�����12.5�ł���̂ŁA���ꂩ��ϗʂw2�������g�p�������̐��`���ʎ��Ŕ��ʂ����Ƃ��A���̌W�������ɗ����ǂ������肷��B
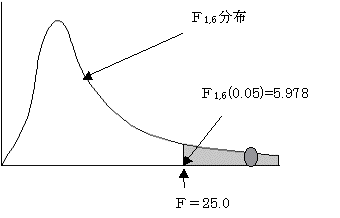
���蓝�v�ʂ��e�Ƃ���Ƃe��25.0
���R�x�́A1,4�{4�|1�|1=6 �ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@
�L�א�����=0.05��
�e=25.0 ��
�e1,6(0.05)=5.978 �ł��邩��A�W����2���O�ł���B
4.7.2�@�Q�Q�̑��֔�����߂āA���֔�̌�����s���B
���܍��i�Q�E�s���i�Q�ɌQ��������ƈȉ��̂悤�ȕ\�ɂȂ�B
|
|
�m�n |
�w1 |
�w2 |
�w3 |
|
�� �e �Q |
�P �R �S �U |
�R �U �W �S |
�W �V �U �V |
�S �U �S �R |
|
�s �� �e �Q |
�Q �T �V �W |
�W �V �U �V |
�Q �R �R �T |
�U �T �U �W |
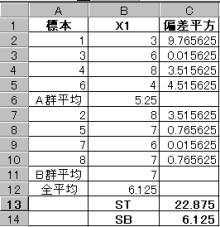
�ϗʂw1�ɂ��č��i�Q�E�s���i�Q�ɕ������
|
|
�m�n |
�w1 |
|
�� �e �Q |
�P �R �S �U |
�R �U �W �S |
|
�s �� �e �Q |
�Q �T �V �W |
�W �V �U �V |
�S�ϓ����rT�A�Q�Q�Ԃ̋��ԕϓ����rB�Ƃ����
�rT��22.875 �rB�� 4�~(5.25�|6.125)2 �{ 4�~(7�|6.125)2 =
6.125
����ă�2���rB���rT��0.26776
![]()
F=2.194�̎��̊m���l�́A��FDIST(F�l�A���R�x1�A���R�x2)���狁�߂�B
�����R�x1�F1�@�@���R�x2�F6�ł��邩��
|
F�l |
F�l�� |
�m�� |
|
2.194 |
=FDIST(E2,1,6) |
0.189054 |
|
25 |
=FDIST(E3,1,6) |
0.002452 |
|
5.053 |
=FDIST(E4,1,6) |
0.065631 |
���l�ɕϗʂw2�ɂ��č��i�Q�E�s���i�Q�ɕ����A�S�ϓ��E���ԕϓ������2��0.80645�ł��邩��e��25�B�ϗʂw3�ɂ��č��i�Q�E�s���i�Q�ɕ����A�S�ϓ��E���ԕϓ������2��0.457143
�@�e��5.053�@�Ƌ��߂���B
�S.7.3 �ϗʂw2���̗p�����̂ŁA���ɕϗʂ��P���₵�Ăe�l����������B
�@�ϗʂ����������A���̕ϗʂ��̗p���邩�ǂ����̖ڈ��Ƃ��āAF�l�����߁A���̒l��2�ȏ�ł���̗p����悤�ɂ���B
(�P)�ϗʂw2�ɕϗʂw3����������
���`���ʎ��́A�x=5.1685��w2�|3.30337��w3�|9.14607
���̎��̂Q�Q�̒��S�Ԃ̃}�n���m�r�X�����́A25.989�ł���B
���̐��`���ʎ��̕ϗʂw3�̌W����3�����ʂɖ𗧂��ǂ�����������{����B
��3���O�i�ϗʂw3�̌W����3�͖��ɂ����Ȃ��j�Ƃ��������̂��Ƃ�
���蓝�v�ʂ��e�Ƃ����
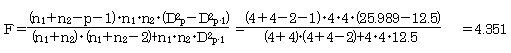
�ϗʂw2���g�p�������`���ʎ��ŁA�Q�Q�ɔ��ʂ����Ƃ��̂Q�Q�̒��S�Ԃ̃}�n���m�r�X�̋����͂c2 ��12.5�B�ϗʂw2�Ƃw3���g�p�������`���ʎ��ŁA�Q�Q�ɔ��ʂ����Ƃ��̂Q�Q�̒��S�Ԃ̃}�n���m�r�X�̋�����
�c2 ��25.989
F�l:4.351�ł���̂ŁAX2�ɕϗ�X3�����������͍̗p����B
(�Q)�ϗʂw2�ɕϗʂw1����������
���`���ʎ��́A�x=0.832117��w1�{4.07299��w2�|0.259708
���̎��̂Q�Q�̒��S�Ԃ̃}�n���m�r�X�����́A13.818�ł���B
���̐��`���ʎ��̕ϗʂw1�̌W����1�����ʂɖ𗧂��ǂ�����������{����B
��1���O�i�ϗʂw1�̌W����1�͖��ɂ����Ȃ��j�Ƃ��������̂��Ƃ�
���蓝�v�ʂ��e�Ƃ����
![]()
�ϗʂw2���g�p�������`���ʎ��ŁA�Q�Q�ɔ��ʂ����Ƃ��̂Q�Q�̒��S�Ԃ̃}�n���m�r�X�̋����͂c2 ��12.5�B�ϗʂw2�Ƃw1���g�p�������`���ʎ��ŁA�Q�Q�ɔ��ʂ����Ƃ��̂Q�Q�̒��S�Ԃ̃}�n���m�r�X�̋�����
�c2 ��13.818
F�l:0.425�ł���̂ŁAX2��X1�̕ϗʂ����������͍̗p���Ȃ��B
�ȏ�̕ϐ������@�ɂ��ŗǂ̐��`���ʎ��́A�x=5.1685��w2�|3.30337��w3�|9.14607�ł���B
�S�D�W�@���߂��d��A�����g�p���A���m�̒l��\������B
�@�@���܂`�ƊE�E�a�ƊE�̋ƊE�敪�s���̐l���K��Ă������A���̐l�̈�ۂ��A
�w1�i��V�j���U�@�w2�i�ϋɐ��j���T�@�w3�i�������j���U �ł������Ƃ���Ƃ��̐l�͂`�ƊE�E�a�ƊE�̂ǂ���̐l�ł���Ɣ��ʂł��邾�낤���H
�R�ϗʂ��g�p�������̐��`���ʎ����g�p�����
�@���`���ʎ��́A�x��4.6049��w1�{11.3601��w2�|7.08042��w3�|49.2635
�@�@�x��4.6046�~6�{11.3601�~5�|7.08042�~6�|49.2535 = �|7.30792
����āA�a�ƊE�̎Ј��ƍl������B
�ϐ��I��@�ŋ��߂��A�ŗǂ̐��`���ʎ����g�p�����
���`���ʎ��́A�x=5.1685��w2�|3.30337��w3�|9.14607 �ł��邩��A
�x��5.1685�~5�|3.30337�~6�|9.14607= �|3.12379
����āA�a�ƊE�̎Ј��ƍl������B