ホームへ戻る

３．判別分析

　２群以上の母集団から抽出した標本データを得て、いまどの母集団に属するか不明のサンプルデータがあるとする。このサンプルデータがどの母集団に属するか調べる方法に、判別分析がある。判別分析を実施するには、集めた標本がどの母集団に属しているのかをあらかじめ区分けしておく必要がある。区分けする方法に、線形判別式を使用する方法と、マハラノビスの距離を用いる方法がある。

３．１　線形判別式を使用する方法

　多変量データｘ₁･ｘ₂…ｘ_n があるとする。この説明変量ｘ₁･ｘ₂…ｘ_n  はいずれも量的データであり、この変量に適当な重みａ₁･ａ₂…ａ_n をつけ目的変量Ｚを得る。

   Ｚ＝ａ₁･ｘ₁＋ａ₂･ｘ₂＋…＋ａ_n･ｘ_n＋ａ₀

 この時得られる目的変量Ｚが区分わけを示す質的データであるとき、この式を線形判別式という。重回帰式では、説明変量も目的変量も量的データを扱ったが、判別分析においては、説明変量は量的データであるが、得られる目的変量はどの母集団に属するのか示す質的データを扱う。

　いま、Ａ中学校の８人の生徒の英語（ｘ₁）と数学（ｘ₂）の評価があり、この８人の生徒がＢ高校を受験してその合否結果（Ｚ）が分かっているとする。すると、ここに２つの母集団、合格群と不合格群があることになる。

NO	説明変量 英語(ｘ1)　　数学(ｘ2)	目的変量（Ｚ） 合　否
１ ２ ３ ４ ５ ６ ７ ８	５　　　 ８ ５ 　　　５ ７       ４ ８       ５ ７       ２ ４       ３ ８       ７ ４       ６	合 否 合 合 否 否 合 否
平均	６       ５

  

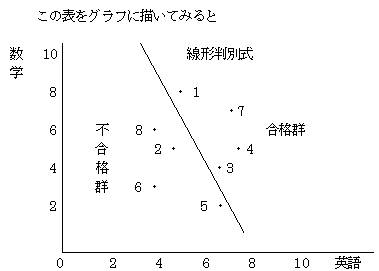
合格した群（１･３･４･７）と不合格の群（２･５･６･８）を区分わけする直線を１本考える。

 この直線が、線形判別式となる。この線形判別式が判明すれば、どの母集団に付属するのか不明のサンプルデータの所属を得ることができる。

3.1.1　線形判別式を求める。

　説明変量が２つあるのでこれをｘ₁・ｘ₂ とすると、この判別式を

　　　　Ｚ＝ａ₁･ｘ₁＋ａ_2･ｘ₂＋ａ₀   とする。

　合格した群をＡ群、不合格の群をＢ群とすると、この判別式Ｚは、２群（Ａ群とＢ群）から最も遠い位置に引かれる必要がある。２群から最も遠い位置に引かれることにより、この判別式は、２群Ａ・Ｂを区分けする最も良い基準線となる。

　　

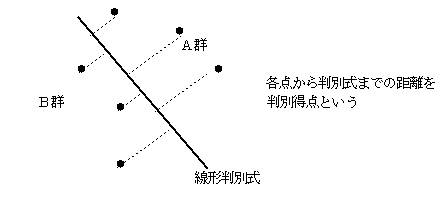
（１）判別得点を求める

　　　判別得点は、各標本データ点から判別式までの距離で表される。

　　　もとの標本を合格した群と不合格の群に分けて整理すると

 

NO	説明変量 英語(ｘ1)   数学(ｘ2)	目的変量（Ｚ） 合　否
１ ３ ４ ７	５         ８ ７         ４ ８         ５ ８         ７	合 合 合 合	A   群
平 均	７         ６
２ ５ ６ ８	５         ５ ７         ２ ４         ３ ４         ６	否 否 否 否	B   群
平 均	５         ４
全平均	６         ５

 

説明変量ｘ₁･ｘ₂は量的データであり、目的変量Ｚは区分を示す質的データである。

通常量的データ間の関係を表すものとしては相関係数があるが、量的データと質的データの関係を表すものとして相関比（η）がある。相関比（η）は

         η²＝級間変動÷全変動  で与えられる。

 

   それぞれの標本について判別得点を求める。

　　　

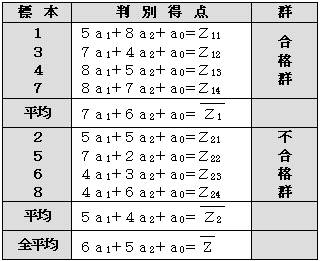
 ２群を最もよく分けるには、全変動をＳ_T 級間変動をＳ_Bとするとき、相関比（η²）を最大にするようにする。

  全変動Ｓ_Tは、全平均Ｚから各々のデータがどれ位散らばっているかである。

 

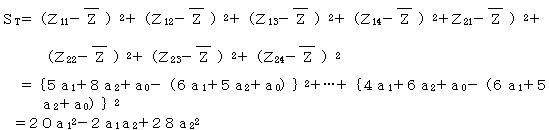
  級間変動Ｓ_Bは、Ａ群の平均が全平均からどの位散らばっているかと、Ｂ群の平均が全平均からどの位散らばっているかを合計したものである。

　　　　　　　　　　　　

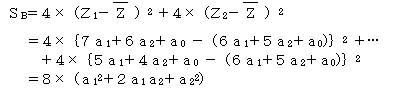
（２）相関比を求める

ｔ＝1.381,−1　で相関比η2は最大値または最小値を持つ。このｔの値を相関比η²に代入するとｔ＝−1の時 η²＝０　となり最小となる。ｔ＝1.381の時  η²＝0.71556　となり最大となる。つまり相関比η²は、ａ₁÷ａ₂＝−1の時最小となり、ａ₁÷ａ₂＝1.381の時最大となる。いま求めようとしているのは、相関比η²を最大とするａ₁･ａ₂であるから、1.381を採用する。

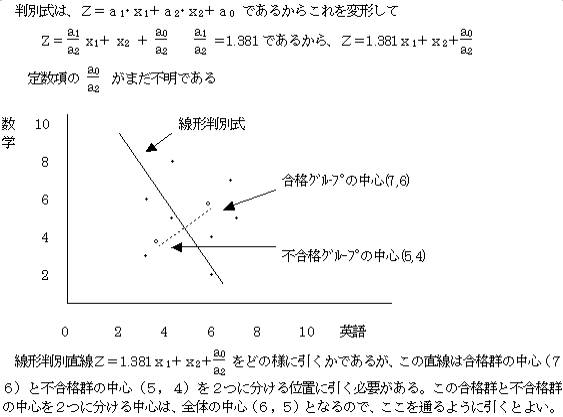
これより求める線形判別式は、Ｚ＝1.381ｘ₁＋ｘ₂−13.286 となる。この線形判別式を使用することにより、データを２群に分けることができる。

      実際に判別得点を求めて表にしてみると

 

　　　

 

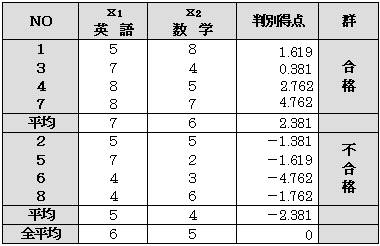
      判別得点を見ると、合格群は＋　不合格群は−に群分けされていることが分かる。

　　　以上から、グラフを描いてみると

 

 

 

 

 

 

 

 

 

 

 

 

 

 

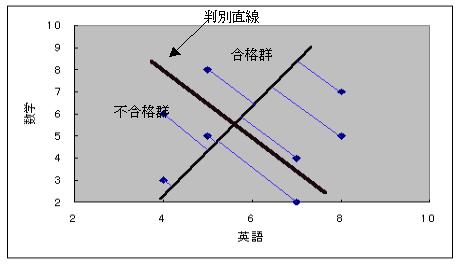
　判別直線を境にして、右側に合格群、左側に不合格群があることが分かる。

  また全平均（６、５）を通り判別直線に直行する直線を１本引き、その直線上に各点から降ろした点を見ると、全平均（６、５）を新たな原点と考えると上側（＋側）に合格群、下側（−側）に不合格群がありその距離が判別得点となっていることが分かる。

 

3.1.2　分散・共分散行列を用いて判別式を求める。（不偏分散を使用する）

（１）説明変数が２個の時

   判別式 Ｚ＝ａ₁･ｘ₁＋ａ₂･ｘ₂＋ａ₀  を求めるのに分散共分散行列を利用して求める方法がある。いま説明変量がｘ₁･ｘ₂と２つあり、Ａ群･Ｂ群の２群に分かれている。

 

　　　

    

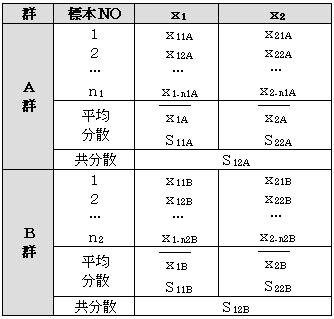
 いまＡ群・Ｂ群が上の様になっているとき

 

 

 

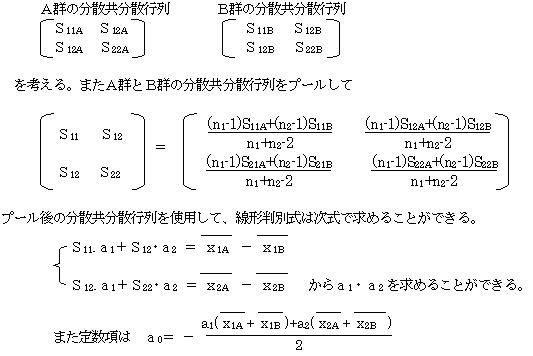
（２）説明変量がｐ個ある時に２Ａ群・Ｂに分けるとき

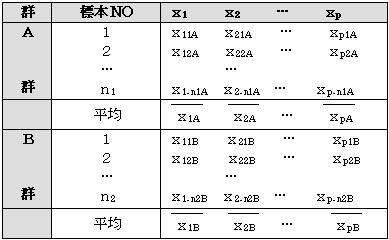
    この時、Ａ群の分散共分散行列をＳ_A、Ｂ群の分散共分散行列をＳ_B　

　　プール後の分散共分散行列をＳとすると

   

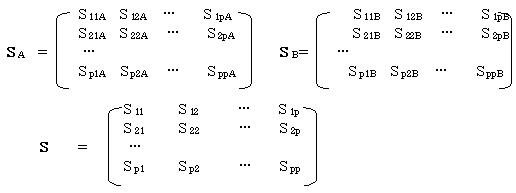
３．２　ボックスＭ検定

　線形判別式を使用して２群を区分わけできるのは、母分散共分散行列が等しい時に限られる。２群の母分散が等しい時には、その判別式は直線になるが、等しくない時には判別式は曲線となる。母分散共分散行列が等しくない時には、マハラノビスの距離による判別を行う必要がある。母分散共分散行列が等しいかどうかの検定に「ボックスＭ検定」がある。

「ボックスＭ検定」

  Ａ群・Ｂ群のそれぞれの分散共分散行列をＳ_A・Ｓ_Bとする。またＳ_A・Ｓ_Bのプール後の分散共分散行列をＳとすると

 

 

       p：説明変量の個数　ｎ_A：Ａ群の標本数  ｎ_B：Ｂ群の標本数

 

   自由度　ｐ（ｐ＋１）／２のχ² 分布に漸近的に従う。これを利用して検定を行う。

 (1)仮説をたてる

　 帰無仮説　Ｈ₀ ：２群の母分散共分散行列は等しい

　 対立仮説　Ｈ₁ ：２群の母分散共分散行列は等しくない

 (2)検定統計量χ2は自由度ｐ（ｐ＋１）／２のχ² 分布に従う。

 (3)有為水準をαとすると

 

 

 

 

 

 

 

 

 

 

                           　　　

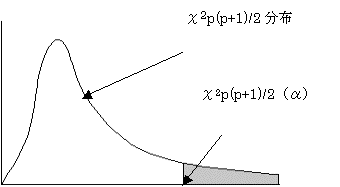
 χ² ＞ χ²_p(p+1)/2（α）であれば仮説を棄却する。つまり、２群の母分散共分散行列は等しくない。よってマハラノビスの距離による判別処理をする方が望ましい。

３．３　マハラノビスの距離による判別

3.3.1　マハラノビスの距離

（１）１変量時のマハラノビスの距離

 

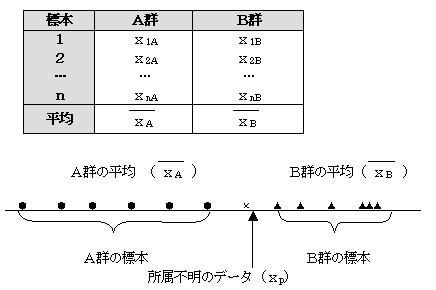
 １変量のデータＡ群とＢ群が上の様に分布しているとする。Ａ群のデータは分散の大きいデータ群、Ｂ群のデータは分散の小さいデータ群である。この時所属不明のデータｘ_pがある時、この所属不明のデータｘ_pがＡ群、Ｂ群のどちらに所属するデータであるか調べる

 　単純にｘ_pからそれぞれの群の中心までの距離を見ると、明らかにこのｘ_pはＢ群の中心に近い。となっていので、このｘ_pはＢ群のデータであるように思える。しかしＡ群は分散の大きいデータ群であり、Ｂ群は分散の小さいデータ群である。この分散を考慮しないで、単純に距離だけでどちらの群に所属するのかを判断することはできない。この分散を考慮した距離に「マハラノビスの距離」がある。

１変量時のマハラノビスの距離をＤ²とすると、

　　　

  このように分散を考慮すれば、分散の大きいデータほどマハラノビスの距離は小さくなり、　逆に分散の小さいデータほどマハラノビスの距離は大きくなる。

 

    Ｄ_A²＜Ｄ_B² であればｘpは、Ａ群に近い。Ｄ_A²＞Ｄ_B²であればｘ_pは、Ｂ群に近い。

（２）２変量時のマハラノビスの距離

        ２変量のデータがＡ群・Ｂ群の２群に分かれているとする。

 

 

 

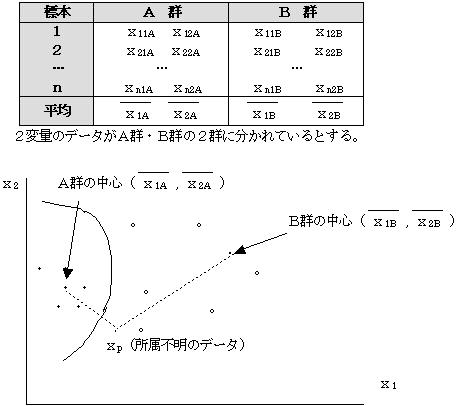
 Ａ群は分散の小さいデータ群、Ｂ群は分散の大きいデータ群とする。この時所属不明のデータｘ_p（ｘ₁,ｘ₂）がある時、このデータｘ_pはＡ群・Ｂ群のどちらに所属するデータであるか調べる。

  単純な距離を考えると、ｘ_pからＡ群への距離はであり、ｘ_pからＢ群への距離は  である。一見してこのデータｘ_pは、Ａ群に近そうである。しかしＡ群は分散の小さいデータ群であり、Ｂ群は分散の大きいデータ群であるので、分散を考慮しない単純な距離だけでは判断することはできない。次に、分散を考慮したマハラノビスの距離を考えると

　　　

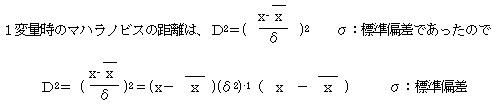
これを２変量について考えと、  １変量から２変量になったので

 

 

 

 

 

 同様にして変量ｐ個の時のマハラノビスの距離は

 

 

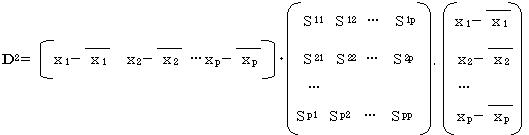
  マハラノビスの距離は、各群の中心からその標本への分散を考慮した距離を示すので、その標本はマハラノビス距離の小さい方の群に所属する標本であるとする。

３．４　多変量における２群の母平均の差に関する検定

3.4.1　２群間の母平均に差があるかどうか検定を行う。

 いま２群がそれぞれＮ（μ₁，σ²）・Ｎ（μ₂，σ²）に従うとき、ここからｎ₁個・ｎ₂個の標本を得たとする。この時２群の母平均μ₁＝μ₂であるかどうか検定は

 　検定統計量をＦとすると

　　　　　

      ただしｐ：説明変量の個数　Ｄ²：２群の中心間のマハラノビスの汎距離

　は自由度ｐ，ｎ₁＋ｎ₂−ｐ−１のＦ分布に従う。これを利用してｐ変量の２群の母平均の差の検定を行う

(1)仮説をたてる

　 帰無仮説  Ｈ₀：μ₁＝μ₂  （２群の母平均は等しい）

　 対立仮説  Ｈ₁：μ₁≠μ₂  （２群の母平均は等しくない）

(2)検定統計量Ｆは自由度ｐ，ｎ1＋ｎ2−ｐ−１のＦ分布に従う

(3)有為水準αで検定をおこなう

 

 

 

 

 

 

 

 

 

 

 

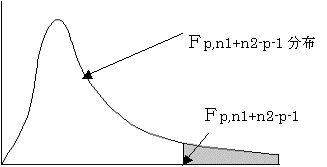
   Ｆ＞Ｆp,n1＋n2−p−1（α）であれば仮説Ｈ0を棄却する。つまり２群の母平均に差があるとする。

 

 

 

 

 

3.4.2　ウィルクスのΛ（ラムダ）統計量

      多変量時の群間の変動を示す量として、ウィルクスのΛ統計量がある。

　　  ２群の多変量データが下の表のようにあるとすると

群	変量 標本	Ｘ1   　  Ｘ2   　  …　　Ｘp
Ａ   群	１ ２ … ｎ1	Ｘ11A   Ｘ21A    …　  Ｘp1A Ｘ12A   Ｘ22A    …　  Ｘp2A … Ｘ1･n1A Ｘ2･n1A  …　  Ｘp･n1A
Ｂ   群	１ ２ … ｎ2	Ｘ11B   Ｘ21B    …　  Ｘp1B Ｘ12B   Ｘ22B    …　  Ｘp2B … Ｘ1･n2B Ｘ2･n2B  …    Ｘp･n2B

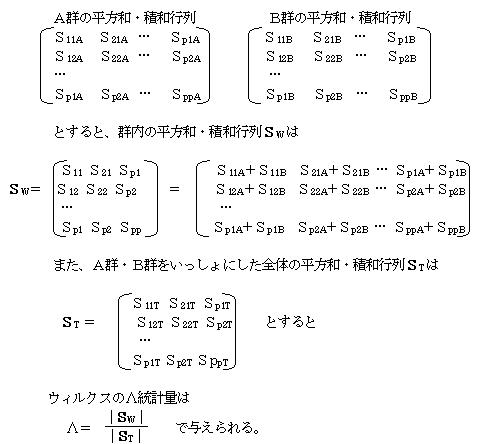
 Λ統計量は、０≦Λ≦１の値をとり、Λが０に近いほど２群間の差が大きく、Λが１に近づくほど２群間の差が小さくなる。

 このΛ統計量を使用して、２群間の母平均の差の検定をすることができる。

 ２群ｐ変量の母平均をそれぞれμ_iA・μ_iBとすると、μ_iA＝μ_iBの仮定下で

      検定統計量をＦとすると、

　　　　　　

 上記検定統計量Ｆを使用して、有為水準αで仮説Ｈ0：μ_iA＝μ_iB  i=1,2…p を検定し、もしＦ≧Ｆp,n−p−1（α）であれば仮説を棄却し、２群の母平均に差があるとする。

３．５　判別分析の的中率

　判別分析を実施して所属する群を判別したとき、その標本が本当に所属している母集団と正しく判定されたかどうかの精度を計るものに判別的中率がある。

  判別的中率＝（正しく判別された標本÷全標本の数）×１００ である。             

３．６　誤判別の確率

　母集団が２つある時、ある標本を間違った母集団からの標本であると判定する誤りの確率を誤判別の確率という

  標本が２Ａ群・Ｂに分かれており、その説明変量がｐ個ある時、Ａ群の説明変量の平均をｘ_1A・ｘ_2A…ｘ_pA、またＢ群の説明変量の平均をｘ_1B・ｘ_2B…ｘ_pB とする。この時、Ａ群の中心からＢ群への中心へのマハラノビスの距離Ｄ₀² は

  

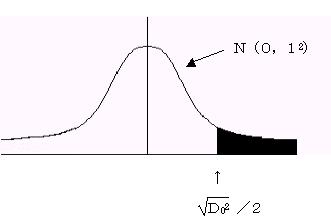
は標準正規分布Ｎ（０，１2）に従うので、これから誤判別の確率を求める。

 いまＰ₁をＡ群の標本であるにもかかわらず、Ｂ群の標本であると判定する間違いの確率。 またＰ₂をＢ群の標本であるにもかかわらず、Ａ群の標本であると判定する間違いの確率とすると誤判別の確率は、Ｐ₁＝Ｐ₂＝標準正規分布の値の上側確率である。

　　　　　　　

　　        　　　　　　　                                  

３．７　説明変量の寄与

　線形判別式を、Ｚ＝ａ₁ｘ₁＋ａ₂ｘ₂＋…＋ａ_nｘ_n＋ａ0とする。この時係数ａiが、判別式に寄与しているかどうか調べる。もし寄与していないのであれば、その説明変量はなくても判別結果に影響を与えていないので、線形判別式から落としてもよい係数である。

 ２Ａ群・Ｂで説明変量がｐ個ある時、下の表のようであるとする。

 

群	標本NO	ｘ1    　  ｘ2        …     ｘp
Ａ 群	１ ２ … ｎ1	ｘ11A    ｘ21A    …     ｘp1A ｘ12A    ｘ22A    …     ｘp2A … ｘ1･n1A  ｘ2･n1A  …     ｘp･n1A
Ｂ 群	１ ２ … ｎ2	ｘ11B    ｘ21B  　…     ｘp1B ｘ12B    ｘ22B    …     ｘp2B … ｘ1･n2B  ｘ2･n2B  …     ｘp･n2B

 

  Ｄ²_P：Ｐ個の変量を使用した２群の中心間のマハラノビスの距離。Ｄ²_P-1：Ｐ個の変量からある特定の変量を１つ落としたときの２群の中心間のマハラノビスの距離 とすると   

のでこれを利用して係数の有用性の検定を行う。

検定を行う

 (1)仮説をたてる

　　帰無仮説　Ｈ₀：ａ_i＝０　（係数ａiは役にたたない）

    対立仮説  Ｈ₁：ａ_i≠０

(2)検定統計量Ｆは自由度１，ｎ₁＋ｎ₂−ｐ−１のＦ分布に従う。

 

(3)有為水準αで検定を行う

 

 

 

 

 

 

 

 

        　　　　　　　　　　　　　　　　                    

 

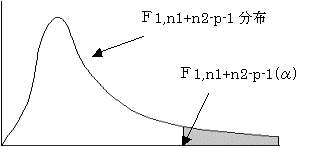
  Ｆ＞Ｆ1,n1＋n2−p−1(α)であれば、仮説Ｈ₀を棄却する。つまり係数ａiは判別式に寄与しているといえる。

  判別式に寄与していない係数は、使用しなくても結果に影響を与えていないので不必要な変量であるといえるので、その係数は削除しても構わない。

　この係数の寄与についてのＦ値を使用することにより、重回帰式と同様に変数選択の前進選択法・後退減少法ならびに変数増減法などの変数選択を実行することができる。

３．８　よい判別式を作成する。

　判別式では、いくつかの量的データである説明変量から区分わけを示す質的データである目的変量を得る。この時重回帰式と同様に説明変量をむやみに多くしても無駄なことが多い。よい判別式は、少ない説明変量で精度の高い区分わけができるような式である。このために説明変量を調べ、判別式に必要な変量であるかどうか検討する必要がある。

 

 

3.8.1　説明変量選択の基準

（１）目的変量に与える影響の大きい説明変量を選ぶ。

　重回帰分析では、説明変量・目的変量ともに量的データであるので、その関係は相関係数で調べることができたが、判別分析では説明変量は量的データで目的変量は質的データで　　　ある。このように量的データと質的データ間の関係を調べるには相関比（η）を使用する。

  なお、相関比（η）は、０≦η≦１の値をとり、１に近いほど級間変動が大きく２変量間の関係が強いといえる。

　いま説明変量がいくつかあり、その中の１つの変量ｘが２Ａ群・Ｂに分かれているとする。この時の相関比を求める。

　　　　　

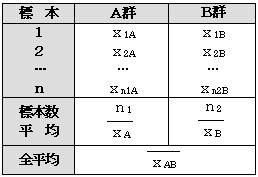
 相関比の２乗（η²）は η²＝級間変動÷全変動  で与えられる。

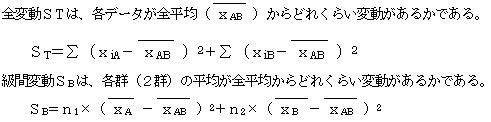
これから相関比（η²）＝Ｓ_B÷Ｓ_Tが求められる。

 各変量について相関比を求め、相関比の大きい変量ほど目的変量に与える影響が大きいといえるので積極的に判別式に採用する。

 

  ［相関比に関する検定］

    変量ｘ₁…ｘ_pがお互いに独立であり、ともに正規分布に従うものとする。

    (1)仮説をたてる

　　　 帰無仮説  Ｈ₀：η₀＝０    （母相関比＝０）

　　　 対立仮説  Ｈ₁：η₀≠０    （母相関比≠０）

 

  (2)検定統計量をＦとする

   

 

 

  (3)有為水準αで検定する

 

 

 

 

 

 

 

 

 

 

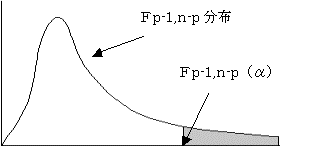
   Ｆ≧Ｆp−1,n−p（α）であれば、仮説を棄却する。つまり母相関比≠０とする。

（２）説明変量間でお互いに高い相関がある時には、どちらかの変量を落とす。説明変量間の相関については、単相関係数を用いて調べる。これは重回帰式と同様に説明変量間でお互いに高い相関があるときには、多重共線性を示すからである。お互い高い相関がある変量は、同じことを説明しているので、どちらか一方の変量を落としても目的変量に与える影響は小さく、判別結果に差異はないといえる。

 

 「係数ａiの符号」と「２群の平均の差の符号」を見れば、多重共線性が分かる。

3.8.2　判別式における変数選択法

　重回帰式の時と同様に、判別式においても説明変量選択の方法がある。　　

　説明変量の選択の方法には、重回帰式同様「変数増加法」「変数減少法」「変数増減法」「変数減増法」などがあり、これらの方法を重回帰式の時と同じように行う。

  変量採否の基準としては、説明変量の寄与での係数ａiのＦ値を検討しながら行う。